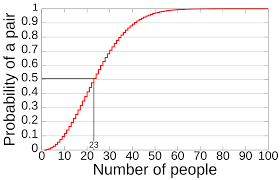
생일 문제(birthday problem)는 확률론에서 "n명의 무작위로 선택된 사람들 중에서, 적어도 두 명이 같은 생일을 가질 확률" 을 묻는 고전적인 문제다. 이 문제는 1927년경 수학자 해럴드 데이븐포트(Harold Davenport)에게 귀속되지만, 그는 이를 출판하지 않았고, 실제로는 1939년 리하르트 폰 미제스(Richard von Mises)가 처음으로 관련 내용을 출판했다. 문제의 본질은, 우리의 직관과 달리 23명만 모여도 두 사람이 같은 생일을 가질 확률이 50%를 넘는다는 점에서 "생일 역설(birthday paradox)"이라고도 불린다.
birthday problem 시뮬레이션 코드 예시
파이썬을 이용한 대표적인 생일 문제 시뮬레이션(몬테카를로 실험) 코드는 아래와 같다. 이 코드는 여러 번 무작위로 n명의 생일을 생성하고, 그 중 두 명 이상이 같은 생일을 갖는 경우의 비율을 계산한다.
import random
def generate_birthdays(num_people):
# 1~365 사이의 무작위 생일 생성
return [random.randint(1, 365) for _ in range(num_people)]
def has_duplicate(birthdays):
# 중복 생일이 있는지 확인
return len(birthdays) != len(set(birthdays))
def birthday_simulation(num_people, num_trials):
match_count = 0
for _ in range(num_trials):
birthdays = generate_birthdays(num_people)
if has_duplicate(birthdays):
match_count += 1
return match_count / num_trials
# 예시: 23명이 모였을 때 10,000번 실험
probability = birthday_simulation(23, 10000)
print(f"23명 중 두 명 이상이 같은 생일을 가질 확률: {probability:.2%}")이 코드는 23명이 모였을 때 약 50%의 확률을 보여준다.
birthday problem이 시사하는 바
1. 인간의 직관과 확률의 괴리
- 대부분의 사람들은 366일(윤년 포함)이 있으니 183명쯤 모여야 50% 확률이 되지 않을까 생각하지만, 실제로는 23명에서 이미 50%를 넘는다.
이는 "쌍(pair)"의 수가 기하급수적으로 늘어나기 때문인데, 23명이면 253쌍이 만들어진다. 각 쌍마다 생일이 같을 확률이 누적되어 전체 확률이 빠르게 증가한다.
2. 암호학적 응용: Birthday Attack
- 해시 함수에서 충돌(collision)을 찾는 데 필요한 시도 횟수가 해시값의 비트 수 에 대해 에 불과하다는 점을 보여준다. 즉, 128비트 해시라면 번만 시도해도 충돌을 찾을 확률이 50%에 달한다. 이를 "생일 공격(birthday attack)"이라고 부르며, 해시 함수의 안전성 평가에 매우 중요한 의미를 가진다.
3. 비둘기집 원리(Pigeonhole Principle)의 직관적 예시
- 366명 이상이 모이면 반드시 생일이 같은 두 명이 존재한다는 점은 비둘기집 원리의 대표적인 예시다.
4. 실제 확률 계산 공식
- $$ n $명의 사람 중 적어도 두 명이 생일이 같을 확률 $ p(n) $$은 다음과 같다:
- 23명: 약 50.7%
- 57명: 약 99%
- 70명: 약 99.9%.
요약
생일 문제는 확률에 대한 인간의 직관이 얼마나 틀릴 수 있는지, 그리고 이로부터 파생되는 실질적(특히 암호학적) 시사점을 잘 보여주는 고전적 예시다. 간단한 파이썬 시뮬레이션으로도 이를 직접 실험해볼 수 있으며, 이 문제는 해시 함수의 충돌 가능성, 데이터 집합 내 중복 검출 등 다양한 분야에 응용된다.
Citations
[1] https://en.wikipedia.org/wiki/Birthday_problem
[2] https://ko.wikipedia.org/wiki/%EC%83%9D%EC%9D%BC_%EB%AC%B8%EC%A0%9C
