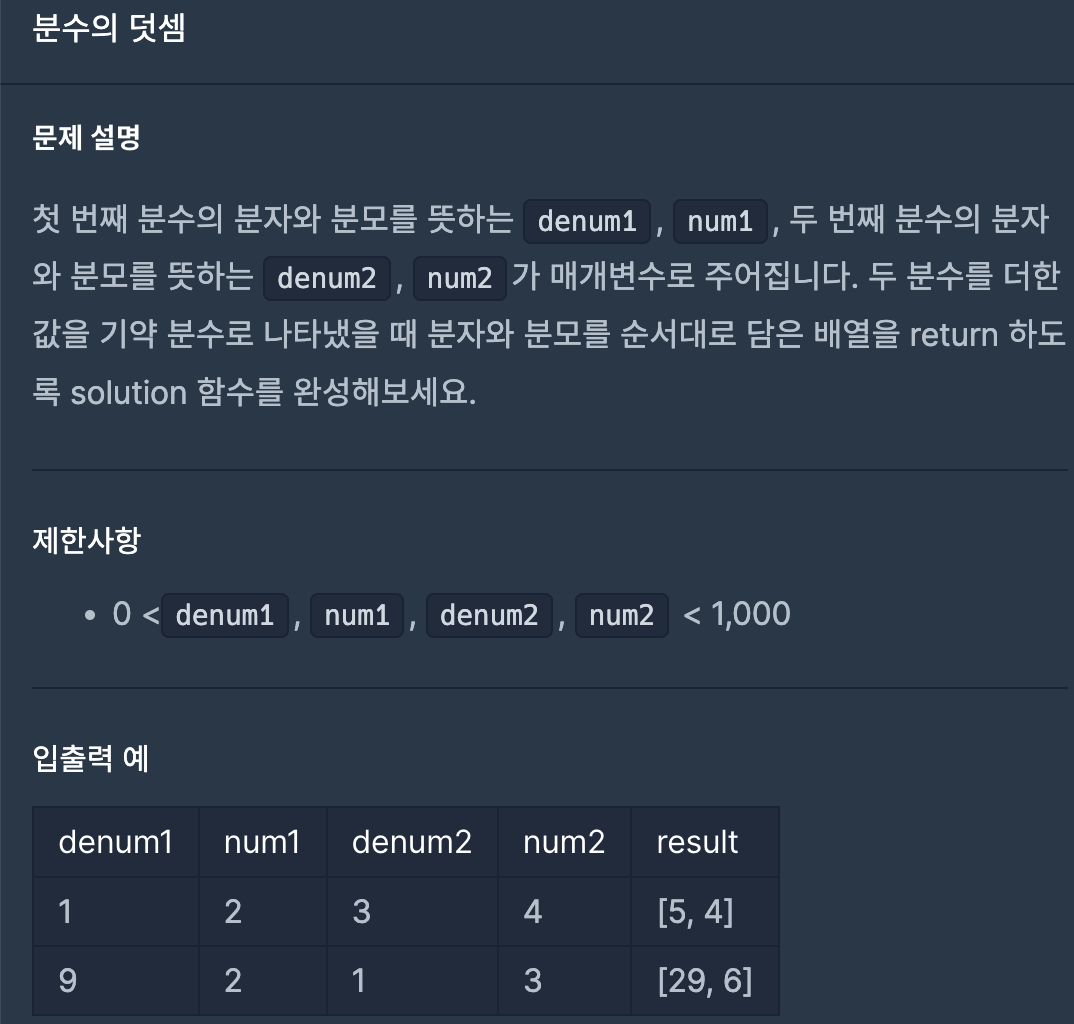
문제
코드
import java.util.Arrays;
class Solution {
public int[] solution(int denum1, int num1, int denum2, int num2) {
int[] answer = new int[2];
int top = (denum1 * num2) + (denum2 * num1);
int bottom = num1 * num2;
int divisor = gcd(top, bottom);
answer[0] = top / divisor;
answer[1] = bottom / divisor;
return answer;
}
public static int gcd(int a, int b) {
if (a <= b) {
int temp = a;
a = b;
b = temp;
}
if (b == 0) return a;
return gcd(b, (a % b));
}
}리뷰

레벨 측정이 잘못된 문제인건지 간단한 방법이 있는지는 잘 모르겠지만
유클리드 호제법이라는 알고리즘을 구현하여 풀어보았다.
반복문을 통해 간단하게 출력할 수 있겠지만 숫자가 크다거나 하면 시간복잡도도 높게 나올 듯 하고
여러 알고리즘을 공부해야 나중에 문제를 풀 때 다양한 시각으로 접근할 수 있을 것 같았다.
유클리드 호제법 (위키에 언어별 코드도 있었다.. 😳)
증명을 세세하게 하기에는 너무 길어질 것 같아 정리만 하자면
두 양의 정수 a, b (a > b) 에 대하여 a = bq + r (0 ≤ r < b) 이라 하면,
a, b의 최대공약수는 b, r의 최대공약수와 같다.
즉, gcd(a, b) = gcd(b, r) r=0이라면, a, b의 최대공약수는 b가 된다.
알고리즘을 공부하려다 수학을 공부하게 되었다 😅
유클리드 호제법을 이용하여 재귀함수를 구현해서 최대공약수를 구하고
계산한 분자와 분모를 최대 공약수로 나누어 배열에 담아 결과를 반환하였다.