빅오 표기법 (Big O Notation)

본 포스팅은 Colt Steele의 JavaScript 알고리즘 & 자료구조 마스터클래스를 수강하며 정리한 노트입니다.
https://www.udemy.com/course/best-javascript-data-structures/

5. 빅오 소개

빅오는 수학과 연관이 깊은 개념이다!

• 빅오 표기법이 필요한 이유?
  알고리즘 해결법은 수십까지가 있는데 어떤 것이 최고인지 어떻게 판단할까?

"여러가지 코드를 일반적을 서로 비교하고 성능을 평가하는 방법"

문자열을 받아서 이것을 뒤집어서 출력하는 함수를 쓰는 과제에서도 10가지 정도의 해결방법이 있다.
For Loop, While loop 등등.. 이 중에 무엇이 더 좋은지 빅오라는 기준을 통해 판단 가능하다.

제대로 작동하기만 하면 되잖아? 라고 생각할 수 있으나,
기업 면접을 보거나, 코드 챌린지를 해결하거나, 큰 데이터셋을 다루는 대기업에서는 성능이 중요해지므로
시간 복잡도는 중요해진다.
또한 평소 현업에서도 비효율적인 코드를 찾고 디버깅하는데 중요할 것이다.

6. 코드 시간 재기

• 예시1: For Loop을 쓴 함수

function addUpTo(n) {
	let total = 0;

  	for (let i = 1; i <= n; i++) {
    	total += i;
    }
  
  	return total;
}

• 예시2: For Loop을 쓰지 않은 함수

function addUpTo(n) {
	return n * (n + 1) / 2; //수학공식.
}

더 나은 것의 정의

• 빠를 것 <= 가장 중요.
• 메모리를 덜 쓸 것
• 읽기 편할 것

timer함수를 쓰면 브라우저가 이 문서를 만든 시간, 즉 창이 열린 시간을 가르쳐 줌.

let t1 = performance.now();
addUpTo(1000000000);
let t2 = performance.now();
console.log(`Time Elapsed ${(t2 - t1) / 1000} seconds.`);

t1와 t2의 차를 빼면 함수의 실행전과 후 사이에 얼마나 소요되었는 지 확인이 가능.

결과적으로 예시2가 훨씬 시간이 덜 걸리는 것을 확인할 수 있다.

시간 측정에 관한 문제
1. 기계마다 결과가 다를 수 있다.
2. 기계가 같더라"도" 결과가 다를 수 있다.
3. 빠른 알고리즘의 경우 너무 빠른 나머지 측정 정확도가 떨어질 수 있다.

7. 연산 개수 세기

시간 측정이 아닌 다른 방법으로 어떻게 코드 성능을 판단할까?
컴퓨터가 처리해야하는 연산 갯수를 세면된다. 어떤 환경과 사양이든 그 개수는 변하지 않기 때문이다.

• 예시2: For Loop을 쓰지 않은 함수

function addUpTo(n) {
	return n * (n + 1) / 2; //곱셈, 덧셈, 나눗셈
}

위 예시2번을 보면 곱셈 한번, 덧셈 한번, 나눗셈 한번.
총 3번의 연산만 한다.

• 예시1: For Loop을 쓴 함수

function addUpTo(n) {
	let total = 0; //할당

  	for (let i = 1; i <= n; i++) { //할당, 비교, 덧셈
    	total += i; //덧셈, 할당
    }
  
  	return total;
}

위 예시1번을 보면, 여러가지 연산을 N의 크기만큼 반복한다.

즉 N이 커질수록 연산의 갯수도 비례적으로 늘어난다.

8. 시간 복잡도 시각화하기

👇 7가지의 함수의 N에 따른 시간 복잡도를 그래프로 보여주는 사이트.

https://rithmschool.github.io/function-timer-demo/

예시 1에 비해 예시 2가 압도적으로 성능이 좋음을 확인할 수 있다.

9. 빅오에 대한 공식 소개

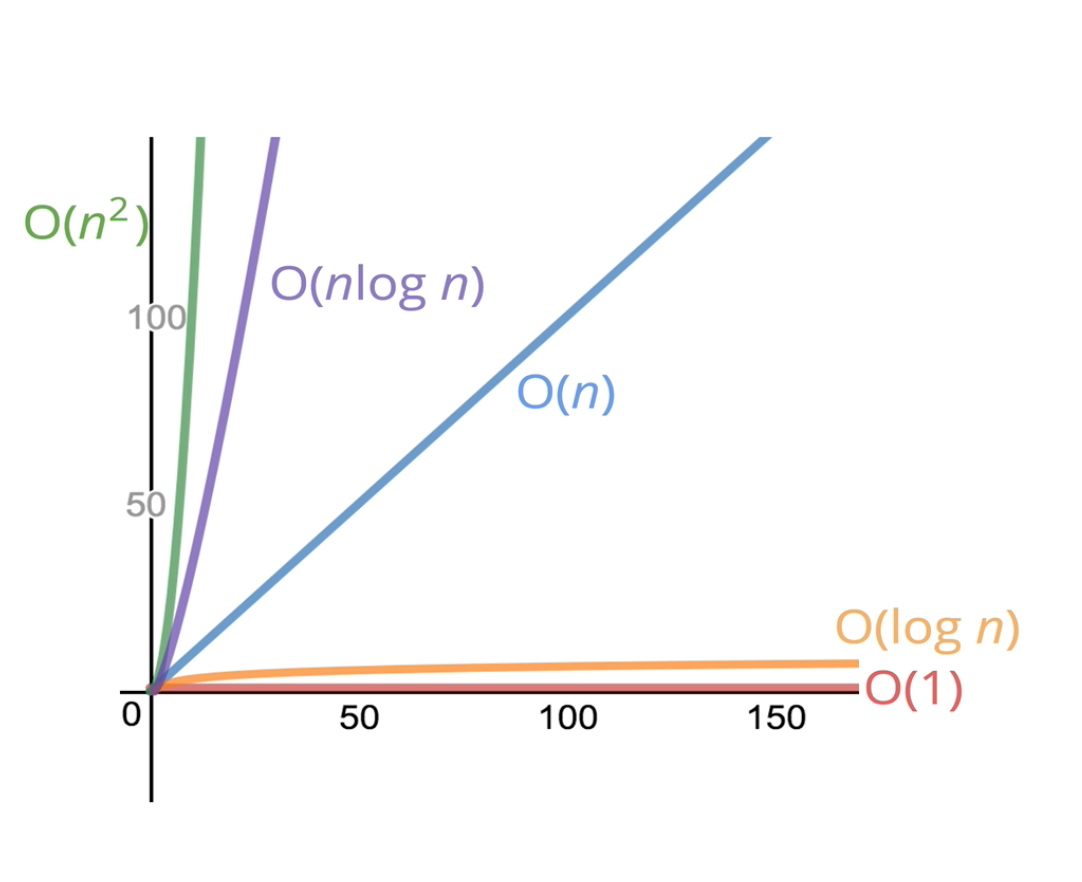
• Big O?
  정식으로 입력된 내용이 늘어날 수록 알고리즘에 실행 시간이 어떻게 변하는지 설명하는 공식적인 방식.
  오로지 전반적인 추세에 주목함.

방금 전, For Loop을 이용한 예시 1에서 N의 값이 늘어나는 것과 비례하여 1:1 비율로 선형으로 늘어난 추세가 있었다.
이것을 바로 빅오로 정의가능하다.

빅오는 실행시간이 갖을 수 있는 최대치.
일반적으로 가장 높은 실행시간들을 말한다.

예시 1 For Loop: O(n)
예시 2 수식: O(1)
예시 3 For Loop이 병렬적일 때: O(n)
예시 4 For Loop이 중첩일 때: O(n*2) O of N squared

10. 빅오 표현식의 단순화

O(2n) => O(n)
O(500) => O(1)
O(13n²) => O(n²)

O(n + 10) => O(n)
O(1000n + 50) => O(n)
O(n² + 5n + 8) => O(n²)

그래프를 아주 멀리, 우주에서부터 바라보고 추세(trend)를 분석하자고 생각하자.

• 첫번째, 산수는 상수이다.
  덧셈, 곱셈 등 2+2와 2백만 + 2를 처리하는 시간은 똑같다.

• 변수할당은 상수이다.
  x = 10과 x = 10만을 처리하는 시간은 똑같다.

• index나 key를 이용해서 배열이나 객체에 접근하는 것은 상수이다.
  array[0]과 array[100000]을 처리하는 시간은 똑같다.

• 루프가 있으면 복잡도가 루프의 길이 루프안에 있는 연산들이 된다.
  N 루프내부의 작업양

function logAtLeast5(n) {
	for (let i = 1; i <= Math.max(5, n); i++) {
    	console.log(i);
    }
}

위 함수는 5이하의 숫자가 들어오면 5까지 숫자를 콘솔로그하고
5초과의 숫자가 들어오면 그 숫자까지 콘솔로그한다.
이 함수의 빅오는?

O(n)

라고 단순화해서 말할 수 있다.

function logAtMost5(n) {
	for (let i = 1; i <= Math.min(5, n); i++) {
    	console.log(i);
    }
}

위 함수는 5이하의 숫자가 들어오면 그 숫자까지 콘솔로그하고
5초과의 숫자가 들어오면 5까지만 콘솔로그한다.
이 함수의 빅오는?

O(1)

라고 단순화해서 말할 수 있다.

11. 공간 복잡도

입력 되는 것을 제외하고 알고리즘 자체가 필요로 하는 공간을 의미.
사실상 "보조 공간 복잡도"를 뜻함.

불린, 숫자, undefined, null은 자바스크립트에서 모두 불변 공간.
그러나 문자열, 참조 reference 타입, 배열과 객체는 O(n) 공간이 필요.

function sum(arr) {
	let total = 0; // 상수 공간

    for (let i = 0; i < arr.length; i++) { // 상수 공간
      total += arr[i]
    }

	return total; //숫자가 커진다고해서 차지하는 공간이 커지진 않음.
}

입력의 크기가 차지하는 공간과 숫자의 크기는 상관이 없다.
차지하는 공간은 위 두 변수 뿐. 새 변수를 생성하거나 하지는 않음.
이를 O(1) 공간이라고 한다.

function double(arr) {
	let newArr = []; // 입력값에 따라 저장되는 값의 개수가 바뀜.

    for (let i = 0; i < arr.length; i++) { // 상수 공간
      newArr.push(2 * arr[i]);
    }

	return newArr; //n numbers
}

위는 O(n)공간의 예시. 입력값에 따라서 return하는 배열의 크기가 달라짐.

function subtotals(array) {
    var subtotalArray = Array(array.length);
    for (var i = 0; i < array.length; i++) {
        var subtotal = 0;
        for (var j = 0; j <= i; j++) {
            subtotal += array[j];
        }
        subtotalArray[i] = subtotal;
    }
    return subtotalArray;
}

위 역시 O(n)공간의 예시.

12. 로그와 섹션 요약

로그 개념은 수학과 연관이 매우 깊음.
로그함수는 지수함수의 역함이다.
또한 나눗셈과 곱셈이 짝인것처럼 로그함수와 지수함수는 짝이다.

switching around!

log₂(8) = 3 => 2³ = 8
log₂(value) = exponent => 2exponent = value

빅오에서는 전반적인 추세만 중요히 보기 때문에 log³ log₅ 등등을 모두 log라고 표기.

log === log₂

어떤 이진 로그를 대략 계산하기 위해서는 그 숫자가 1보다 작아지기 전에 2로 나눠지는 횟수

8 /2
4 /2
2 /2
1

위 예시는 3

25 /2
12.5 /2
6.25 /2
3.125 /2
1.5625 /2
0.78125

위 예시는 약 4.64

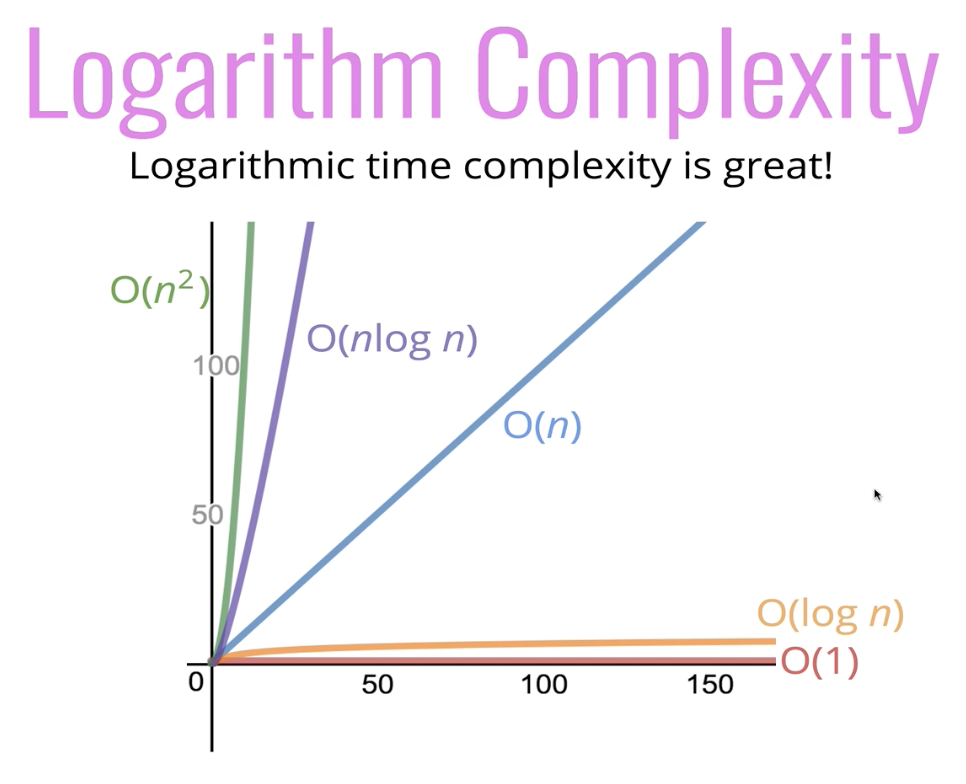
그리고 O(log n)은 O(n)보다 훨씬 낫다!

로그 개념은 어디서 찾을 수 있을까?
1. 몇 탐색 알고리즘
2. 효율적인 정렬 알고리즘
3. 재귀함수는 가끔 로그 복잡도일 때가 있다.

Recap

• 알고리즘의 성능을 평가하기 위해서 우리는 빅오 표기법을 사용한다.
• 빅오를 통해서 시간복잡도와 공간복잡도의 깊은 이해가 가능하다.
• 빅오의 분석에 있어서 정확성보다는 전반적인 추세가 중요하다. (우주에서 바라봤을 때 모습)
• 빅오로 측정되는 알고리즘의 시간 및 공간복잡도는 하드웨어의 영향을 받지 않는다.