동적 프로그래밍

유키미아우·2023년 10월 18일

본 포스팅은 Colt Steele의 JavaScript 알고리즘 & 자료구조 마스터클래스를 수강하며 정리한 노트입니다.
https://www.udemy.com/course/best-javascript-data-structures/

동적 프로그래밍 소개

문제를 푸는데 사용할 수 있는 접근법 중 하나.
복잡한 문제를 더 간단한 하위 문제의 모음으로 쪼갠 후,
각 하위 문제가 반환하는 값을 중간저장하는 방식으로 문제를 해결한다.

✅ 동적 프로그래밍을 적용 가능하다는 시그널:
1. 하위 문제가 있는가?
2. 최적 부분구조를 가지고 있는가?

재귀함수와 익숙하다면 동적 프로그래밍을 이해하는데 더 도움이 될 것이다!

이름의 유래?

동적 프로그래밍이라는 이름은 오해를 불러 일으키기 쉽다.
마치, 여러가지 일을 하거나...(?) 활발히 변화하는 값을 다루거나...(?) 아주 빠르게 움직이는듯한(?) 어감으로 들리지만 이름의 유래는 컴퓨터 공학과는 관련이 없었다.

동적 프로그래밍은 1940년대 Richard Bellman이 고안하였고, 원래는 군대의 일정을 최적화하는 것을 가르키는 단어였다.

수학에 대한 병적 혐오를 가진 상사로부터 연구활동 내부의 수학적 측면을 지적받지 않기 위해서 어떻게든 덜 수학적인 용어를 채택해야만 했다고... 본인 인터뷰
"동적 프로그래밍은 확실히 다이내믹하고 다층적이며 시간에 따른 변동성이 있으므로, 이 네이밍을 통해서 두마리 토끼를 한번에 잡고싶었다."

위와 같은 유래에 관한 이야기는 차치하고, 동적 프로그래밍을 가장 심플하게 표현할 수 있는 문장은 "최적의 해답을 찾아내는 것"이다!

동적 프로그래밍은 다음과 같은 특정 상황에서만 제대로 작동한다.

첫째로, 반복되는 하위 문제가 있다!

한 문제를 더 작은 문제들로 나눌 수 있고, 그 조각들 중 일부가 재활용 가능할 때. 각각의 조각이 다른 모습이면 안되고 재사용성이 있어야한다.

대표적으로 피보나치 수열은 반복되는 하위 문제들을 가지고 있어 여기에 해당된다.

f(n) = f(n - 1) + f(n - 2)

같은 공식이 중간값 저장을 하며 똑같은 동작을 계속 반복한다.

1, 1, 2, 3, 5, 8, 13, 21, 34 .........

그러나 합병 정렬(merge sort)의 경우 하위문제가 반복되지 않으므로 해당되지 않는다. 머지소트하는 대상체가 그때그때 달라지기 때문. 따라서 합병정렬의 풀이는 분할 정복(devide concuer)에 해당한다.

mergeSort([10, 24, 10, 24]);과 같은 매우 예외적 케이스가 아닌 이상 동적 프로그래밍을 적용할 수 없다...

정리:

분할 정복(Divide and Conquer): 하위 문제에 동일하게 중복이 일어나지 않을 때 적용.
동적 프로그래밍(Dynamic Programming): 하위 문제에 동일하게 중복이 일어날 때 적용.

둘째로, 최적 부분구조를 가지고 있다!

하위 문제의 최적 해답을 통해서 전체문제의 최적 해답을 구할 수 있는 구조

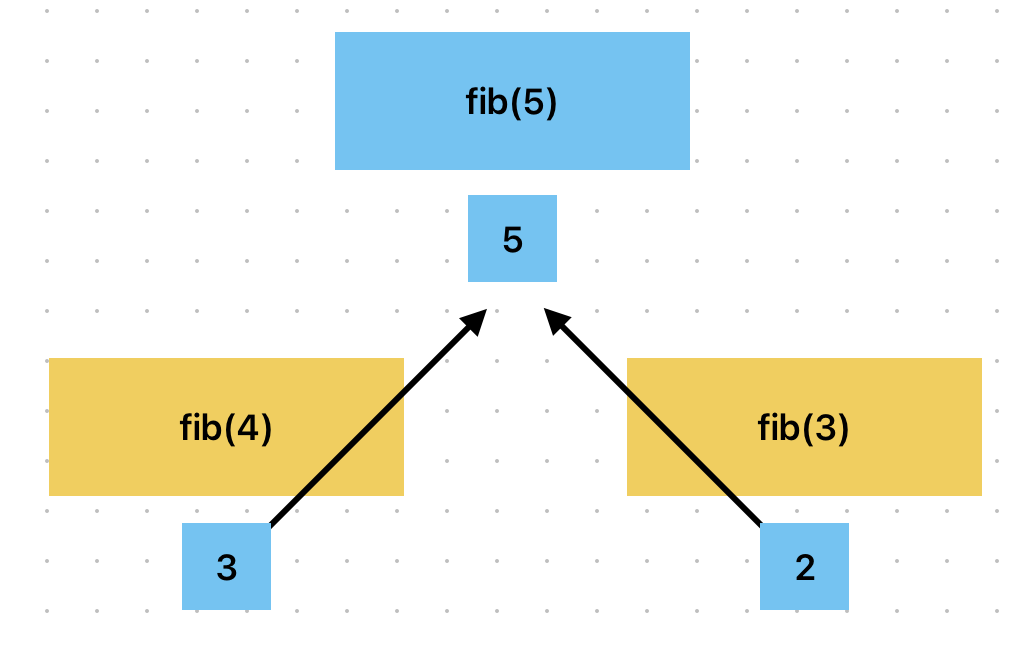
피보나치 수열 예시
5번째 피보나치 수를 찾으려면 최적의 해답은 세번째와 네번째에 있다는 것.

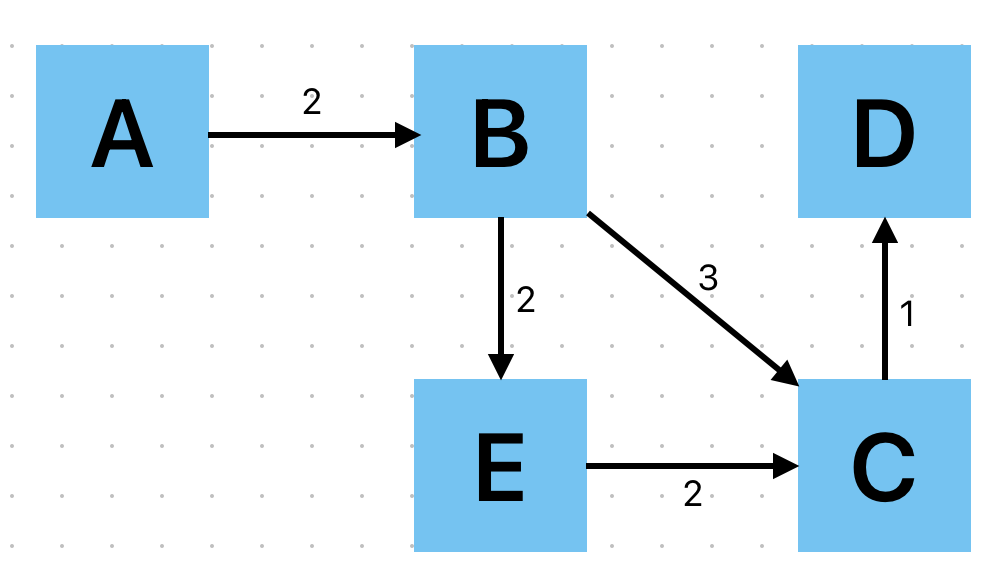
최단거리 예시
시작지점에서 끝지점으로 가는 최단 경로에 대해서 다루는 경우 그 경로가 무엇인든간에 해당 경로 위에 있는 한 지점에 대해서는 그 경로가 최단 거리가 된다.

따라서 A, B, C, D로 가는 경로는 C로 가는 최단 경로와 B로 가는 최단 경로를 포함한다.

동적 프로그래밍이 없는 단순 재귀적 솔루션 작성

피보나치 수열을 동적 프로그래밍을 사용하지 않고 풀어보자.

	function fib(n) {
    	if (n <= 2) return 1;
      	return fib(n - 1) + fib (n - 2);
    }

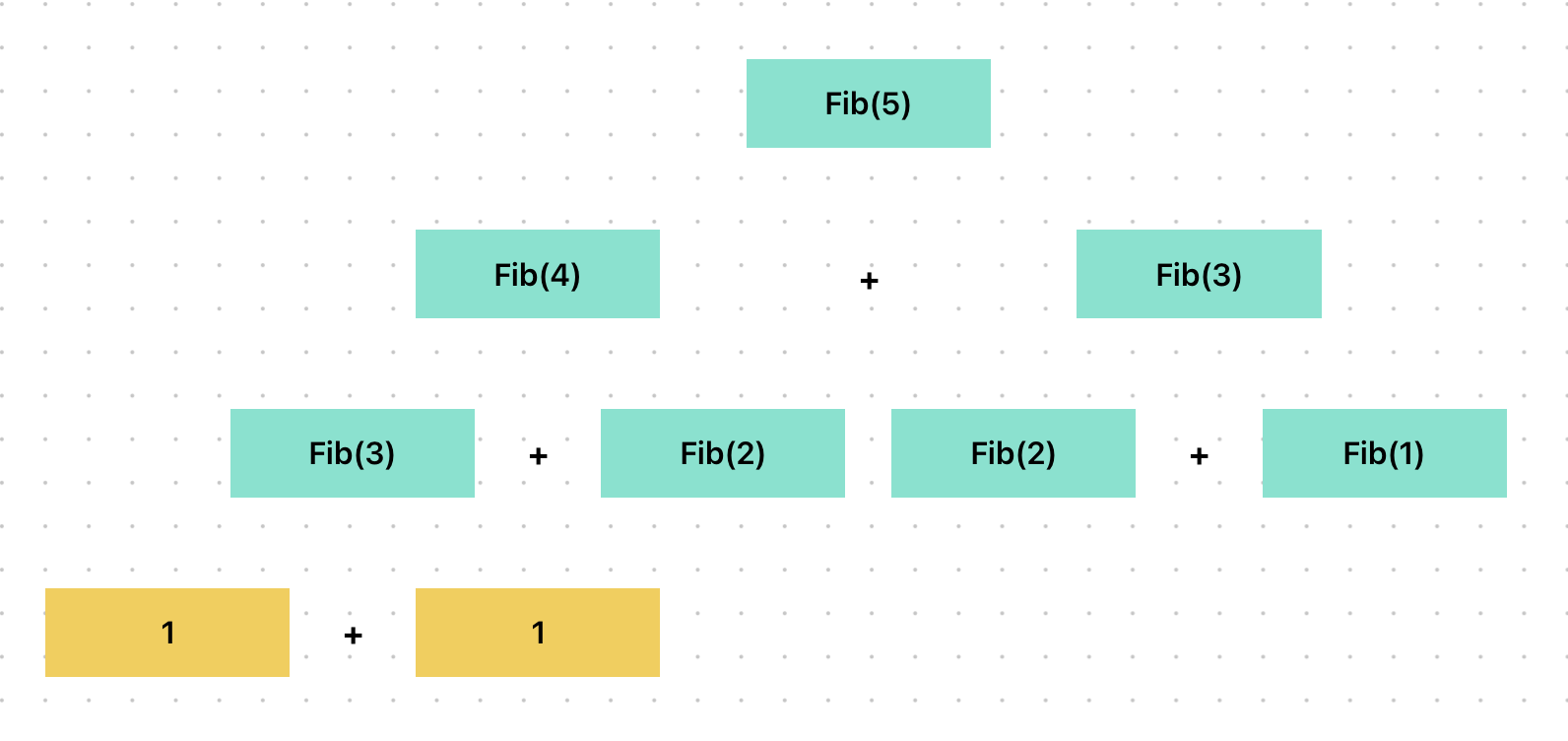
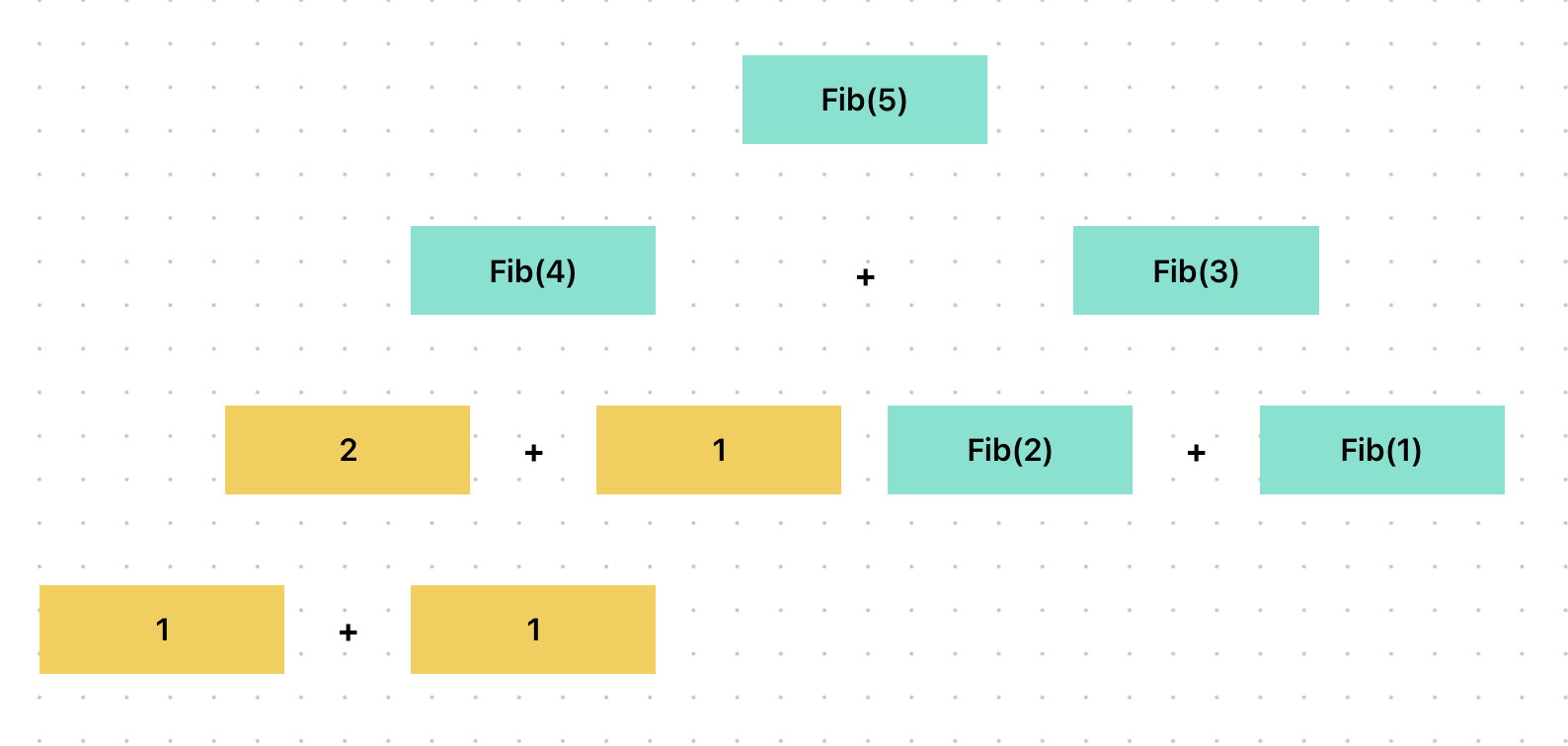
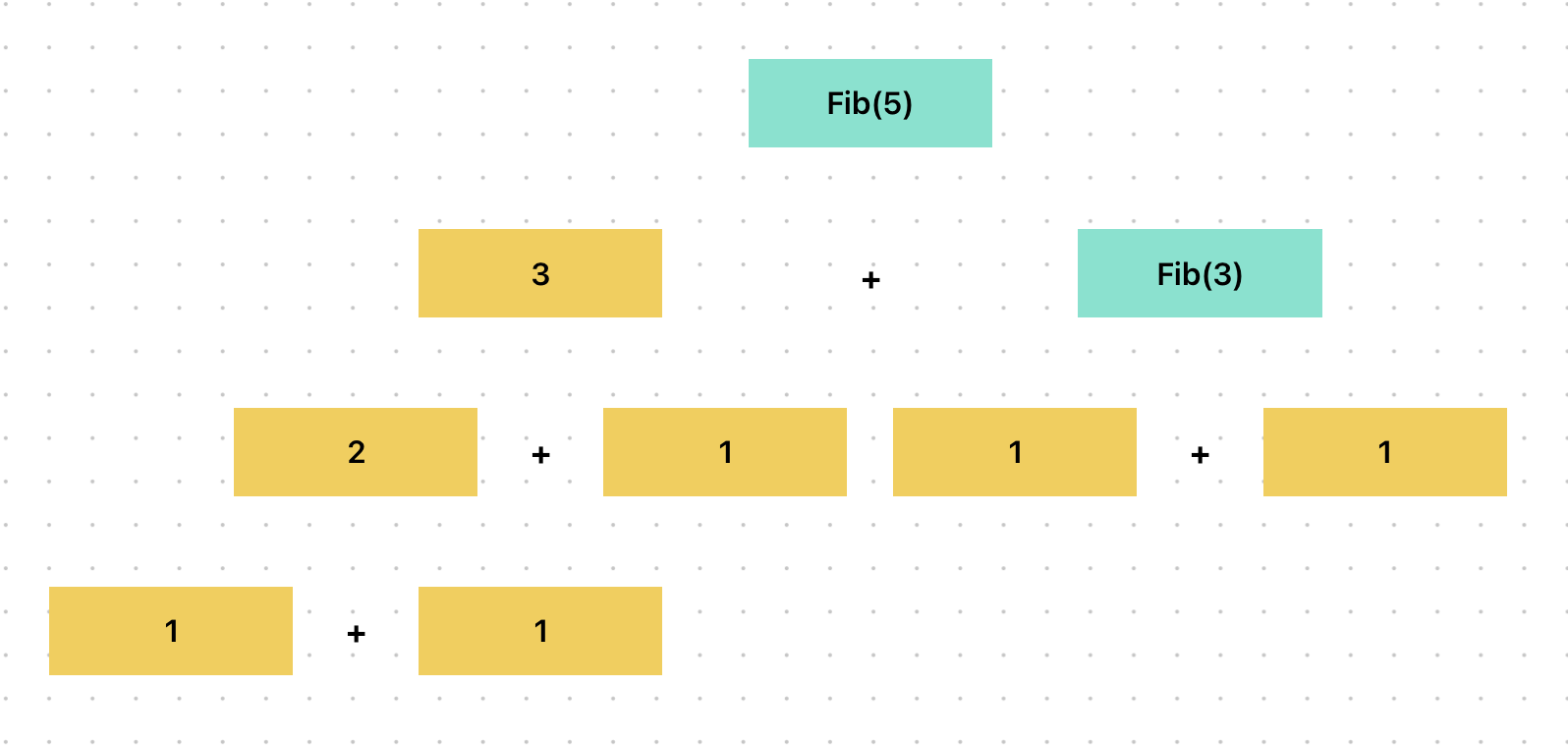
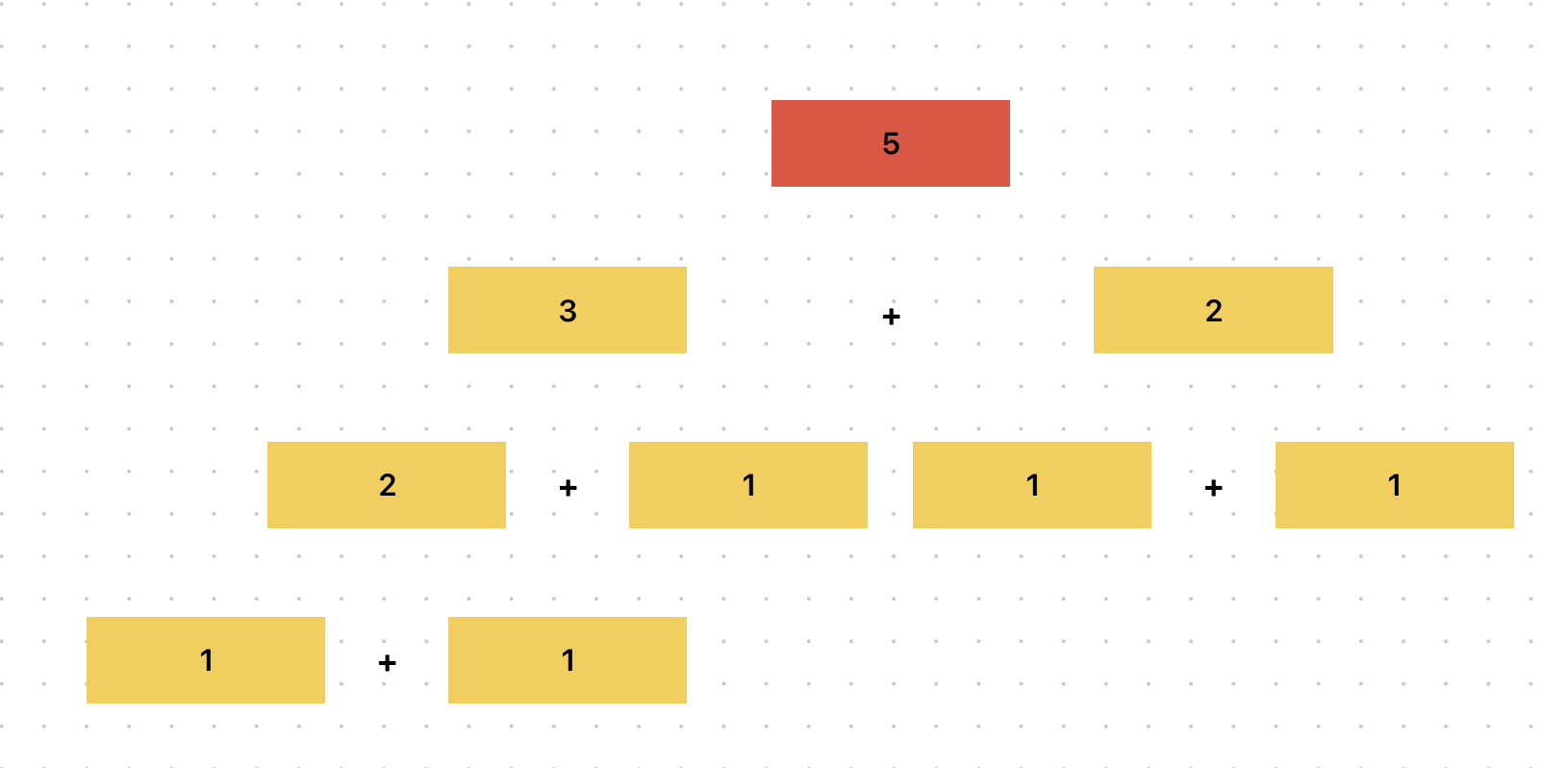
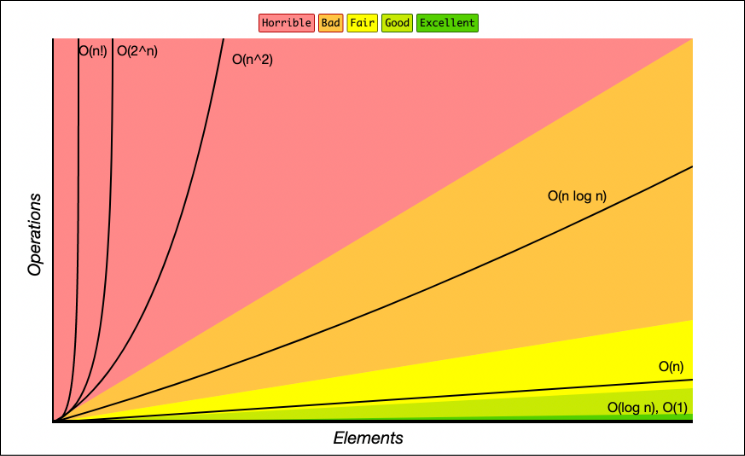
위 재귀함수는 짧고 간결하기는 하나 O(2^n)로 시간복잡도가 매우매우 낮아 비효율적이다.
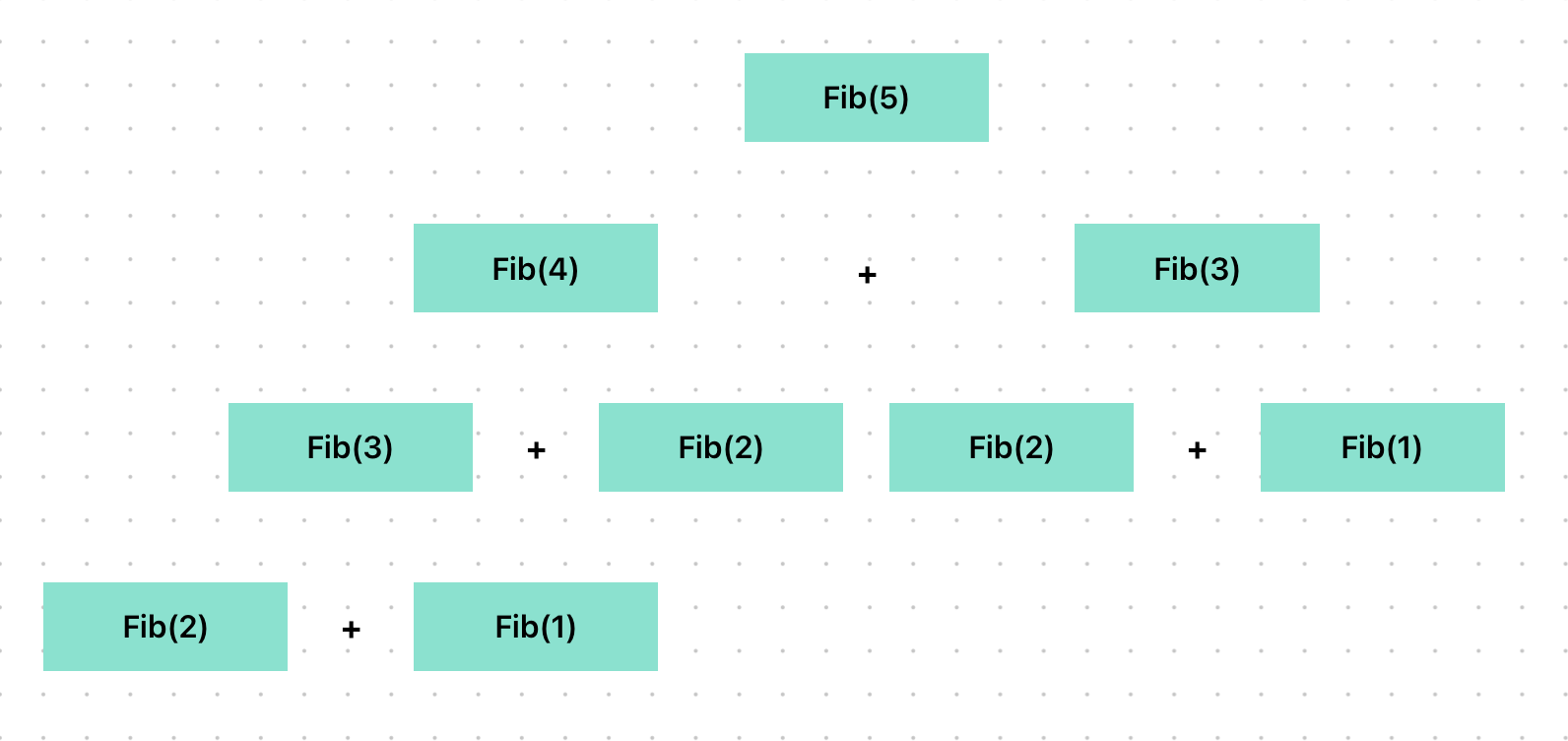
n의 숫자가 크면 클 수록 트리의 스케일이 우후죽순 커진다!
fib(45)를 넣기만 해도 10초정도 소요되므로 fib(100)은 실험하지 않는게 정신건강에 좋다..

또한 연산의 결과를 저장해두지 않기 때문에 같은 연산을 수없이 반복하는 문제가 발생하고 있다.

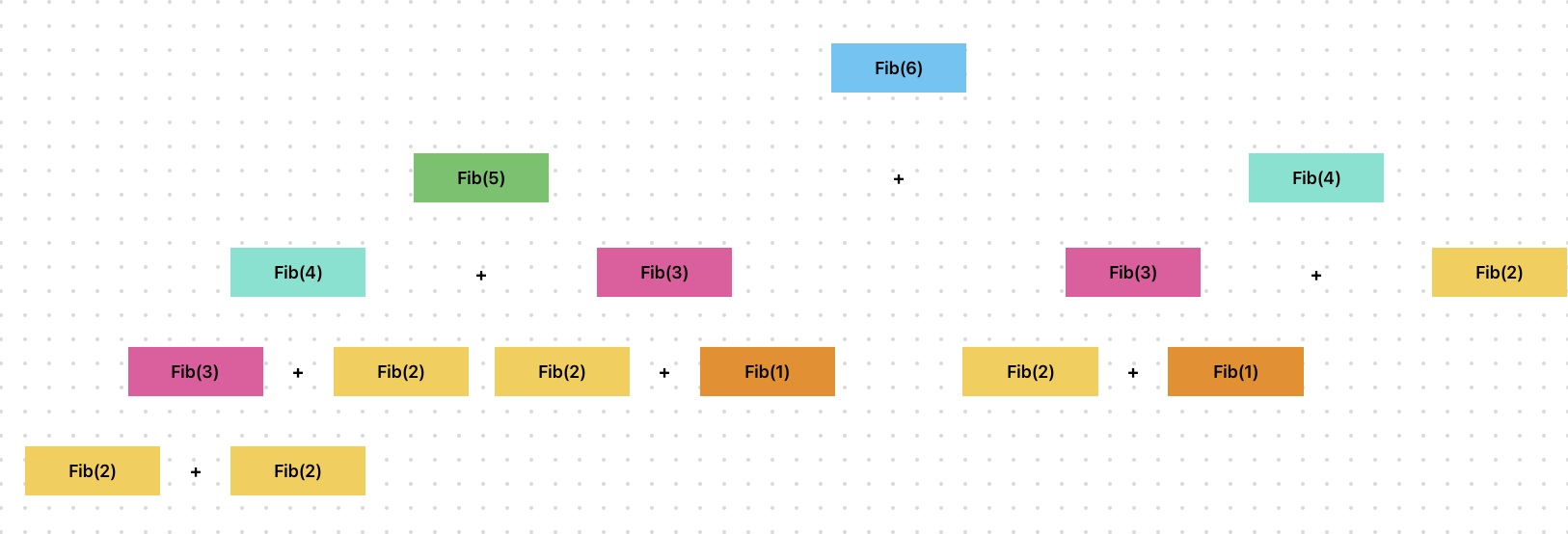
중복되는 하위문제를 색상으로 칠해보았다.
한번 연산을 한 내용인데 또 반복할 때의 비용이 너무 아깝지 않은가?

그러므로 중간 계산의 결과 값을 저장해 놓아 효율을 끌어올리는 것이 동적 프로그래밍의 핵심이다.

Memoization & 재귀, 바텀-탑 방식

메모이제이션은 같은 인풋이 주어졌을 때에 미리 캐시된 결과 값을 반환해줌으로써 복잡한 함수의 작동비용을 줄여준다.

f(5) 를 했을 때 결과를 저장해두고
나중에 f(5)가 다시 콜되면 캐시된 결과값을 활용한다.

	function fib(n, memo=[]) {
    	if (memo[n] !== undefined)  return memo[n]; // n번째 인덱스에 값이 있나? 체크
      	if (n <= 2) return 1; // 베이스케이스 (기반 조건)
    
      	let res = fib(n - 1, memo) + fib(n - 2, memo);
      	memo[n] = res; // 메모
      
      	return res;
    }

f(5)의 결과 값은 메모의 5번째 인덱스에 저장하고 접근.
f(10)의 결과 값은 메모의 10번째 인덱스에 저장하고 접근.

fib(100)을 실행시켜도 1초가 걸리지 않는 모습!

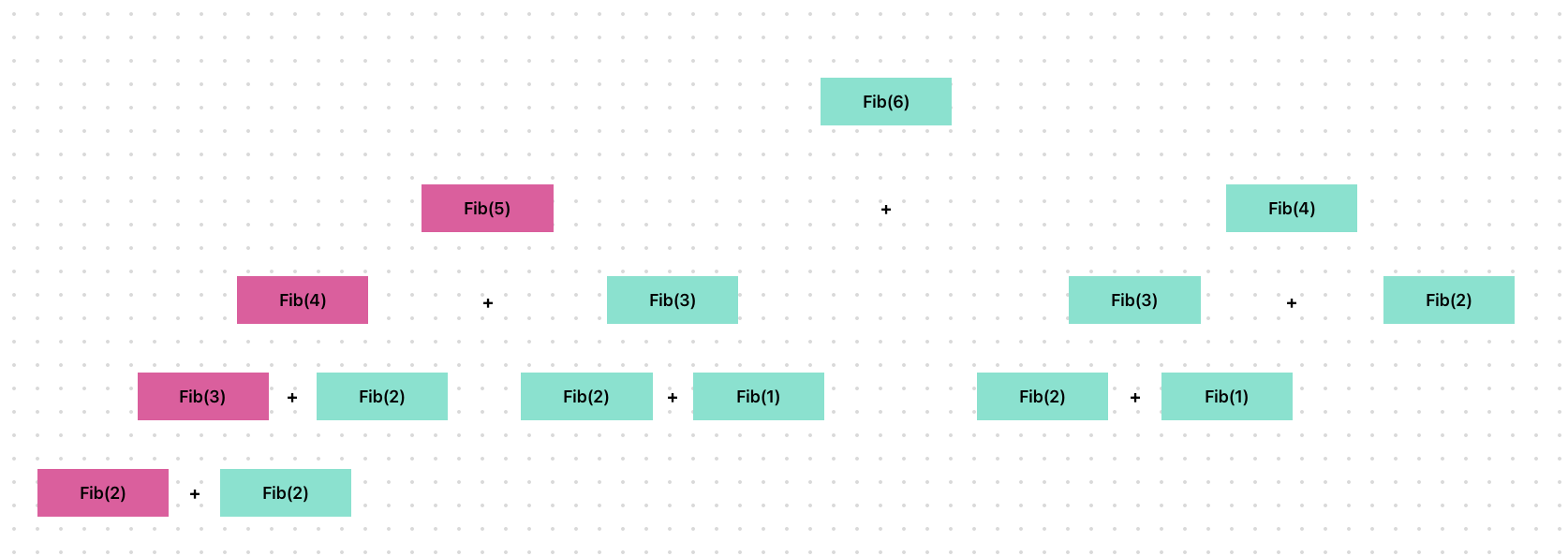
분홍색 함수실행해서 처음으로 값이 도출된 후부터는 새롭게 연산을 하지 않는것을 색상으로 표현한 모습.

아래와 같이 기반케이스를 배열에 미리 할당해버린다면 더 간결하게 작성 가능

	function fib(n, memo=[undefined, 1, 1]) { // n이 2보다 작은 경우 결과값을 처음부터 배열에 넣고 출발
    	if (memo[n] !== undefined)  return memo[n];
      	let res = fib(n - 1, memo) + fib(n - 2, memo);
      	memo[n] = res; // 메모
      
      	return res;
    }

처음으로 값을 구하는 연산의 실행 수는 n의 크기에 비례한다.
또한 메모배열에서 값에 접근하는 것은 상수시간이 걸린다. O(1)

O(n) + o(1)이므로 전체적 트렌드는 O(n)이 되며 O(n^2)에 비해 어마어마한 개선이 이루어진 것을 알 수 있다!

출처

for문 & 타뷸레이션, 탑-바텀 방식

같은 문제를 상향식으로 접근한다면 어떨까?

	function fib(n) {
      	if (n <= 2) return 1;

      	let fibNums = [undefined, 1, 1]; // 값을 저장할 테이블. 베이스케이스는 미리 저장한 모습.
    	
      	for (let i = 3; i <= n; i++) { // 1, 2는 각각 1, 1임을 알고 있으므로 3부터 출발.
        	fibNums[i] = fibNums[i - 1] + fibNums[i - 2];
        }
      
      	return fibNums[n]; // n번까지 루프 후 값을 반환하며 종료
    }