
보자마자 쉽네! 라고 생각했는데
과정이....짧지가 않았다.
그래서 코드가
졸라.....길다
아래가 내 코드
function solution(n, m) { var answer = []; let nnumber = [] let mnumber = [] for (i=0; i<=n; i++){ if(n%i===0){ nnumber.push(i) } } for (i=0; i<=m; i++){ if(m%i===0){ mnumber.push(i) } } answer.push(nnumber.filter(a=> mnumber.includes(a)).sort((a,b)=> a-b).pop()) for(let j = 1; j <=n*m; j++){ if(j % n ===0 && j % m === 0){ answer.push(j) break; } } return answer; }
까여도 할말이 없다
진짜로 ㅋㅋ
과정이 어떻게 되냐면
1. n의 모든 약수를 전부 nnumber의 배열에 담는다
2. m의 모든 약수를 mnumber의 배열에 담는다
3. 그 둘을 비교를 해서 중복되는 값이 있을 경우 오름차순 정렬을 해서 제일 오른쪽(제일 큰 수)를 제출할 answer에 담아준다. (최대공약수)
4. 반복문을 돌아서 n*m의 수까지 빙글빙글 돌면서 나눠주는 값을 j값을 1씩 올려준다.
5. j값을 1씩 올리면서 n을 나눠서 나머지가 0이 나올 때, m을 나눠서 나머지가 0이 나올 경우
6. 그 값을 answer에 담아주고, 반복문을 멈춘다. (최소공배수)
지이이이이이이이이이이인자 비효율적이다
최소공배수는 괜찮다. 짧으니까!!
근데 공약수를 구하는 과정이 복잡하다, 두개의 반복문을 돌려야하니까....
그래서 조금 더 스마트하게 값을 구할 순 없을지 서칭을 하다가 처음 보는 법칙(?)을 찾았다.
바로 유클리드 호제법이라는 것인데, 이해는 했지만 그... 설명하는건 좀 어려울 것 같아서 서술을 같이 하면서 풀어보겠다.
참고한 링크!
JavaScript로 최대공약수(GCD), 최소공배수(LCM) 구하기
위키백과 유클리드 호제법

우와와와...................
결국은 A % B = C라면 B % C = D
C % D = 0 라면 D가 최대공약수가 된다는 소리다.
하지만 A가 B보다 작을 경우에 문제가 되는데 그러한 부분을 함수의 형태로 위에 걸어놓은 블로그에 설명을 해주시고 있다.
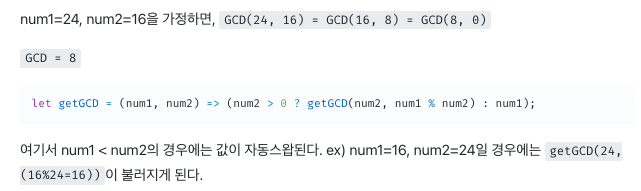
이 사진을 보면 재귀함수로 만들어놨는데
예를 들어서 값이 134 , 515 라고 한다면 이런 순서로 돌아간다
134, 515 -> 515, 134 -> 134, 515 % 134 -> 113 , 134 % 111 ->
23 , 111 % 23 -> 19 , 23 % 19 = 4, 19 % 4 -> 3 , 4 % 3 -> 1, 3%1
2, 2%1 -> 1, 1%1
num2 = 0 이 되므로 num1에 있는 1이 최소공약수가 된다.
그렇기에 최소공약수는
const gcd = (a, b) => a % b === 0 ? b : gcd(b, a % b); gcd(사용해야하는 값 1, 사용해야하는 값2)의 방식으로 사용할 수 있다.
최대공배수도 방법이 적혀있는데 내가 바보멍청이 인건지 카페인이 모자른지 계산이 머리속에서 회전이 안돼.....
나중에 이해가 되면 추가해보겠다
