🌟 선형 회귀 Linear Regression
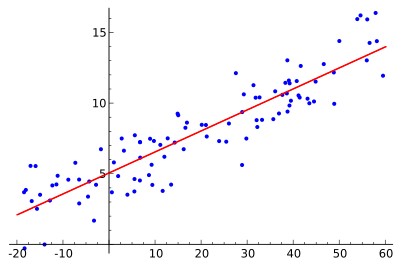
지도 학습의 예시 Example of Supervised Learning
예시에 "적합한 답"을 줌
실제 자료인지 수치 데이터 제공 = 회귀 문제의 예시
선형 회귀(Linear Regression) 모델과 평균 제곱 오차(Mean Squared Error, MSE)는 다음과 같이 파이썬 코드로 작성 가능
import numpy as np
class LinearRegression:
def __init__(self):
self.weights = None
def fit(self, X, y):
# Add a column of ones for the bias term
X = np.hstack((np.ones((X.shape[0], 1)), X))
# Calculate the optimal weights using the normal equation
self.weights = np.linalg.inv(X.T @ X) @ X.T @ y
def predict(self, X):
# Add a column of ones for the bias term
X = np.hstack((np.ones((X.shape[0], 1)), X))
# Make predictions using the learned weights
y_pred = X @ self.weights
return y_pred
def mean_squared_error(y_true, y_pred):
return np.mean((y_true - y_pred)**2)선형 회귀 모델은 클래스로 구현
fit 메소드를 사용하여 데이터를 학습하고,
predict 메소드를 사용하여 새로운 데이터에 대한 예측을 수행
평균 제곱 오차는 단순히 두 배열의 차이의 제곱의 평균을 계산하는 함수로 구현
주택 가격 예측 예시
m = 학습 예제의 수, 47개의 학습 예제
x = feature
y = 목표 변수
(x, y) = one training example
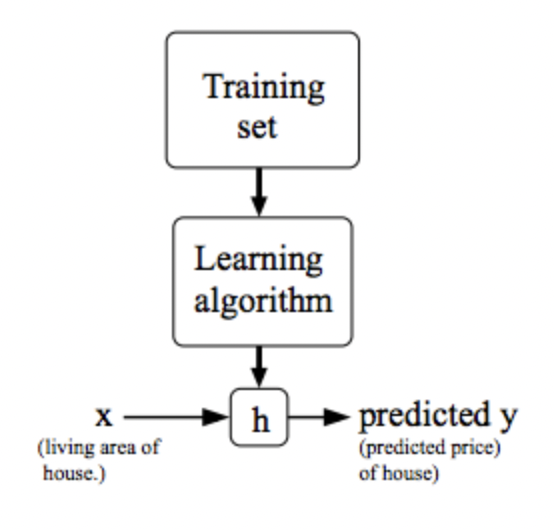
Training Set
-> Learning Algorithm
-> h(가설)
x -> h ->
h를 표현하기 위해서 🤚
h(x) = 세타0 + 세타1x
선형 함수인 y를 예측하는 것
선형 함수를 사용하는 이유 🤷♂️
선형 유형은 간단한 빌딩블록
선형 회귀의 값은 하나이며, 이 값은 x
하나의 x 값으로 모든 가격을 예측함
비용 함수 수학적 정의 🎢
Cost = 오차요인 제곱 함수 (h(x) - y)^2 가장 최소화 하려면
(1/2m)i=1Σm(h(x) - y)^2
i = 1부터 m까지 비용의 총합의 제곱의 평균
(h(x(i)) - y(i))^2
결국 Cost를 최소화 하는 것은 세타0, 세타x(i)에 달려있음
비용 함수 하는 일, 사용하는 이유 🤷♂️
Parameters에 따라 다른 직선으로 표현됨
최적화된 목표 = Cost의 최솟값
가설 함수와 비용 함수를 이해해야 함
Hypothesis - 가설
Parameters - 파라미터
Cost Function - 비용 함수
Goal - 최적의 목표
기울기 하강
거의 모든 회귀에서 사용하는 알고리즘
초기값을 확인 : Cost를 줄이기 위하여
높은 언덕에서 가장 빨리 내려가려고 하는 방법
a := a+1
==
a = a+1;
a = b
==
a == b ? True : False;당신의 시간이 헛되지 않는 글이 되겠습니다.
I'll write something that won't waste your time.
