플로이드 워셜 알고리즘 (Floyd-Warshall)

플로이드 워셜 알고리즘 (Floyd-Warshall)

그래프의 모든 최단 경로를 구하는 알고리즘

• 모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구한다.
• 시간 복잡도 O(n^3)
• 공간 복잡도 O(n^2)
• 음의 가중치를 갖는 간선이 있어도 되지만, 합이 음수 가중치를 갖는 사이클이 있으면 안된다.
• DP(동적계획법)을 활용한 방법이다.

알고리즘 구현

(노드 i ~ 노드 j)의 최단 거리 :
graph[i][j] = Math.min(graph[i][j], graph[i][k]+graph[k][j]);
-> 경유할 수 있는 새로운 노드 k를 선택하고, 더 짧은 길이를 선택하여 줄이는 과정을 반복한다.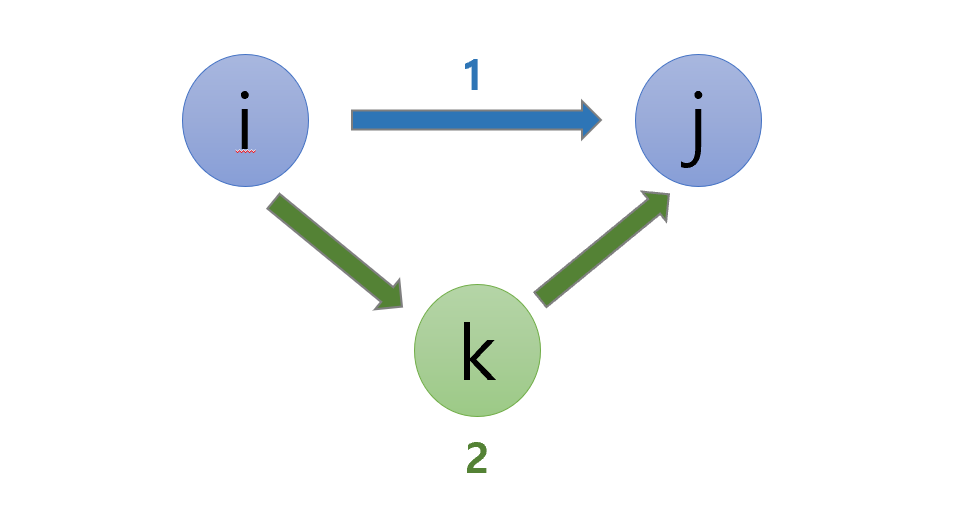 

// graph : 2차원 인접 행렬, n = 노드의 개수
	public static void floyd(int[][] graph, int n) {
		for (int k = 1; k <= n; k++) {
			for (int i = 1; i <= n; i++) {
				for (int j = 1; j <= n; j++) {
					graph[i][j] = Math.min(graph[i][j], graph[i][k]+graph[k][j]);
				}
			}
		}
	}

그래프 최단 거리 구하는 알고리즘

1. 다익스트라 :
   한 점에서 다른 모든 점까지의 최단 거리를 구함 (음의 가중치를 허용X, 방문하지 않은 이웃 노드 중에서 최단 거리가 가장 가까운 노드만 방문)
2. 벨만 포드
   다익스트라 한계 극복 (음의 가중치를 허용O, 매단계마다 모든 간선을 전부 확인)
3. 플로이드-워셜 :
   모든 점에서 다른 모든 점까지의 최단 거리를 구함 (음의 가중치를 허용O, 경유하는 중간 노드 기준)