📖 LinkedList 2
📌 연결 리스트
✅ 리스트를 이용한 스택
-
리스트를 이용해 스택을 구현할 수 있다.
-
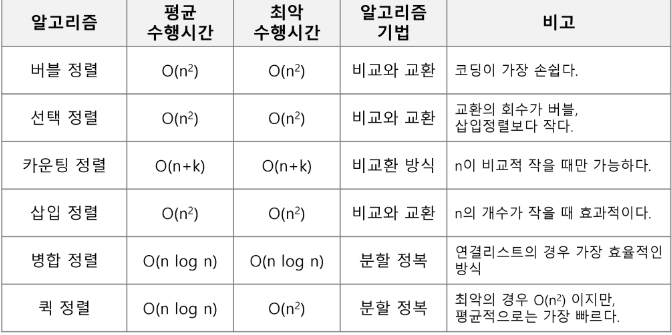
스택의 원소 : 리스트의 노드
- 스택 내 순서는 리스트의 링크를 통해 연결됨
- Push : 리스트의 마지막 노드 삽입
- Pop : 리스트의 마지막 노드 반환 / 삭제
-
변수 top
-
리스트의 마지막 노드를 가리키는 변수
-
초기 상태 : top = null
-
✅ 리스트를 이용한 Push와 Pop 연산 구현
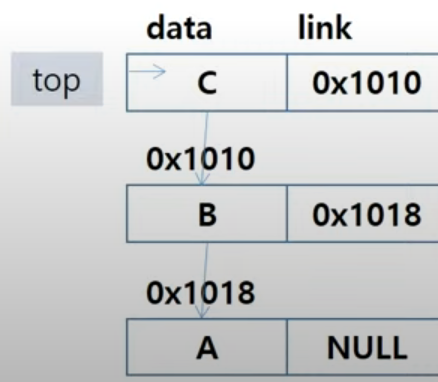
- null 값을 가지는 노드를 만들어 스택 초기화

- 원소 A 삽입 : push(A)

- 원소 B 삽입 : push(B)
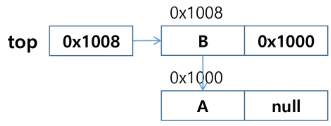
- 원소 C 삽입 : Push(C)
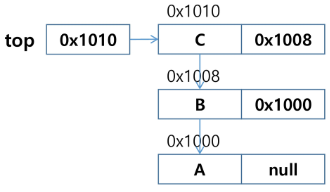
- 원소 반환 : Pop
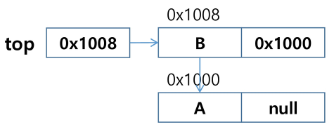
// AddToStart와 같다
push(i) { // 원소 i를 스택에 push
temp = createNode();
temp.data = i;
temp.link = top;
top = temp;
}pop() { // deleteStart와 같다
temp = top
if(top == null)
return 0;
else {
item = temp.data;
top = temp.link // top이 가리키는 노드 변경
free(temp);
return item;
}
}📌 연결 큐 (Linked Queue)
✅ 연결 큐의 구조
- 단순 연결 리스트(Linked List)를 이용한 큐
- 큐의 원소 : 단순 연결 리스트의 노드
- 큐의 원소 순서 : 노드의 연결 순서. 링크로 연결되어 있다
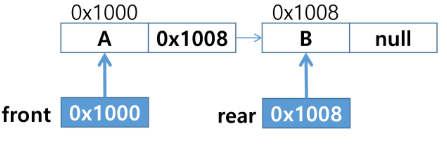
- front : 첫 노드를 가리키는 링크
- rear : 마지막 노드를 가리키는 링크
- 상태 표현
- 초기 상태 : front = rear = null
- 공백 상태 : front = rear = null

✅ 연결 큐의 연산 과정
- 공백 큐 생성 : createLinkedQueue()

- 원소 A 삽입 : enQueue(A)

- 원소 B 삽입 : enQueue(B)
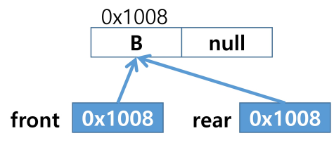
- 원소 삭제 : deQueue()
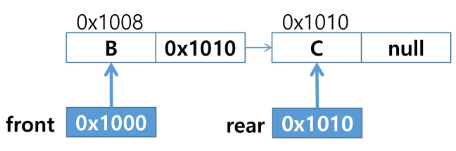
- 원소 C 삽입 : enQueue(C)
- 원소 삭제 : deQueue()
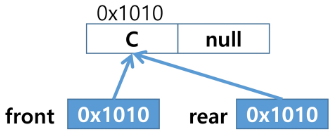
- 원소 삭제 : deQueue()

✅ 연결 큐의 구현
- 초기 공백 큐 생성 : createLinkedQueue()
- 리스트 노드 없이 포인터 변수만 생성함
- front와 rear를 null로 초기화
createLinkedQueue() {
front <- null;
rear <- null;
}- 공백 상태 검사 : isEmpty()
- 공백상태 : front = rear = null
isEmpty() {
if(front == null)
return true;
else
return false;
}- 삽입 : enQueue(item)
- 새로운 노드 생성 후 데이터 필드에 item 저장
- 연결 큐가 공백인 경우, 아닌 경우에 따라 front, rear 변수 지정
enQueue(item) {
new <- getNode(); // getNode() : 새 노드 할당 후 리턴
new.data <- item;
new.link <- null;
if(front == null) {
rear <- new;
front <- new;
} else {
rear.link <- new;
rear <- new;
}
}- 삭제 : deQueue()
- old가 지울 노드를 가리키게 하고, front 재설정
- 삭제 후 공백 큐가 되는 경우, rear도 null 설정
- old가 가리키는 노드 삭제하고 메모리 반환
deQueue() {
if(isempty())
Queue_Empty();
else {
old <- front;
item <- front.data;
front <- front.link;
if(isEmpty())
rear <- NULL;
free(old);
return item;
}
}✅ 우선순위 큐의 구현
-
배열을 이용한 우선순위 큐
-
리스트를 이용한 우선순위 큐
✅ 우선순위 큐의 기본 연산
-
삽입 : enQueue
-
삭제 : deQueue
✅ 배열을 이용한 우선순위 큐
-
배열을 이용하여 우선순위 큐 구현
- 배열을 이용하여 자료 저장
- 원소를 삽입하는 과정에서 우선순위를 비교하여 적절한 위치에 삽입하는 구조
- 가장 앞에 최고 우선순위의 원소가 위치하게 됨
-
문제점
- 배열을 사용하므로, 삽입이나 삭제 연산이 일어날 때 원소의 재배치가 발생함
- 이에 소요되는 시간이나 메모리 낭비가 큼
✅ 리스트를 이용한 우선순위 큐
- 리스트를 이용하여 우선순위
- 연결 리스트를 이용하여 자료 저장
- 원소를 삽입하는 과정에서 리스트 내 노드의 원소들과 비교하여 적절한 위치에 노드를 삽입하는 구조
- 리스트의 가장 앞족에 최고 우선순위 위치
- 배열 대비 장점
- 삽입 / 삭제 연산 이후 원소의 재배치가 필요 없다
- 메모리의 효율적인 사용 가능
📌 요세푸스 문제 (Josephus Problem)
-
1~N 까지 사람이 원을 이루며 앉아있다.
-
양의 정수 K (<= N)이 주어지고, 순서대로 K번째 사람을 제거
-
N명이 모두 제거될 때 까지 반복된다.
-
제거되는 순서를 출력하라.
-
List로 푸는게 이점이 크다. 배열보다
-
첫 병사 값을 음수 처리 후 이동
-
이동 시 병사의 값을 확인 하여 카운트
- 음수면 카운트 X
- 양수면 카운트+1
-
음수로 변한 병사의 명수 저장
-
남은 병사의 명수가 2라면 남은 병사의 인덱스 값 확인
-
배열의 문제점
-
배열 내 순환 횟수 증가
-
인원이 많아질 수록 순환 회수가 커져 시간이 오래 걸림
-
불필요한 연산 발생
- 계속해서 배열 값을 확인해야 한다. (확인 안하면 몇 번째 병사인지 구하는 것에 문제 생김)
-
-
-
List를 이용하자
-
노드를 생성하며, 각 노드에는 병사의 위치를 데이터로 저장
-
첫 병사를 삭제하고, 3만큼 이동
-
병사를 삭제하고 3만큼 이동
-
남은 병사 수가 2이면 각 병사의 데이터를 확인
-
List 이용 - 장점
-
불필요한 순회의 제거
- 죽은 병사가 삭제 처리되므로, 순회해야 하는 남은 병사의 수 감소
-
연산의 단순화
- 이동 후 삭제라는 간단한 연산만으로 문제 해결 가능
-
📌 삽입 정렬 (Insertion Sort)
- 자료 배열의 모든 원소들을 앞에서부터 차례대로 이미 정렬된 부분과 비교하여, 자신의 위치를 찾아냄으로써 정렬을 완성
✅ 정렬 과정
-
정렬할 자료를 두 부분집합 S와 U로 가정
- 부분집합 S : 정렬된 앞부분의 원소들
- 부분집합 U : 아직 정렬되지 않은 나머지 원소들
-
정렬되지 않은 부분집합 U의 원소를 하나씩 거내서 이미 정렬되어있는 부분집합 S의 마지막 원소부터 비교하면서 위치를 찾아 삽입한다.
-
삽입 정렬을 반복하면서 부분집합 S의 원소는 하나씩 늘리고 부분집합 U의 원소는 하나씩 감소하게 한다.
-
부분집합 U가 공집합이 되면 삽입정렬이 완성된다.
-
첫 pass에서는 비교가 한번 일어남
-
두번째 pass에서는 비교 두번
=> 원소가 N개 일때 N-1번의 pass, 각 pass마다 비교 N-1번
- 시간 복잡도 : O(N^2)
- {69, 10, 30, 2, 16, 8, 31, 22}를 삽입 정렬하는 과정
- 초기 상태 : 첫 원소는 정렬된 부분 집합 S로 생각하고 나머지 원소들은 정렬되지 않은 부분 집합 U로 생각한다.
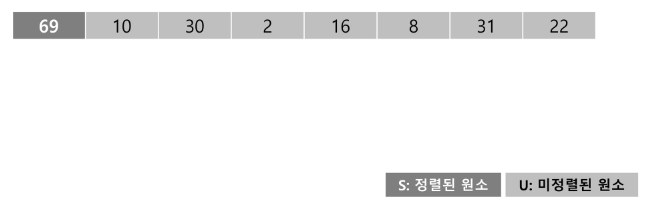
-
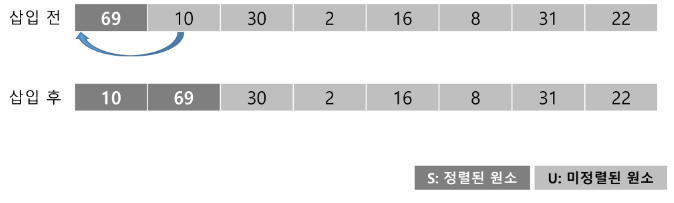
U의 첫 원소 10을 S의 마지막 원소 69와 비교할 때 10 < 69 이므로 원소 10은 69의 앞자리에 위치하게 된다.
-
더 이상 비교할 S의 원소가 없으므로 찾은 위치에 원소 10을 삽입한다.
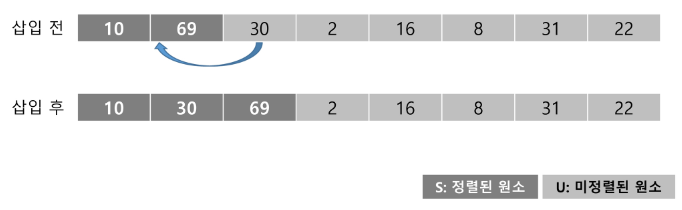
- U의 첫 원소 30을 S의 마지막 원소 69와 비교할 때, 30 < 69 이므로, 69의 앞자리 원소 10과 비교한다.
-
U의 첫 원소 2를 S의 마지막 원소 69와 비교할 때, 2 < 69 이므로, 69의 앞자리 원소 30과 비교한다.
-
비교를 반복하여 최종적으로 가장 앞자리에 삽입한다.
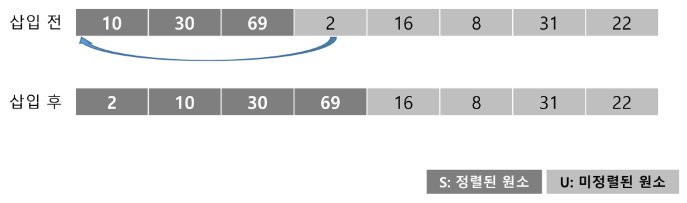
-
U의 첫 원소 16을 S의 마지막 원소 69와 비교할 때, 16<69이므로, 69의 앞자리 원소 30과 비교한다.
-
비교를 반복하여 10과 30 사이에 삽입한다.
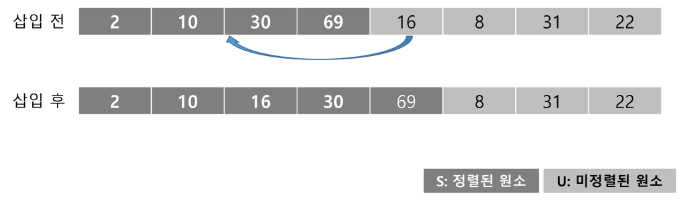
-
U의 첫 원소 8을 S의 마지막 원소 69와 비교할 때, 8<69이므로, 69의 앞자리 원소 30과 비교한다.
-
비교를 반복하여 2와 10 사이에 삽입한다.
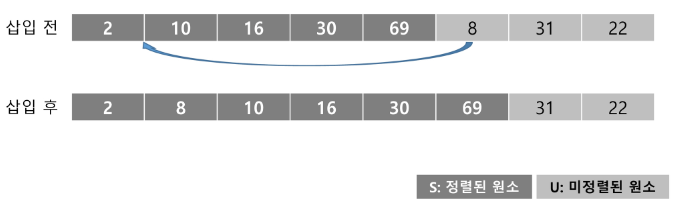
-
U의 첫 원소 31을 S의 마지막 원소 69와 비교할 때 31<69이므로, 69의 앞자리 원소 30과 비교한다.
-
비교를 반복하여 30과 69사이에 삽입한다.
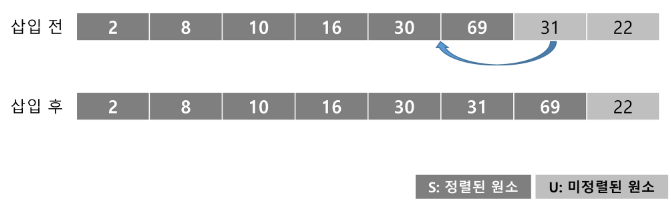
-
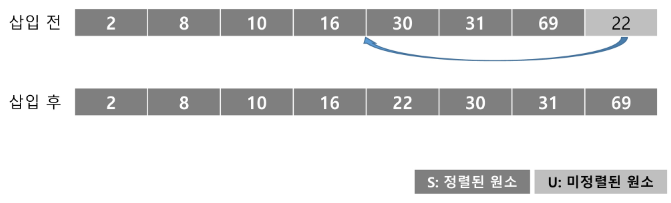
U의 첫 번째 원소 22을 S의 마지막 원소 69와 비교할 때, 22 < 69 이므로, 69의 앞자리 원소 31과 비교한다.
-
비교를 반복하여 16와 30 사이에 삽입한다.
✅ 다른 알고리즘 정렬들과의 비교