📖 List 1
📌 알고리즘
✅ 알고리즘
-
유한한 단계를 통해 문제를 해결하기 위한 절차나 방법이다.
-
주로 컴퓨터 용어로 쓰이며, 컴퓨터가 어떤 일을 수행하기 위한 단계적 방법을 말한다.
-
어떠한 문제를 해결하기 위한 절차
- 알고리즘 디자인 : 문제 해결 능력, 논리적 사고력
- 알고리즘 구현 : 객체지향 X, static 변수, 메서드 , 빠르고 간결하게, 표준 입출력, 테스트케이스
✅ 의사코드(pseudocode)와 순서도
-
의사코드(pseudocode) : 프로그래밍 언어를 흉내만 내는 코드
- 대부분의 경우 활용할 것
- 정해진 규칙이 없다!
- 반환형 X
- 접근제어자 X
- 타입 X -> 이름만
-
순서도
-
유연하지 않다.
-
✅ 알고리즘 성능
-
APS(Algorithm Problem Solving)의 목표 중 하나는 보다 좋은 알고리즘을 이해하고 활용하는 것
-
무엇이 좋은 알고리즘인가?
-
정확성 : 얼마나 정확하게 동작하는가?
- 테스트케이스가 다 맞는가
-
작업량 : 얼마나 적은 연산으로 원하는 결과를 얻어내는가?
-
메모리 사용량 : 얼마나 적은 메모리를 사용하는가
- 가끔은 시간을 메모리와 trade-off 할 때가 있다. (ex> IoT 환경)
-
단순성 : 얼마나 단순한가
5: 최적성 : 더 이상 개선할 여지없이 최적화되었는가
- 주어진 문제를 해결하기 위해 여러 다양한 알고리즘이 가능
- 어떤 알고리즘을 선택해야 할까?
- 알고리즘 성능 분석 필요
- 성능 분석의 기준으로 알고리즘의 작업량을 비교한다.
-
알고리즘의 작업량을 표현할 때 시간 복잡도로 표현한다.
-
시간 복잡도(Time Complexity)
- 실제 걸리는 시간을 측정
- 실행되는 명령문의 개수를 계산
✅ 빅 오 표기법
- 시간 복잡도 = 빅-오(O) 표기법
- 시간 복잡도 함수 중에서 가장 큰 영향력을 주는 n에 대한 항만 표시
- 계수(Coefficient)는 생략하여 표시
✅ 다양한 시간 복잡도의 비교
- 요소 수가 증가함에 따라 각기 다른 시간복잡도의 알고리즘은 아래와 같은 연산 수를 보인다.
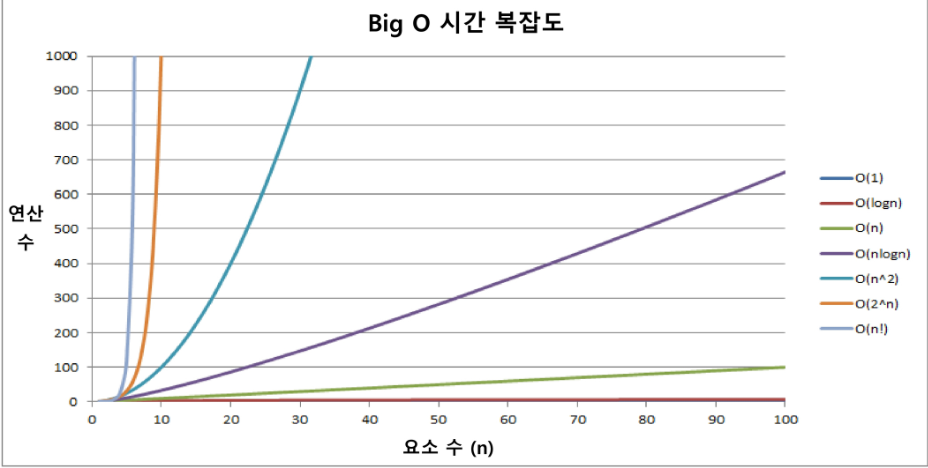
- n^2 : 최적화되지 않은 정렬 알고리즘
- nlogn : 최적화된 정렬 알고리즘
- 요소 수가 증가함에 따라 각기 다른 시간복잡도의 알고리즘은 아래와 같은 연산 수를 보인다.
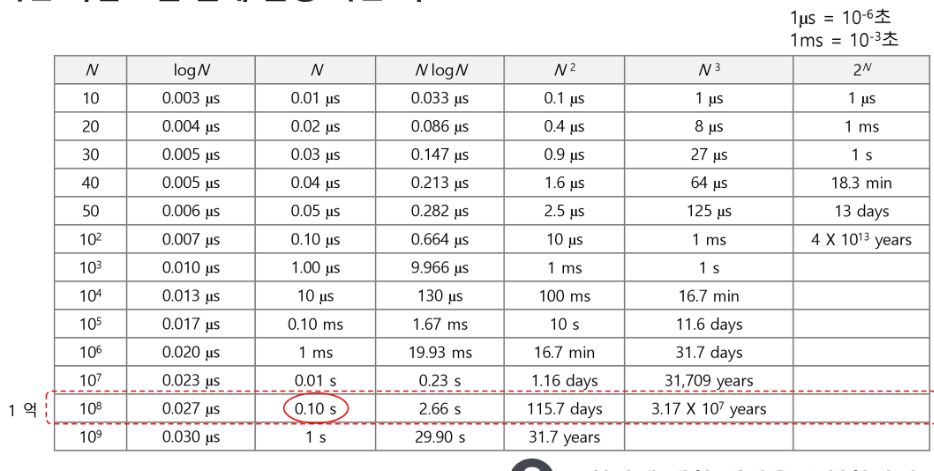
연산 10억 번 : 1초
📌 1차원 배열
✅ 배열
- 일정한 자료형의 변수들을 하나의 이름으로 열거하여 사용하는 자료구조
✅ 배열의 필요성
-
프로그램 내에서 여러 변수가 필요할 때, 일일이 다른 변수명을 이용하여 자료에 접근하는 것은 매우 비효율적일 수 있다.
-
배열을 사용하면 하나의 선언으로 둘 이상의 변수를 선언할 수 있다.
-
다수 변수로는 하기 힘든 작업을 배열을 활용해 쉽게 할 수 있다.
✅ 1차원 배열의 선언
-
자료형 : 배열을 이루는 자료형
-
이름 : 프로그램에서 사용할 배열 이름
-
길이 : 배열을 이루는 원소 수
int[] nums = new int[6]
✅ 1차원 배열의 접근
- nums[0] = 10; // 배열 nums의 0번째 원소에 10을 저장
- nums[idx] = 20; // 배열 nums의 idx번째 원소에 20을 저장
📌 정렬
✅ 정렬
-
2개 이상의 자료를 특정 기준에 의해 작은 값부터 큰 값(오름차순) 혹은 그 반대의 순서(내림차순)대로 재배열 하는 것
-
키 : 자료를 정렬하는 기준이 되는 특정 값
✅ 정렬 종류
-
버블 정렬 (Bubble Sort)
- O(N^2)
-
선택 정렬 (Selection Sort)
- O(N^2)
-
삽입 정렬 (Insertion Sort)
- O(N^2)
-
카운팅 정렬 (Counting Sort)
- O(N+k)
-
병합 정렬 (Merge Sort)
- O(NlogN)
-
퀵 정렬 (Quick Sort)
- O(N^2) => O(NlogN)
✅ 버블 정렬(Bubble Sort)
-
인접한 두 개의 원소를 비교하며 자리를 계속 교환하는 방식
-
정렬 과정
- 첫 원소부터 인접한 원소끼리 계속 자리를 교환하면서 맨 마지막 자리까지 이동한다.
- 한 단계가 끝나면(1st pass) 가장 큰 원소가 마지막 자리로 정렬된다. (마지막 pass : 숫자 2개가 정렬)
- 교환하며 자리를 이동하는 모습이 물 위에 올라오는 거품 모양과 같다고 하여 버블 정렬이라고 한다.
-
시간 복잡도
- O(N^2)
-
배열의 크기가 N -> pass는 최대 N-1번 (중간에 운으로 정렬이 다 되버릴 수도 있으므로 최대.)
-
비교의 경우 1pass : n-1회, 2pass: n-2회 ... n-1 pass : 1회
-> n(n-1)/2 => O(n^2)
✅ 배열을 활용한 버블 정렬
BubbleSort(int[] a, int N) { // a[] : 정렬할 배열, N : 배열의 크기
for i from N-1 to 0 decreasing by 1 { // pass가 몇 번 ? n-1
for j from 0 to i {
if(a[j] > a[j+1]) then {
temp <- a[j];
a[j] <- a[j+1];
a[j+1[ <= temp;
}
}
}
}int arr[5] = {3, 2, 8, 1, 4};
for(int i=0; i<arr.length-1; i++) {
for(int j=0 j<arr.length-i-1; j++) {
if(arr[j] > arr[j+1]) {
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
System.out.println(Arrays.toString(arr));
