[Algorithm] List 4 (02/16)

박세윤·2023년 2월 16일

Java algorithm

Algorithm

목록 보기

4/24

📖 List 4

📌 2차원 배열

✅ 2차원 배열의 선언

2차원 이상의 다차원 배열은 차원에 따라 Index 선언
세로길이 (행의 개수), 가로 길이 (열의 개수)를 필요로 함.

int[][] twoDimArr = new int[2][4];

✅ 배열 순회

nxm 배열의 n*m 개의 모든 원소를 빠짐 없이 조사하는 방법
행 우선 순회

int i; // 행의 좌표 => row
int j; // 열의 좌표 => col

for i from 0 to n-1
	for j from 0 to m-1
    	Arrays[i][j] // 필요한 연산 수행

열 우선 순회

int i; // 행의 좌표
int j; // 열의 좌표

for j from 0 to m-1
	for i from 0 to n-1
    	Array[i][j] // 필요한 연산 수행

지그재그 순회

int i; // 행의 좌표
int j; // 열의 좌표

for i from 0 to n-1
	for j from 0 to m-1
    	Array[i][j + (m-1-2*j)*(i%2)] // 인덱스가 홀수이면 역방향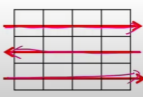

✅ 델타를 이용한 2차 배열 탐색

2차 배열의 한 좌표에서 4 방향의 인접 배열 요소를 탐색하는 방법

array[0 ... n-1][0 ... n-1] // 2차원 배열 [n][n]
dr[] <- {-1, 1, 0, 0} # 상하좌우
dc[] <- {0, 0, -1, 1}

for r in from 0 to n-1
	for c in from 0 to n-1
    	for d from 0 to 3
        	nr <- r + dr[d];
            nc <- c + dc[d];
            // 조건
            array[nr][nc]; // 필요한 연산 수행

✅ 전치 행렬

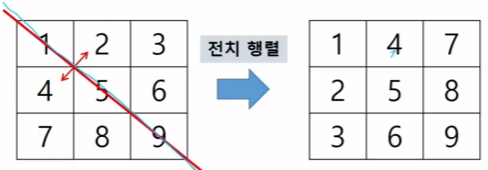
주 대각선을 기준으로 대칭하여 만든 행렬
지수 자리에 T (tranpose) 사용

arr = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}} // 3*3 행렬
int i; // 행의 좌표
int j; // 열의 좌표

for i from 0 to 2
	for j from 0 to 2
    	if(i<j)
        	swap(arr[i][j], arr[j][i]);

📌 카운팅 정렬 (Counting Sort)

✅ 카운팅 정렬

항목들의 순서를 결정하기 위해 집합에 각 항목이 몇 개씩 있는지 세는 작업을 하여, 선형 시간에 정렬하는 효율적인 알고리즘
제한 사항
- 정수나 정수로 표현할 수 있는 자료에 대해서만 적용 가능
- 각 항목의 발생 회수를 기록하기 위해, 정수 항목으로 인덱스 되는 카운트들의 배열을 사용하기 때문
- 카운트들을 위한 충분한 공간을 할당하려면 집합 내의 가장 큰 정수를 알아야 한다.
시간 복잡도
- O(N+K) : N은 배열의 길이, K는 정수의 최대값

✅ [0, 4, 1, 3, 1, 2, 4, 1]을 카운팅정렬 하는 과정

여기는 라이브 강의 다시보는거 추천

data에서 각 항목들의 발생 회수를 세고 정수 항목들로 직접 인덱스 되는 카운트 배열 counts에 저장함

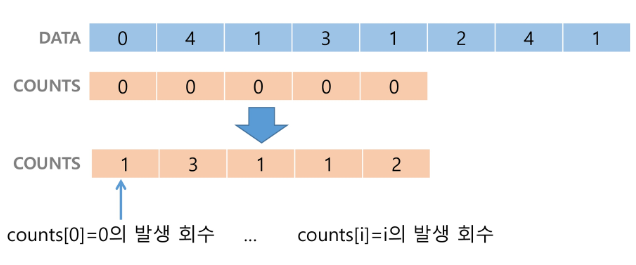
누적합(상대적 위치) 배열로 조정

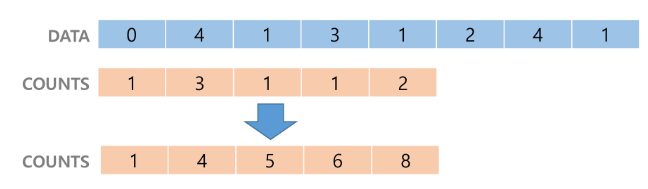
이 누적합 배열을 인덱스로 활용하려면 -1 해서 사용 (인덱스는 0부터니까)
사용하고 나서 누적합 배열 값 -1

//O(N+k)
Counting_Sort(A, B, K) 
// A[] -- 입력 배열
// B[] -- 정렬된 배열
// C[] -- 카운트 배열
// k -- 최대 값, n : 입력 뱅려 길이

C = new int[k];

// O(N)
for i from 0 to n
	C[A[i]] += 1; // 개수 세기

// O(k)
for i from 1 to k
	C[i] += C[i-1] // 누적 합

// O(N)
for i from n-1 to 0
	B[C[A[i]]-1] = A[i]
    C[A[i]] -= 1 // 누적합 배열 1 빼기

import java.util.Arrays;

public class 카운팅정렬 {
	// O(N+K)
	public static void main(String[] args) {
		int[] arr = {7, 1, 8, 66, 80, 66, 80, 66, 44, 65};
		
		int max = Integer.MIN_VALUE;
		
		// 최대값 찾기
		for(int i=0; i<arr.length; i++) {
			if(max < arr[i])
				max = arr[i];
		}
		
		// 카운팅배열 선언
		int[] cnt = new int[max+1];
		
		// 카운팅
		for(int i=0; i<arr.length; i++)
			cnt[arr[i]]++;
		
		// 카운팅배열 누적합화
		for(int i=1; i<cnt.length; i++)
			cnt[i] += cnt[i-1];
		
		int sortedArr[] = new int[arr.length];
		
		for(int i=0; i<arr.length; i++) {
			sortedArr[cnt[arr[i]] - 1] = arr[i];
			cnt[arr[i]]--;
		}
		
		System.out.println(Arrays.toString(sortedArr));
	}
}