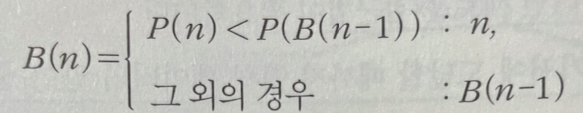1. 반복 전략
반복 전략은 루프(for, while등의 반복문)속에서 조건이 충족될 때 까지 절차를 반복하는 것이다.
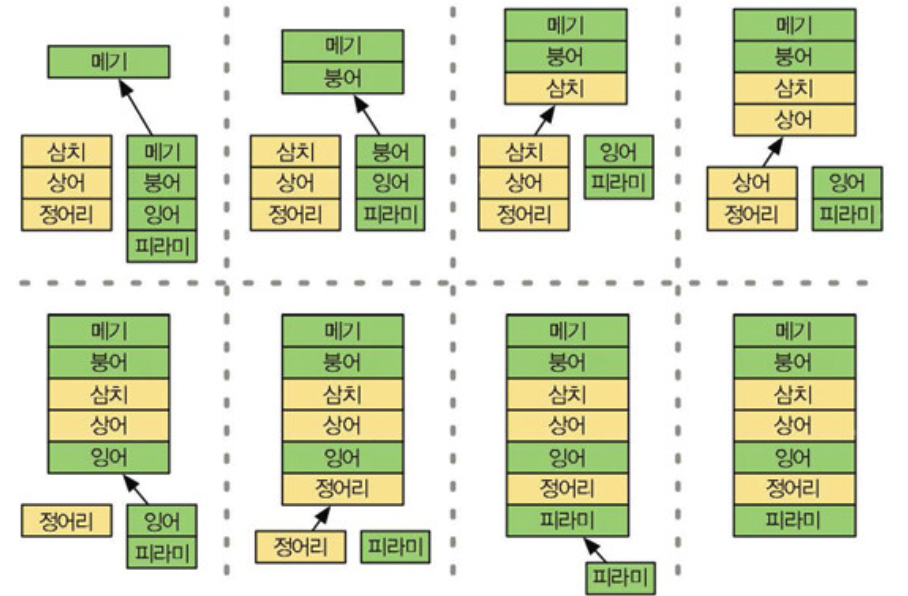
🐠 물고기 리스트 합치기
바닷물고기 리스트와 민물고기 리스트가 각각 가나다순으로 정렬되어 있을때 물고기 전체의 가나다 순 리스트를 구시오.
def merge(sea, fresh): fish=[] while not(len(sea)==0 and len(fresh)): if max(sea) > max(fresh): fish.append(sea.pop()) else: fish.append(fresh.pop()) return fish
- 이렇게 두 리스트를 합치는 것을 병합 알고리즘이라고 한다. 물고기 이림 개수에 따라 연산 비용이 선형적으로 증가하므로 병합 알고리즘의 시간 복잡도는 O(n)이다.
1-1) 중첩루프와 멱집합
멱집합이란 어떤 집합의 원소로 만들 수 있는 모든 부분집합을 뜻한다.
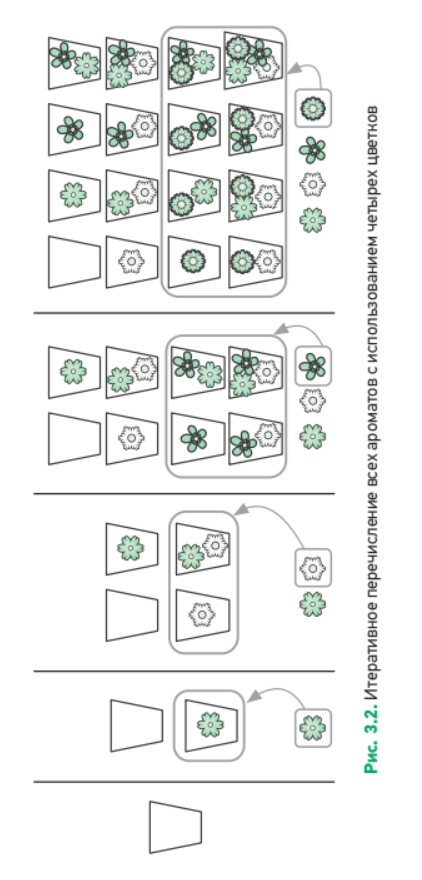
💐 향 조합하기
꽃에서 추출한 향을 조합하여 새로운 향을 만들고자 한다. 꽃의 집합 F가 있을 때 조합할 수 있는 모든 향의 목록을 구하시오.
def powerSet(flowers): result=[[]] for i in flowers: newList=result.copy() for j int newList: j.append(i) result += newList return result
- 꽃을 하나 추가할 때마다 만들 수 있는 향은 두배씩 증가한다. 이것은 지수적 증가 (2**(k+1) = 2*2**k)를 뜻한다. 이처럼 입력항목이 하나 증가할 때마다 필요한 연산이 두배로 증가하는 알고리즘은 지수 알고리즘이다. 그리고 지수 알고리즘의 시간 복잡도는 O(2**n)이다.
- 멱집합을 생성하는 것은 진리표를 생성하는 것과 같다. 각각의 꽃을 진리표의 논리 변수라고 생각하면, 변수의 True/False 조합으로 향의 조합을 표현할 수 있다.
1-2) 재귀를 이용해 반복하기
재귀란 어떤 함수가 자기 자신이나 자신의 복제본에 작업을 전파하는 것이다. 재귀 알고리즘은 자기 자신을 처리하는 문제를 다룰 때 사용한다.
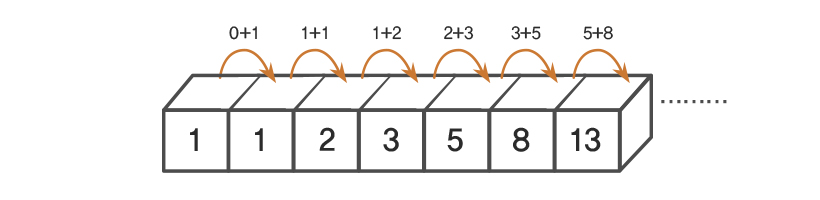
🧮 피보나치 수열
처음 두개의 숫자로 시작하여 이어지는 수는 이전의 두 수의 합을 구하시오.
def fibo(n): if n<=2: return 1 return fibo(n-1)+fibo(n-2)
- 재귀를 이용하면 알고리즘을 직관적이고 간결하게 작성할 수 있다. 재귀를 적용하기 위해서는 문제를 '그 자신'이라는 개념으로 정의할 수 있어야 한다.
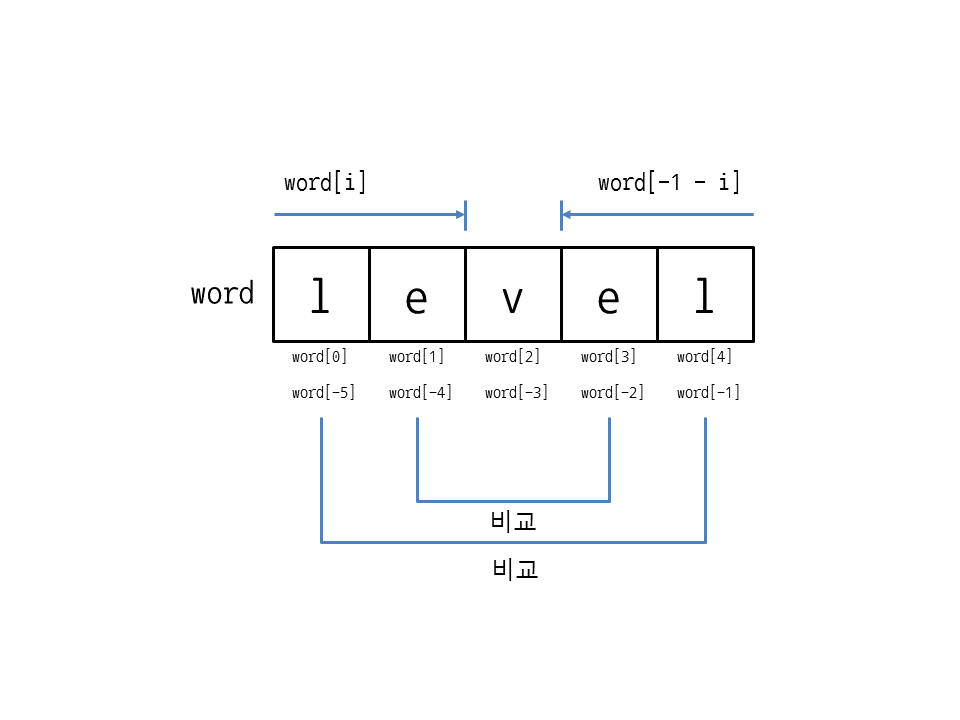
📄 회문 검사
단어를 역순으로 뒤집었을 때 원래 단어와 달라지는지 구하시오.
def palindrome(word): if len(word) <= 1: return True elif word[0] != word[-1]: return False w=del word[0] w=del word[-1] return palindrome(w)
- 재귀 알고리즘에는 기저(base case)가 존재한다. 기저란 입력데이터가 더 이상 작아질 수 없는 경우로, 재귀적 호출이 끝나는 지점이다. fibo알고리즘의 기저는 수1과 수2이고, palindrome알고리즘의 기저는 무자가 1개 또는 0개인 단어이다.
1-3) 재귀와 반복의 비교
- 재귀 알고리즘의 장점 : 반복 알고리즘에 비해 간결하다.
- 재귀 알고리즘의 단점 : 재귀 알고리즘이 실행되면 수많은 자기복제본이 만들이지고, 계산 비용이 별도로 발생한다. (완료되지 않은 재귀 호출과 중간계산 과정을 계속 추적해야하기 때문이다.)
- 해소 : 성능을 최대한 높여야 하는 상황이라면 재귀 알고리즘을 순수한 반복형태로 수정해서 추가 비용이 발생하지 않도록 하면 된다.
- 정리 : 재귀로 작성한 알고리즘은 모두 반복 알고리즘으로 바꿀 수 있다.
반복형태로 작성한 코드는 재귀 코드보다 일반적으로 실행속도가 더 빠르지만, 더 복잡하고 이해하기 어렵다.
2. 완전 탐색(브루트 포스)
답이 될 수 있는 후보를 전부 조사하여 문제를 해결하는 방법이다.
💵 최적 거래 문제
일정기간 동안의 금 가격이 주어져 있다. 이 기간 중 며칠에 금을 사고 며칠에 금을 팔았을 때 이윤을 최대화 할 수 있는지 알고 싶을 때 금을 사고 파는 최적의 두 날짜를 구하시오.
- 쉽게 생각하면 최저가에 사서 최고가에 파는 날을 구하면 된다. 하지만 최저가에 사서 최고가에 파는 것이 불가능한 경우도 있다. 가격이 최고가를 찍은 후 최저가로 내려간 경우 시간을 거스를 수 없기 때문이다.
- 완전 탐색은 가능한 날짜 쌍을 모두 구해 답을 찾는다. 일정 기간동안 날짜 상의 수는 기간이 증가함에 따라 이차식으로 증가한다. 따라서 이경우 시간 복잡도는 O(n**2)이다.
- 이문제의 경우 완전탐색으로 풀면 지수 시간 복잡도를 가지므로 비효율적이다. 그러나 경우에 따라서는 완전 탐색이 최선인 경우도 있다.
👝 배낭 문제
한 상인이 상품을 배낭에 골라 담아, 시장에 내다 팔려 한다. 각 상품의 무게와 가치가 주어져 있으며, 배낭에는 상품을 일정한 무게까지만 담을 수 있다. 배낭에 상품을 담아갈 기회는 단 한 번이다. 배낭에 담은 상품의 가치를 가장 높게 하려면 어떤 상품들을 골라야 하는가?
- 전체 상품의 모든 조합을 구하려면 멱집합을 구하면 된다. 멱집합을 구한 뒤 완전탐색 전략에 따라 각 상품 조합의 총 무게와 판매가를 하나씩 확인다. 각각의 조합마다 무게의 합이 배낭의 용량을 넘는지 그리고 가격의 합이 이전 최고가 보다 높은지 검사한다.
- 이 알고리즘은 상품이 n개 일 때 가능한 상품 조합은 2**n이다. 각각의 조합마다 고정된 횟수만큼 용량 초과 여부, 최고가 갱신 여부를 검사하므로, 시간 복잡도는 O(2**n)임을 알 수 있다.
3. 역추적(백트래킹)
완전 탐색의 불필요한 탐색을 줄여 효율성을 높인 해결 방법이다.
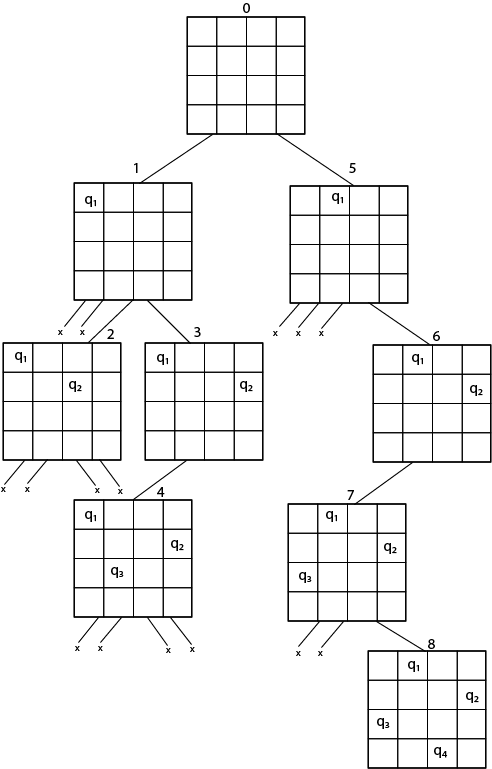
♟ 여덟 퀸 문제
체스판 위에 여덟 개의 퀸을 서로 공격할 수 없도록 배치하시오.
- 첫 번째 퀸은 어디에 두더라도 괜찮다. 하지만 그 다음 퀸을 둘 수 있는 자리는 이전에 둔 퀸에 의해서 제한된다. 다른 퀸의 공격 범위에 퀸을 두는 경우 나머지를 옳게 배치하더라도 의미가 없다. 이런 경우의 수를 지우고 이전으로 돌아가서 다시 탐색을 이어나간다.
- 문제에서 구하고자 하는 답이 선택의 연속이고, 앞에서 한 선택이 그 뒤의 선택을 제한한다면 역추적 전략을 사용하기 좋다.
- 역추적 전략은 어떤 선택이 정답이 되지 못한다는 것을 빠르게 파악한다. 잘못된 길에서 재빨리 발을 빼고, 다른 선택지를 시도할 수 있는 것이다.
- 일찍 실패하고, 자주 실패하기!
4. 발견법(휴리스틱)
직관에 의해서 최고의 수는 아니더라도 충분히 좋은 수를 찾는 방법이다. 완전 탐색이나 역추적 전략 사용시 시간이 너무 많이 걸릴 때 사용한다.
4-1) 탐욕법
이전의 선택으로 절대 돌아가지 않는다. 각 단계마다 최선의 선택을추구하되, 일단 선택하고 나면 과거의 선택을 되돌아보지 않는 것이다.
👝 배낭문제(난이도: 상)
탐욕스러운 절도범이 당신의 집에 숨어들어 상품을 훔쳐가려한다. 절도범은 훔친 물건을 당신의 배낭에 담아갈 생각이다. 집에 머물러 있는 시간이 짧을수록 잡힐 확률도 줄어든다고 할 때, 어떤 물건을 훔쳐가는 것이 좋을지 구하시오.
- 탐욕스러운 절도범은 더 이상 물건을 담을 수 없을 때까지 가장 가치가 높은 물건부터 순서대로 배낭에 담는다. 이렇게 구한 조합이 반드시 최고가라는 보장은 없지만 완전 탐색이나 역추적 보다 훨씬 빠르게 조합을 구할 수 있다.
4-2) 탐욕이 힘을 얻는 순간
완벽한 답을 구하는 전통적인 알고리즘 대신 발견법을 선택한다면 답을 빨리 구할 수 있겠지만 정확성이 떨어지는 점을 감수해야한다. 그러나 작금의 선택이 미래에 영향을 끼치지 않는 경우에는 탐욕법과 완전탐색으로 얻은 값이 일치한다.
🔌 전력망 연결
전력이 연결되지 않은 여러 마을에 전력을 공급하고자 한다. 그 중 한 마을에 발전소를 건설하고 있다. 전깃줄을 가장 적게 들여서 모든 마을에 전력을 어떻게 연결해야 좋은지 구하시오.
5. 분할정복
이 전략은 최적 부분 구조로 구성된 문제를 해결하기에 적합하다. 최적 부분 구조로 구성된 문제란 비슷한 형태의 더 작은 부분 문제로 문제를 나눌 수 있는 문제이다. 이렇게 나뉜 부분 문제 역시 같은 방식으로 계속 나눌 수 있다. 계속 나누다 보면 결국 쉽게 풀 수 있는 간단한 문제가 된다. 이 간단한 문제들의 답을 각각 구한 뒤 서로 결합하면 원래 문제의 답을 구할 수 있다.
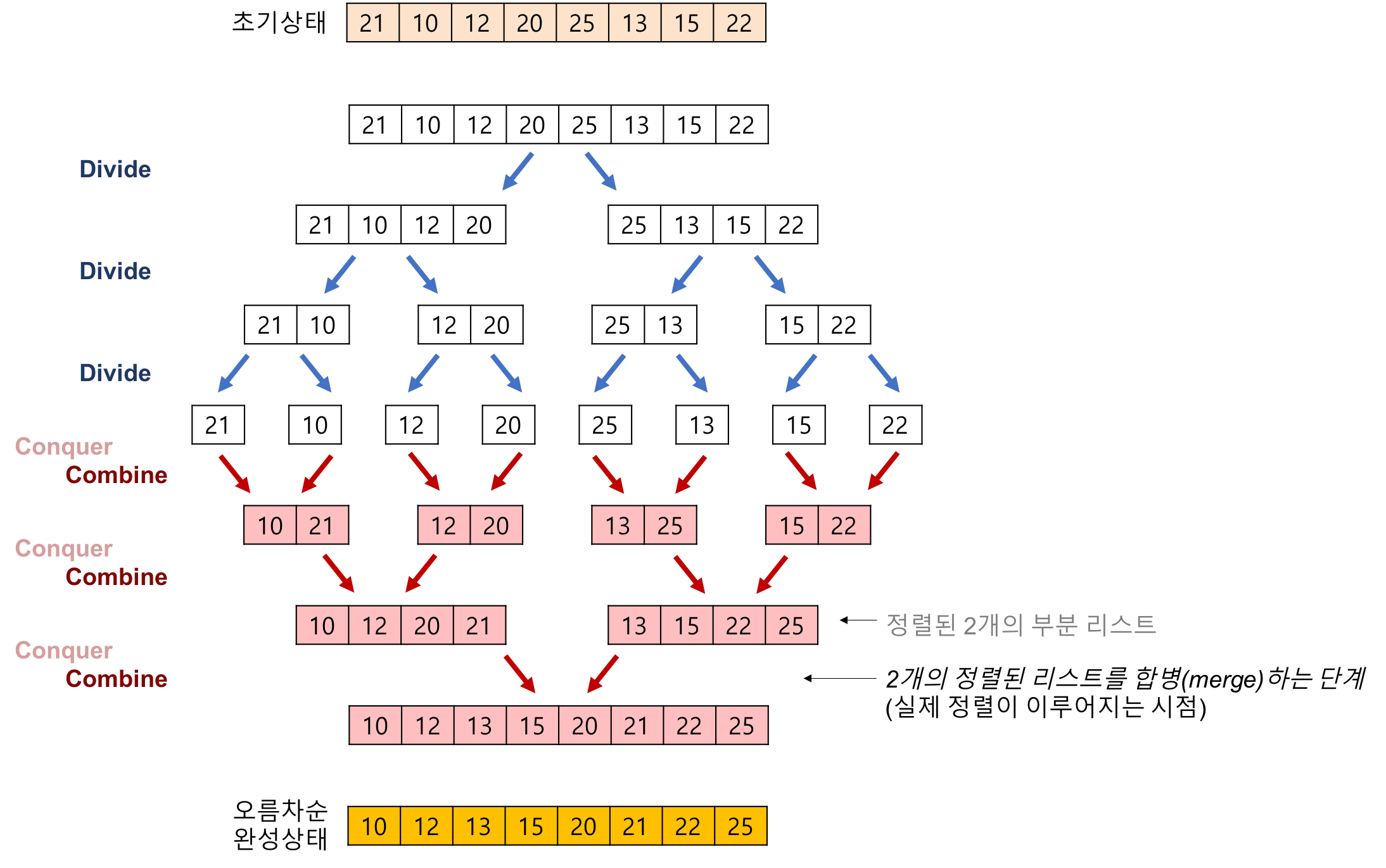
분할 정렬
def merge_sort(list): if len(list) = 1: return list left = list[:len(list)//2+1] right = list[len(list)//2+1:] return merge(merge_sort(left), merge_sort(right))
- 위의 재귀 알고리즘은 병합 정렬이라고도 부른다. 병합 정렬의 시간 복잡도는 몇일까? 이를 알기 위해서는 먼저 각 분할 단계에서 발생되는 연산 횟수를 구해야한다. 그 후 전체에서 발생하는 분할 단계가 몇 차례인지도 세어야 한다.
- 항목의 개수가 n개인 큰 리스트가 있다고 하자. 이 리스트에 대해 merge_sort함수를 호출하면 다음과 같은 연산이 실행된다.
- 리스트를 절반으로 나누는 작업 : 항목 개수 상관 없이 O(1)
- 병합 : O(n)
- 지배적 항(가장 빠르게 증가하는 항)만을 고려할 것이고, 재귀 호출은 세지 않는다. 따라서 이 함수의 시간 복잡도는 O(n)이다.
- 각 분할 단계에서 시간 복잡도는 항목의 개수에 상관이 없다고 했으니 모두 O(n)이다. 따라서 병렬 정렬의 시간 복잡도는 x*O(n)이다.(x:분할 단계 수)
- 그렇다면 x는 어떻게 구할까? 재귀 함수의 호출은 기저에 이르렀을 때 중단된다. 병합 정렬의 경우 기저는 항목이 하나뿐인 리스트이다. 또한 x단계의 분할이 n/2**x개 항목의 리스트에 해당한다.(계속 절반으로 나뉘니까)
- 따라서 x는 (n/w**x=1 >> 2**x=n >> x=long2n)으로 유도된다. 이를 종합하면 병렬 정렬의 시간 복잡도는 O(nlong2n)이다. 선택 정렬의 O(n**2)에 비하면 비교가 안될 정도로 효율적이다.
💵 최적거래(분할 정복)
달러 사고 팔아서 이익 극대화 하는 문제
- 날짜별 가격 목록을 절반으로 나누어 앞쪽 절반과 뒤쪽 절반에서 각각 최적 거래를 찾는 두 개의 부분문제로 나눈다. 이렇게 나누면 전체 기간 동안 최적 거래는 다음 세 답 중 하나가 된다.
1. 앞쪽 절반에서 사고 파는 최적거래
- 뒤쪽 절반에서 사고 파는 최적거래
- 앞쪽 저반에서 사고 뒤쪽 절반에서 파는 최적거래
- 이 문제의 기저는 기간이 단 하루인 경우이다. 같은 날 사고 팔면 이윤이 0이기 때문이다.
- n개의 항목에서 최댓값과 최솟값을 구하려면 n개 항목 모두를 살펴야 하므로 trade함수 독립적 호출 비용은 O(n)이다. O(n)의 비용이 드는 재귀 트리를 log2n회 분할 단계를 수행한다.
👝 배낭 문제(분할 정복)
n가지 상품 중에서 가치 있는 것을 골라 담는 문제
wi : i번째 상품 무게
vi : i번째 상품 가치
c : 배냥 용량
i : 상품 번호
n : 상품 개수
(k(n,c) : n가지 상품 중 골라 담을 수 있는 최대 가치)
- 새로운 상품 i=n+1이 추가될 때마다 배낭에 담을 수 있는 최대 가치는 증가할 수도 있고, 아닐수도 있다. 즉 다음 두 경우 중 가치가 더 높은 경우가 된다.
1. k(n,c) : 새 상품이 선택되지 않는 경우
- k(n,c-wi+1)+vn+1 :새 상품이 선택되느 경우
- 단점 : 동일한 부분 문제가 여러번 반복해서 계산된다.
6. 동적 계획법
문제를 풀 때, 동일한 연산이 여러 차례 수행되는 경우가 있다. 동적 계획법을 활용하면 반복되는 부분 문제를 식별하여 이들을 한 번씩만 연산할 수 있다. 이를 위해 메모이즈라는 기법을 활용한다.
🧮 피보나치 수열(동적 계획법)
- fibo함수는 계산을 숳애하기 전에 계산된 결과가 저장되어 있는지 먼저 확인한다. 계산 결과가 저장되어 있다면 그 값을 꺼내 반환하고, 계싼 결과가 없을 때만 계산을 수행하여 결과를 저장한 후에 반환한다.
- 그러면 함수가 동일한 입력으로 여러번 호출되더라도 실제 계산은 한 번씩만 수행한다. 이렇게 부분 계산 결과를 저장해두었따가 재사용하는 기법을 메모이제이션이라 한다.
- 동적 계획법을 활용하면 형편없이 느린 프로그램을 제법 쓸만한 속도로 개선할 수 있다. 이를 위해서는 알고리즘에서 반복적으로 계산된느 부분이 없는지 주의 깊게 분석해야 한다.
상향식 접근법
지금까지는 기저에 도달할 때가지 입력 데이터의 양이 줄어들도록하는 하향식 접근법에 의존했다. 하지만 반대로 기저 사례를 먼저 계산한 뒤 부분 계산 결과들이 최종 정답에 도달할 때까지 조합해서 나가는 상향식 접근법으로 문제를 풀수도 있다.
💵 최적 거래(상향식 접근법)
P(n) : n번째 날의 가격
B(n) : n번째 날에 팔 물건을 가장 저렵ㅎ게 살 수 있는 날
P(2) < P(1) ➡️ B(2)=2 (둘째 날에 사고 판다.)
P(2) >= P(1) ➡️ B(2)=1 (첫째 날에 사고, 둘째 날에 판다.)
P(3) < B(2)번째 날의 가격 ➡️ B(3)=3
P(3) >= B(2)일의 가격 ➡️ B(3)=B(2)
- 셋째 날이 도기 전의 기간에서 최저 가격을 기록하는 날은 B(2)이다. 따라서 B(3)는 다음 중 하나이다.
- 마찬가지로 넷째 날이 되기전에 최저 가격을 기록하는 날은 B(3)이다.
- 즉, 모든 n에 대하여 n번째 날이 되기 전의 최저 가격은 B(n-1)이다. 이를 이용해서 B(n)을 B(n-1)에 관한식으로 나타낼 수 있다.
7. 분기 한정법
최적화 문제에서 구하려는 답이 '선택의 연속'일 때 자주 활용되는 전략이다. 나쁜 선택지를 빠르게 제거해서 시간을 절약할 수 있다.
상한과 하한
문제를 풀다보면 '차선의 답'을 쉽게 구할 수 있을 때가 많다. 이런 답은 최적해에 다가가는 범위를 설정한다. 차선의 답보다 안좋으면 버리고 차선의 답보다 좋은 경우로 범위를 좁혀 나간다.
- 단계 - 문제를 여러 개의 부분 문제로 나눈다.
- 단계 - 각 부분 문제의 상한과 하한을 구한다.
- 단계 - 각 부분 문제에서 모든 분기의 상한, 하한 범위를 비교한다.
- 단계 - 가장 유망한 부분 문제를 선태갛여 1단계로 돌아간다.
참조