Analysis of Algorithm
time complexity
- best-case : 가장 좋은 데이터가 입력된 경우
- average-case : 모든 데이터에 대한 평균
- worst-case : 가장 최악의 데이터가 입력되었을 경우
space complexity
- 입력 데이터를 저장하는 메모리 양은 제외
- 알고리즘에서 추가적으로 사용하는 메모리 양
Stability of Sorting Algorithm
Stable sorting algorithm

- 크기가 같은 데이터가 정렬된 이후에도 입력된 순서를 그대로 유지하게 하는 정렬 알고리즘
- YES
- Merge
- Insertion
- Bubble
- Cocktail Shaker
- No
- Quick
- Heap
- Selection
- Shell
- Exchange
- Comb
- YES
In-Place Algorithm
- 입력 데이터를 저장하는 메모리 이외는 상수 크기의 메모리만 필요한 알고리즘
- 알고리즘 중간 계산에 필요한 변수 등에 필요한 메모리
Term
Pass

- 정렬 알고리즘에서 반복적으로 수행되는 비교 및 교환의 한 단계
Gap

- 정렬할 원소들이 떨어져 있는 거리
Gap Sequence
- 주어진 시작 숫자부터 gap 만큼 떨어진 모든 숫자들의 집합
Input
3
9 1 2 3 4 5 6 7 8 9
9 9 8 7 6 5 4 3 2 1
9 9 6 3 1 2 4 5 7 8Bubble Sort
: 인접한 두 숫자를 비교하여 두 수의 정렬순서가 맞지 않는 경우에 교환
- Stable
- In-place
basic
- 비교 연산자 총 실행 횟수 : n(n-1)/2
- 0번째 부터 n
void bubbleSort(int a[], int n)
{
int countCmpOps = 0;
int countSwaps = 0;
for (int i=0; i<n-1; i++) {
for (int j=0; j<n-i-1; j++) {
countCmpOps++;
if (a[j+1] < a[j]) {
countSwaps++;
swap(a[j+1], a[j]);
}
}
}
printf("%d %d ", countCmpOps, countSwaps);
} 36 0
36 36
36 15improvement1
- 직전 pass에서 교환이 수행되지 않았으면 데이터가 정렬되어있다는 의미
- best case
- 입력 데이터가 오름차순으로 정렬되어 있는 경우
- 비교 연산자 총 실행 횟수 : n-1
- worst case
- 입력 데이터가 내림차순으로 정렬되어 있는 경우 + a
- 비교 연산자 총 실행 횟수 : n(n-1)/2
void bubbleSortImproved1(int a[], int n)
{
int countCmpOps = 0;
int countSwaps = 0;
bool swapped;
for (int i=0; i<n-1; i++) {
swapped = false;
for (int j=0; j<n-i-1; j++) {
countCmpOps++;
if (a[j+1] < a[j]) {
countSwaps++;
swap(a[j+1], a[j]);
swapped = true;
}
}
if (swapped == false) {
break;
}
}
printf("%d %d ", countCmpOps, countSwaps);
} 8 0
36 36
26 15improvement2
- 직전 pass에서 교환을 수행한 마지막 위치 이전까지만 비교를 수행
- 이전 pass에서 마지막으로 교환한 위치 이후는 정렬되어있다는 의미
void bubbleSortImproved2(int a[], int n)
{
int countCmpOps = 0;
int countSwaps = 0;
int lastSwappedPos = n-1;
int swappedPos;
while(lastSwappedPos) {
swappedPos = 0;
for (int j=0; j<lastSwappedPos; j++) {
countCmpOps++;
if (a[j+1] < a[j]) {
countSwaps++;
swap(a[j+1], a[j]);
swappedPos = j;
}
}
lastSwappedPos = swappedPos;
}
printf("%d %d ", countCmpOps, countSwaps);
} 8 0
36 36
20 15C++ 컴파일러는 함수 선언(prototype)이 함수 호출보다 먼저 나와야 하는 C 언어의 규칙을 따르지 않아도 됩니다. 이러한 특징을 "전방 선언" 또는 "함수 프로토타입"이라고 합니다. 함수의 정의(implementation)는 함수 호출보다 아래에 있어도 상관없습니다.
따라서 코드에서
swap함수의 선언이 호출보다 아래에 있어도 문제없이 동작합니다. 컴파일러는 함수 호출 시 해당 함수의 프로토타입(선언)을 찾아서 컴파일합니다. 때문에 함수의 정의가 프로토타입보다 나중에 나와도 컴파일러는 정상적으로 동작합니다.이러한 특징은 코드의 가독성을 높일 수 있으며, 관련 함수를 한데 모아 두지 않아도 되므로 큰 프로젝트에서 유용합니다. 함수의 구현을 코드의 다른 부분과 더 관련성 있게 배치할 수 있습니다.
Cocktail Shaker Sort
- Bidirectional bubble sort
- bubble sort의 단점 개선
- 거북이 데이터를 빠르게 제 위치로 이동시킴
- bubble sort의 각 pass를 양방향으로 번갈아가면서 수행
- worst case : O(n^2)
- 입력데이터가 많이 정렬되어 있는 상태라면 빠르게 정렬 가능
- 모든 숫자가 최종 위치에서 최대로 k(k≥1)만큼 떨어져 있는 경우 O(kn)
Comb Sort
- bubble sort의 단점 개선
- gap의 크기를 1보다 크게
- 각 pass가 진행될 때 마다 gap의 크기를 “shrink factor” k만큼 줄여감
- gap : n / (k^pass)
- 권장되는 k 값 : 1.3
- Not Stable
- In-place
void combSort(int a[], int n) {
int countCmpOps = 0;
int countSwaps = 0;
int gap = n;
float shrink = 1.3;
bool sorted = false;
while (!sorted) {
gap = gap / shrink;
if (gap <= 1) {
gap = 1;
sorted = true;
}
int i = 0;
while (i + gap < n) {
countCmpOps++;
if (a[i] > a[i + gap]) {
countSwaps++;
swap(a + i, a + i + gap);
}
i++;
}
}
printf("%d %d\n", countCmpOps, countSwaps);
}29 0
29 6
37 7Selection Sort
: 오른쪽 데이터에서 가장 작은 값을 오른쪽 데이터의 첫번째 값과 교환
- 왼쪽 : 정렬된 데이터
- 오른쪽 : 정렬되지 않은 데이터
- O(n(n-1)/2)
-
Not Stable

-
In-place
void selectionSort(int a[], int n)
{
int countCmpOps = 0;
int countSwaps = 0;
int minIndex = 0;
for (int i=0; i<n-1; i++) {
minIndex = i;
for (int j=i+1; j<n; j++) {
countCmpOps++;
if (a[minIndex] > a[j]) {
minIndex = j;
}
}
if (minIndex != i) {
swap(a + i, a + minIndex);
countSwaps++;
}
}
printf("%d %d\n", countCmpOps, countSwaps);
}Insertion Sort
: 오른쪽 데이터를 순서대로 왼쪽의 정렬된 데이터의 올바른 위치에 삽입
- 왼쪽 : 정렬된 데이터
- 오른쪽 : 정렬되지 않은 데이터
- Stable
- In-place
- Best case
- : 입력 데이터가 정렬된 경우
- O(n-1)
- Worst case
- : 입력 데이터가 역순으로 정렬된 경우
- O(n(n-1)/2)
void insertionSort(int a[], int n)
{
int countCmpOps = 1;
int countSwaps = 0;
for (int i=0; i<n-1; i++) {
for (int j=i; j>=0 && countCmpOps++ && a[j] > a[j+1]; j--) {
countSwaps++;
swap(a + j, a + j + 1);
}
}
printf("%d %d\n", countCmpOps-1, countSwaps);
}Shell Sort
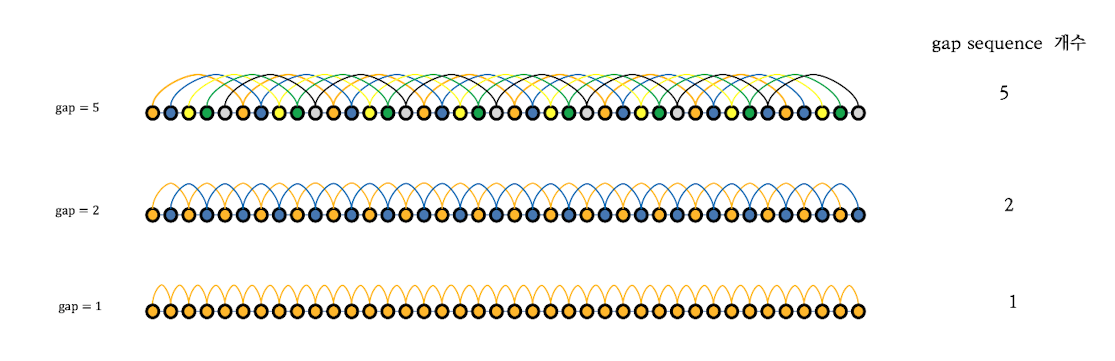
: 같은 gap을 가지는 모든 gap sequence에 insertion sort를 수행
- gap=1이 되면 insertion sort를 수행하는 것과 동일함
- gap>1에서 거북이 데이터를 목표 위치로 많이 이동시켜 놓았으므로 정렬된 상태에 가까운 상태에서 insertion sort를 수행 가능
- 각 pass가 진행될 때 마다 gap의 크기를 “shrink factor” k만큼 줄여감
- gap : n / (k^pass)
- 권장되는 k 값 : 2
- Not Stable
- In-place
void ShellSort(int a[], int n)
{
int countCmpOps = 1;
int countSwaps = 0;
int shrinkRatio = 2;
int gap = n / shrinkRatio;
int tmp, j, i;
while (gap > 0) {
for (i=0; i<n; i++) {
tmp = a[i];
for (j=i; j-gap>=0 && countCmpOps++ && tmp < a[j-gap]; j-=gap) {
countSwaps++;
a[j] = a[j - gap];
}
a[j] = tmp;
}
gap /= shrinkRatio;
}
printf("%d %d\n", countCmpOps-1, countSwaps);
}20 0
22 8
23 7
