[알고리즘] UPSKILL : Javascript 코딩테스트 131개 예제 & CS지식으로 끝내기(1)

최유나·2025년 7월 21일
Big O로그 시간 복잡도버블 정렬병합 정렬빅오표기법상수 시간 복잡도시간복잡도알고리즘힙 정렬
0

알고리즘

목록 보기
1/1

✅코딩 테스트

  1. 프로그래밍 언어 선택
  2. 유형별로 10개 이상 풀어보기
  3. 대표 알고리즘 유형 : 정렬, DFS/BFS, 구현, 완전 탐색, 탐욕 알고리즘
  4. 기업 기출 문제 풀기

✅시간 복잡도

  • 크기 형태의 의미, 수학적, 수치
  • 알고리즘의 성능을 나타내는 척도(얼마나 빠르게 수행되는가)
  • 시간 복잡도 : 특정한 크기의 입력에 대해 알고리즘 수행 시간 분석(낮아야 빠름)
    조금더 값이 크게 증가하는 정도, 수치적으로 값이 얼마나 큰가
  • 복잡도가 낮을수록 우수한 코드

✅시간 복잡도 표기법

빅오 표기법 (Big O Notation= 나타낸다)

  • 가장 빠르게 증가하는 항만 고려하는 표기법
  • 함수의 상한(가장 작은 수) 나타냄
  • 3N³+ 5N² +1,000,000
  • ² = 차수
  • N³ = 100 100 100 = 1000000
  • N이 급격하게 커지는 것에 비해 다른 항들에 대해선 영향이 작다
  • Big-O : 차수가 가장 큰 항에서 계수를 제외하여 O(N³)으로 표기

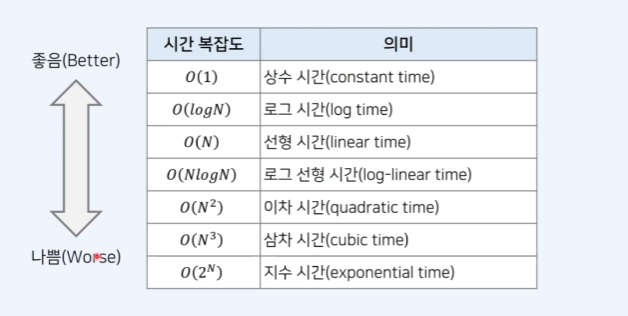
시간 복잡도의미 (한글/영문)설명
O(1)상수 시간 (constant time)입력 크기와 무관하게 항상 같은 시간. 가장 빠름. ex) 배열 인덱스로 접근
O(log N)로그 시간 (log time)입력이 커져도 천천히 증가. 이진 탐색 등에서 등장
O(N)선형 시간 (linear time)입력 크기만큼 실행 시간 증가. ex) 배열 전체 순회
O(N log N)로그 선형 시간 (log-linear time)병합 정렬(Merge Sort)이나 퀵 정렬 평균 시간
O(N²)이차 시간 (quadratic time)중첩 루프. ex) 버블 정렬, 브루트포스 2중 반복
O(N³)삼차 시간 (cubic time)3중 루프. ex) 플로이드-워셜 알고리즘 등
O(2^N)지수 시간 (exponential time)입력이 조금만 커져도 실행 시간이 폭증. 피해야 함. ex) 모든 부분 집합 찾기

🌍상수 시간 복잡도

사칙연산

🌍로그 시간 복잡도

절반씩 쪼갤때(이분 탐색), 상수 시간에 가까울 정도로 빠름

이분 탐색 (Binary Search)
정렬된 리스트나 배열에서 특정 값의 위치를 찾는 알고리즘

🌍선형 시간 복잡도

배열 하나씩 확인해서 어떤 원소가 존재하는지 찾을 때 사용(병합, 힙정렬...기반 알고리즘)

병합 정렬 (Merge Sort)

분할 정복 (Divide and Conquer)
병합 정렬은 배열을 절반으로 계속 나누어 더 이상 나눌 수 없을 때까지 반복
그런 다음, 정렬된 부분 배열들을 병합하여 최종적으로 정렬된 배열

재귀적 호출
각 부분 배열을 정렬하기 위해 재귀적으로 병합 정렬을 호출

병합 과정
정렬된 두 부분 배열을 병합할 때, 각 배열의 첫 번째 요소를 비교하여 작은 값을 결과 배열에 추가, 이 과정을 반복하여 최종적으로 정렬된 배열을 얻음

힙 정렬 (Heap Sort)

힙 자료구조
힙 정렬은 힙 자료구조를 기반함, 힙은 완전 이진 트리의 일종으로, 부모 노드가 자식 노드보다 항상 크거나 작은 특성을 갖음 (최대 힙 또는 최소 힙).

최대 힙 구성
먼저, 정렬되지 않은 배열을 최대 힙으로 구성
이 과정에서 부모 노드가 자식 노드보다 항상 크도록 힙 속성을 유지

정렬 과정
최대 힙의 루트 노드(가장 큰 값)를 힙의 마지막 요소와 교환하고, 힙 크기를 줄여서 다시 힙 속성을 유지. 이 과정을 반복하여 정렬된 배열을 얻음

🌍이차 시간 복잡도

동적 계획법, 넥센 문제 등등

동적 계획법
큰 문제를 여러 개의 작은 부분 문제로 나누어 해결하고, 각 부분 문제의 해를 저장하여 중복 계산을 피하는 알고리즘 설계 기법

동적 계획법의 활용
최단 경로 문제: 그래프에서 두 점 사이의 최단 거리를 구하는 문제에 사용
예를 들어, 구글 지도에서 길 찾기 기능와 같은 서비스에서 활용
배낭 문제(Knapsack Problem): 제한된 용량의 배낭에 최대한 많은 가치를 가진 물건들을 넣는 문제에 사용

문자열 유사도 계산
두 문자열의 유사도를 계산하는 문제에 사용

🌍삼차 시간 복잡도

알고리즘의 실행 시간이 입력 크기 (n)의 세제곱에 비례하여 증가하는 것

플로이드 워셜
모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구해야 하는 경우를 구하는 알고리즘

📌결론

알고리즘이 얼마나 빠르게 동작하는지 평가하기 위해 사용

🎯 예시

let array = [1,2,3,4,5] // 5개의 데이터(N = 5)
let summary = 0; // 합계를 지정할 변수

// 모든 데이터를 하나씩 확인하며 합계를 계산
for(let i = 0; i < array.length; i++){
  summary += array[i];
}

// 결과를 출력
console.log(summary)

수행시간은 데이터 개수 N에 비례할 것임을 예측 가능
O(N) : 선형 시간 복잡도 

let array = [3,5,1,2,4] // 5개의 데이터(N = 5)
let summary = 0; // 합계를 지정할 변수

// 모든 데이터를 하나씩 확인하며 합계를 계산(5의 n제곱)
for(let i = 0; i < array.length; i++){ // i가 한번 바뀔때마다
  for(let j= 0; j < array.length; j++){ // j가 다섯번씩 변경됨
    let temp = array[i] * array[j]
    console.log(temp)
}

// 결과를 출력 
console.log(summary)

모든 2중문이 시간 복잡도가 O(N²)은 아니니 소스코드가 내부적으로 호출하는 함수 고려
O(N²): 이차 시간 복잡도

💪알고리즘 설계 TIP

  • 일반적인 CPU 기반 개인 컴퓨터
  • JS기준 1억번의 연산은 1~5초
  • O(N³) 설계의 경우 , N이 5,000이 넘는다면 걸리는 시간은?
  • 코딩 테스트 시간 제한 : 1~5초
  • 명시 X : 5초

💪요구사항에 따른 적절한 알고리즘 설계

  • 시간제한(수행 시간 요구사항)
  • 시간 제한이 1초인 문제를 만났을 때, 일반적인 기준은 다음과 같다.
  • 𝑁의 범위가 500인 경우 : 시간 복잡도가 𝑂(N³) 설계
  • 𝑁의 범위가 2,000인 경우 : 시간 복잡도가 𝑂(N³) 설계
  • N의 범위가 2,000인 경우: 시간 복잡도가 𝑂(N²) 설계
  • 𝑁의 범위가 100,000인 경우: 시간 복잡도가 O(N log N) 설계
  • 𝑁의 범위가 10,000,000인 경우: 시간 복잡도가 O(N) 설계

범위를 미리 파악하고 역으로 어느 정도로 동작하는지 이해해서 푸는 것

profile
최유나

0개의 댓글