[Today I Learend 11] 1. 레드-블랙 트리

이번 주차에는 처음으로 C언어를 배우고 레드-블랙 트리를 배우는 시간이다. C언어 문법을 배우기 전에 레드-블랙 트리에 대해 알아보려고 한다.

1. 레드-블랙 트리의 특성

• 이진 검색 트리로서 각 노드당 한 비트의 추가 기억 공간을 가진다.
• 비트는 노드의 색깔을 나타내는데, 적색(Red)나 흑색(Black)이 될 수 있다.
• Root에서 Leaf까지의 경로에 나타나는 노드의 색깔을 제한함으로써 그러한 경로 중 어떠한 것도 다른 것보다 두 배 이상 길지 않음을 보장하게 된다.
• 근사적으로 균형을 이룬 트리가 된다.
• 각 노드의 필드 color, key, left, right, p

  ❗ 특성

  1. 모든 노드는 적색이거나 흑색이다.
  2. 루트는 흑색이다.
  3. 모든 리프(NIL)는 흑색이다.
  4. 노드가 적색이면 그 노드의 자식은 모두 흑색이다.
  5. 각 노드로부터 그 노드의 자손인 리프로 가는 경로들은 모두 같은 수의 흑색 노드를 포함한다.

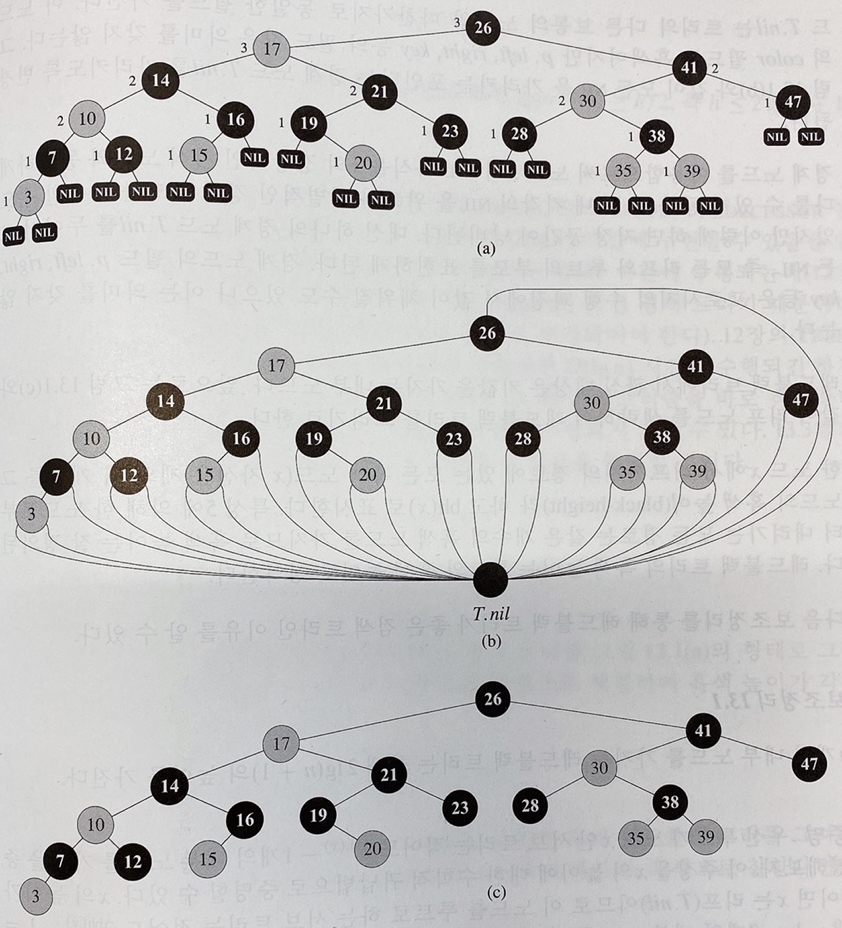
그림 1. 흑색 노드를 검정색, 적색 노드를 연한 회색으로 표시한 레드 블랙 트리이다.

❗그림 1 설명
(a) NIL로 표시된 모든 리프 노드는 흑색이다. NIL이 아닌 모든 노드는 그 노드의 흑색 높이를 함께 표시 했다. 단, NIL은 흑색 높이 0을 가진다.
(b) 각각의 NIL을 흑색인 하나의 경계노드 T.nil로 치환한 동일한 레드블랙 트리의 모습이다.
(c) 리프와 루트의 부모 노드를 모두 생략한 동일한 레드블랙 트리이다.

2. 정리

여기서 레드-블랙 트리가 좋은 검색 트리인 이유를 설명 하려고 한다.

• n 개의 내부 노드를 가지는 레드 블랙 트리는 최대 $2log_{2}(n+1)$의 높이를 가진다.
• 이진 트리는 최악의 경우 트리의 최대 높이가 n이 될 수 있다.

❗ 증명
참고: bh는 블랙 노드의 높이이다.
루트가 노드 x인 서브 트리는 적어도 $2^{bh(x)} - 1$개의 내부 노드를 가짐을 증명 하겠다.

1. 수학적 귀납법

• x의 높이가 0이면 x는 리프(T.nil)이므로 이 노드를 루트로 하는 서브 트리는 적어도 $2^{bh(x)} - 1 = 2^0 - 1 = 0$개의 내부 노드를 가진다.

2. 가정

• 노드 x가 양의 높이를 가지고 두 자식을 가지는 내부 노드라고 하자.
• 각 자식은 자신의 색깔이 적색 또는 흑색이냐에 따라 bh(x) 또는 bh(x) - 1의 높이를 가진다.
• x의 자식의 높이는 x의 높이보다 작으므로 귀납적 가정을 적용하여도 적어도 2^bh(x) - 1개의 내부 노드를 가진다고 결론 내릴 수 있다.

3. 결론

• x를 루트로 하는 서브 트리는 적어도 ($2^{bh(x)-1} - 1) + (2^{bh(x)-1} - 1) + 1 = 2^{bh(x)} - 1$개의 내부 노드를 가지므로 앞의 명제가 증명되었다.