1. 이진 탐색 핵심!!!
오늘은 이진 탐색의 핵심을 정리 해보려고 한다.
1. 정렬되어있는 배열에서 사용을 해야된다.
2. 시작점과 끝점을 지정할 때 정해야된다. (문제에 다 나와있다.)
2. 풀면서 어려웠던 백준 문제
- 공유기 설치(#2110)
문제
도현이의 집 N개가 수직선 위에 있다. 각각의 집의 좌표는 x1, ..., xN이고, 집 여러개가 같은 좌표를 가지는 일은 없다.
도현이는 언제 어디서나 와이파이를 즐기기 위해서 집에 공유기 C개를 설치하려고 한다. 최대한 많은 곳에서 와이파이를 사용하려고 하기 때문에, 한 집에는 공유기를 하나만 설치할 수 있고, 가장 인접한 두 공유기 사이의 거리를 가능한 크게 하여 설치하려고 한다.
C개의 공유기를 N개의 집에 적당히 설치해서, 가장 인접한 두 공유기 사이의 거리를 최대로 하는 프로그램을 작성하시오.입력
첫째 줄에 집의 개수 N (2 ≤ N ≤ 200,000)과 공유기의 개수 C (2 ≤ C ≤ N)이 하나 이상의 빈 칸을 사이에 두고 주어진다. 둘째 줄부터 N개의 줄에는 집의 좌표를 나타내는 xi (0 ≤ xi ≤ 1,000,000,000)가 한 줄에 하나씩 주어진다.
출력
첫째 줄에 가장 인접한 두 공유기 사이의 최대 거리를 출력한다.
가지고 있는 정보는 집의 개수, 공유기의 개수, 집의 좌표 였습니다. 이것만 보고 처음에는 접근 방법이 떠오르지 않아서 한참을 헤메인것 같습니다. 제가 문제에 접근 했던 방식을 한번 써보려고 합니다. 저는 위에 적어놓은 핵심 키워드를 생각하면서 접근해봤습니다.
- 정렬 되어 있는 배열!!! (이 키워드에서 생각할 수 있던게 지금 정렬을 할 수 있는 건 집의 좌표이다.)
- 시작점과 끝점!!! (여기서는 감이 확실하게 잡히지 않았지만 정렬되어 있는 집의 좌표의 첫번째와 마지막번째를 정하면 되겠다라는 생각을 해봤습니다.)
이런 생각을 가지고 코드를 한번 작성 해봤습니다.
from sys import stdin
input = stdin.readline
n, c = map(int, input().split()) # 집의 개수, 공유기의 개수
house_arr = [int(input()) for _ in range(n)] # 집의 좌표
house_arr.sort() # 집의 좌표 정렬
def bin_search():
start = 1 # 공유기를 설치할 수 있는 최소 거리
end = house_arr[len(house_arr) - 1] - house_arr[0] # 공유기를 설치할 수 있는 최대 거리
temp = 0
while start <= end: # 공유기를 설치할 수 있는 최소 거리와 최대 거리가 교차 한다면 종료
mid = (start + end) // 2 # 공유기 설치 거리
house = house_arr[0] # 공유기 설치한 집
cnt = 1 # 공유기 개수
for i in house_arr: # 공유기 설치
if i >= house + mid: # 공유기 설치한 집과 공유기 설치 거리를 더했을 때 집의 좌표가 크거나 같으면 설치 가능
cnt += 1 # 공유기 설치 완료
house = i # 마지막으로 공유기 설치한 집
if cnt >= c: # 설치한 공유기가 설치 해야될 공유기보다 크거나 같을 때
start = mid + 1
temp = mid # else로 빠져버리면 최적의 해가 아니기 때문에 전에 mid값을 저장
else: # 설치한 공유기가 설치 해야될 공유기보다 작을 때
end = mid - 1
return temp
print(bin_search())- 사냥꾼(#8893)
문제
KOI 사냥터에는 N 마리의 동물들이 각각 특정한 위치에 살고 있다. 사냥터에 온 사냥꾼은 일직선 상에 위치한 M 개의 사대(총을 쏘는 장소)에서만 사격이 가능하다. 편의상, 일직선을 x-축이라 가정하고, 사대의 위치 x1, x2, ..., xM은 x-좌표 값이라고 하자. 각 동물이 사는 위치는 (a1, b1), (a2, b2), ..., (aN, bN)과 같이 x,y-좌표 값으로 표시하자. 동물의 위치를 나타내는 모든 좌표 값은 양의 정수이다.
사냥꾼이 가지고 있는 총의 사정거리가 L이라고 하면, 사냥꾼은 한 사대에서 거리가 L 보다 작거나 같은 위치의 동물들을 잡을 수 있다고 한다. 단, 사대의 위치 xi와 동물의 위치 (aj, bj) 간의 거리는 |xi-aj| + bj로 계산한다.
예를 들어, 아래의 그림과 같은 사냥터를 생각해 보자. (사대는 작은 사각형으로, 동물의 위치는 작은 원으로 표시되어 있다.) 사정거리 L이 4라고 하면, 점선으로 표시된 영역은 왼쪽에서 세 번째 사대에서 사냥이 가능한 영역이다.
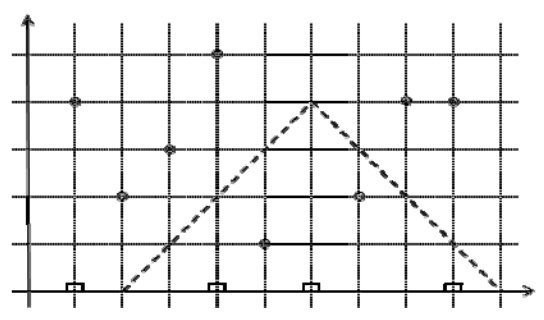
사대의 위치와 동물들의 위치가 주어졌을 때, 잡을 수 있는 동물의 수를 출력하는 프로그램을 작성하시오.입력
첫째 줄에 집의 개수 N (2 ≤ N ≤ 200,000)과 공유기의 개수 C (2 ≤ C ≤ N)이 하나 이상의 빈 칸을 사이에 두고 주어진다. 둘째 줄부터 N개의 줄에는 집의 좌표를 나타내는 xi (0 ≤ xi ≤ 1,000,000,000)가 한 줄에 하나씩 주어진다.
출력
첫째 줄에 가장 인접한 두 공유기 사이의 최대 거리를 출력한다.
가질 수 있는 정보는 사대 수, 동물 수, 사정거리, 사대 위치 x좌표, 동물 위치 [x, y] 좌표이다. 제가 접근 했던 방식은 이중에서 정렬하기 적합한 것부터 찾아보고 위에 적어놓은 핵심 키워드를 생각하면서 접근해봤습니다.
- 정렬 되어 있는 배열!!! (이 키워드에서 생각할 수 있던게 사대 위치 x좌표가 정렬하기 편하다고 생각했습니다.)
- 시작점과 끝점!!! (여기서는 정렬된 사대 위치 x좌표에서 배열한의 최솟값과 최대값보다 인덱스 값으로 접근해야 사냥할 수 있는지 없는지에 대해 판단할 수 있다고 생각했습니다.)
from sys import stdin
input = stdin.readline
M, N, L = map(int, input().split()) # 사대 수, 동물 수, 사정거리
M_x = list(map(int, input().split())) # 사대 위치 x좌표
A_x_y = [list(map(int, input().split())) for _ in range(N)] # 동물 위치 [x,y] 좌표
M_x.sort() # 사대 위치 정렬
cnt = 0 # 사냥한 동물 수
for i in A_x_y: # 동물의 좌표를 하나 씩 꺼냄
start = 0 # 시작점 사대 위치 처음 인덱스
end = M - 1 # 끝점 사대 위치 마지막 인덱스
while start <= end: # 이진 탐색 부분
mid = (start + end) // 2 # 사대 위치 x좌표 배열의 가운데 인덱스
if abs(i[0] - M_x[mid]) + i[1] <= L: # 사냥 할 수 있다면 아무나 사냥해도 됨
cnt += 1
break
if i[0] > M_x[mid]: # 만약에 사냥할 수 없는데 동물의 x좌표가 사대 위치보다 크다면 시작 인덱스를 mid + 1로 이동
start = mid + 1
else: # 만약에 사냥할 수 없는데 동물의 x좌표가 사대위치보다 작다면 끝 인덱스를 mid + 1로 이동
end = mid - 1
print(cnt)3. 느낌점
❗이번에 이진 탐색 문제를 풀면서 위에 적어 놓은 핵심 키워드가 중요하다고 느꼈습니다. 또한, 모든 이진 탐색 문제들이 이럴지는 모르지만 간단한 틀이 있습니다.
while 시작점 <= 끝점: # 배열을 모두 탐색할 때 필요한 조건
mid = (시작점 + 끝점) # 가운데 값 구하기
if 특정한 조건: # 만약에 값을 찾았을 때 빠져나오고 싶으면
break
if 찾아야하는 값 > 현재 위치의 값: # 만약 현재 위치의 값이 찾아야하는 값보다 작다면(찾아야 될 값이 오른쪽에 있다는 뜻)
시작점 = mid + 1 # 시작점을 가운데 + 1 값으로 변경
else: # 만약 현재 위치의 값이 찾아야하는 값보다 크다면(찾아야 될 값이 왼쪽에 있다는 뜻)
끝점 = mid - 1 # 끝 점을 가운데 - 1 값으로 변경

