
📚 문제
https://www.acmicpc.net/problem/14500
📖 풀이
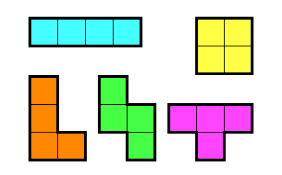
가장 합이 최대가 되는 테트로미노 모양을 찾는 것이다.
보라색 모형 빼고 나머지는 스택을 활용하여 구할 수 있다. 무조건 연결되는 부분으로 붙어야 한다.
따라서 나머지 4가지 도형은 DFS로 탐색하여 구하고, 보라색은 따로 구해준다.
보라색을 제외한 4가지 도형 탐색 방법
현재 점 기준 DFS로 4칸 움직이는 모든 경우를 구하고, 최댓값을 구한다.
BFS를 사용할 수 없는 이유는 스택을 활용해서 하나씩 붙여줘야하기 때문에 DFS를 사용한다.
DFS를 사용할 때 중요한 포인트는, 현재 좌표는 방문표시를 해 확인한 칸은 다시 확인하지 않도록 한다. 그리고 확인했으면 다시 방문표시를 지워야 한다.
탑다운 방식을 사용해서 해결한다. 네 방향으로 탐색하면서 네 방향 중 가장 큰 값을 리턴하는 방식으로 접근한다. 그러면 길이가 4인 합이 가장 큰 값을 리턴하게 된다. 방문표시를 앞 뒤로 해줘야하니 신경써야 한다!
보라색 탐색 방법
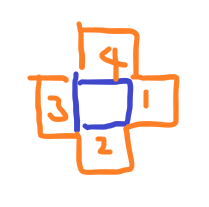
현재 좌표 기준 네 방향을 탐색한다.
네 방향의 값을 리스트에 담아 3개 이상인 경우만 합을 리턴한다. 아닌 경우는 0을 리턴해 최댓값 비교할 때 갱신할 수 없게 만든다.
네 개의 값이면 정렬시켜 크기가 큰 3개의 값의 합을 리턴한다. 거기다가 가운데 값인 현재 좌표 값을 더해서 비교한다.
📒 코드
def in_range(x, y): # 범위를 만족시키는지 확인할 함수
return 0 <= x < n and 0 <= y < m
def dfs(cur, x, y, total): # 연결된 4개의 테트로미노 구하기
if cur == 3: # 4개 연결된 경우
return total
visited[x][y] = 1 # 연결한 좌표를 다시 탐색하지 않도록 방문표시
ret = 0 # 탑다운 방식으로 해결하기 위해 리턴값을 정의한다.
for i in range(4): # 네 방향 탐색
nx = x + dx[i]
ny = y + dy[i]
if in_range(nx, ny) and not visited[nx][ny]:
ret = max(ret, dfs(cur + 1, nx, ny, total + arr[nx][ny])) # 네 방향 중 최대값을 리턴한다.
visited[x][y] = 0 # 마지막에 방문표시를 다시 지워줘야 한다.
return ret
def purple(x, y): # 보라색 테트로미노를 확인할 함수('ㅗ' 모양)
nums = [] # 현재 좌표 기준 네 방향으로 존재하는 값들을 다 담아줄 리스트
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if in_range(nx, ny): # 범위를 만족한 경우 담아준다.
nums.append(arr[nx][ny])
if len(nums) >= 3: # 길이가 3 이상인 경우만 합해서 리턴
nums.sort(reverse=True) # 크기가 큰 3개를 더해서 리턴
return sum(nums[0:3])
else: # 길이가 3보다 작으면 0을 리턴해서 최댓값 비교해도 바뀌지 않도록 한다.
return 0
n, m = map(int, input().split())
arr = [list(map(int, input().split())) for _ in range(n)]
visited = [[0] * m for _ in range(n)]
dx = [0, 1, 0, -1]
dy = [1, 0, -1, 0]
result = 0
for i in range(n):
for j in range(m):
result = max(result, dfs(0, i, j, arr[i][j]), purple(i, j) + arr[i][j])
print(result)🔍 결과

