
📚 문제 : 선분 교차 2
📖 풀이
나올 수 있는 길이가 2000000이라 이차원 배열로 방문표시하면 메모리 초과가 발생한다.
선분의 교차점으로 해결하려고 하면 나눗셈인 실수 계산이 들어가 출력된 값에 에러가 발생한다.
기하 알고리즘을 공부할 때 필수로 알아야 하는 CCW로 해결해야 한다.
CCW 란?
예전 삼각형의 넓이를 구하던 사선 공식과 동일하다.
세 점을 이용하여 각도를 구한다.
p1 = (x1, x1), p2 = (x2, y2), p3 = (x3, y3), p4 = (x4, y4)라고 하면
CCW(p1,p2,p3)는 아래와 같이 구할 수 있다.
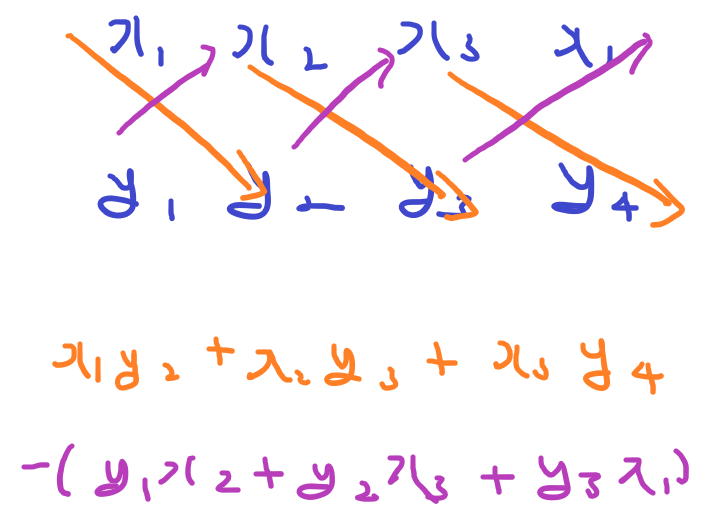
위 처럼 구하면 p1을 축으로 p1과 p2의 벡터와 p1과 p3의 벡터의 회전 방향이 시계방향인지 반시계방향인지에 따라 값이 나온다. 같은 라인에 있으면 0이다.
CCW의 뜻은 Counter Clock Wise로 반시계방향일 때 양수가 나온다고 외우면 쉽다.
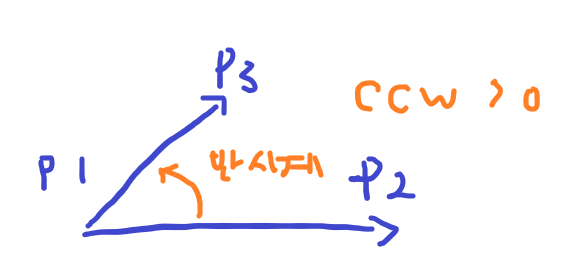
-
직선에서 겹치는지 확인 할 때에는 한 선분에서 다른 선분의 양 끝점으로 CCW를 구해 두 CCW의 값을 곱하여 교차하는지 판단한다.
CCW(p1, p2, p3) * CCW(p1, p2, p4) < 0 -
직선 같은 경우는 한 선분을 기준으로 삼아 CCW의 곱을 구하면 되지만, 선분인 경우는 두 선분 각각 CCW의 곱을 구해보아야 한다.
(CCW(p1, p2, p3) * CCW(p1, p2, p4) < 0) and (CCW(p3, p4, p1) * CCW(p3, p4, p2) < 0)
이유는 직선으로 만나지만 선분으로는 안 만나는 경우가 있다.
- CCW의 곱이 하나는 0보다 작지만, 하나는 0보다 크게 된다.
- 따라서 선분으로 만나는지 구하려면 양 선분 둘 다 CCW의 곱을 구해봐야 한다.
-
두 선분의 교차점이 p1, p2, p3, p4 위에 있거나, 하나의 직선 위에 네 점이 놓이는 경우
(CCW(p1, p2, p3) * CCW(p1, p2, p3) == 0) and (CCW(p3, p4, p1) * CCW(p3, p4, p2) == 0)
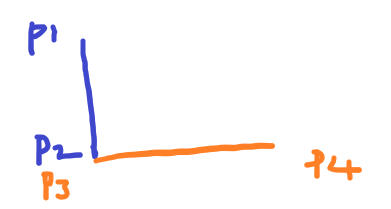
따라서 두 선분에서 CCW 곱이 다 0보다 작거나 같게된다면 그 때는 교차하는 것이다.
이 때 주의할 점은 두 선분에서의 CCW의 곱이 다 0이면, 이 때에는 겹치는 지 확인해주어야 한다.
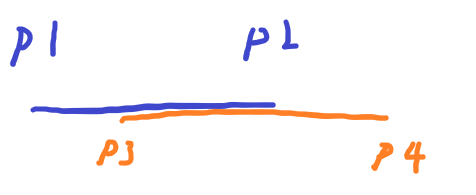
p1 < p2 이고 p3 < p4라고 하면, p3 <= p2 and p1 <= p4를 만족하면 두 직선은 교차한다.
만족하지 않는 경우는 아래와 같다.
📒 코드
def ccw(p1, p2, p3):
return p1[0] * p2[1] + p2[0] * p3[1] + p3[0] * p1[1] - \
(p1[1] * p2[0] + p2[1] * p3[0] + p3[1] * p1[0])
x1, y1, x2, y2 = map(int, input().split())
x3, y3, x4, y4 = map(int, input().split())
p1, p2 = [x1, y1], [x2, y2]
p3, p4 = [x3, y3], [x4, y4]
p12 = ccw(p1, p2, p3) * ccw(p1, p2, p4) # p1, p2 선분으로 p3과 p4에 대한 ccw의 곱
p34 = ccw(p3, p4, p1) * ccw(p3, p4, p2) # p3, p4 선분으로 p1과 p2에 대한 ccw의 곱
if p12 <= 0 and p34 <= 0: # 두 선분이 교차하는 경우(한 직선 위에 있을 때 생각!)
if p12 == 0 and p34 == 0: # 두 선분이 같은 라인에 있을 때
p1, p2 = min(p1, p2), max(p1, p2)
p3, p4 = min(p3, p4), max(p3, p4)
if p3 <= p2 and p1 <= p4: # 두 선분이 만나는 경우
print(1)
exit()
else:
print(1)
exit()
print(0) # 나머지는 교차하지 않는다.🔍 결과

