
📚 문제
https://www.acmicpc.net/problem/2436
최대 공약수와 최소 공배수가 주어졌을 때, 두 개의 자연수를 구하는 문제이다.
최대 공약수 N, 최소 공배수 M, 두 개의 자연수는 A , B(A<=B) 라고 하자.
최대 공약수와 최소 공배수의 관계를 생각한다.
최대 공약수와 최소 공배수의 곱은 두 자연수의 곱이다
A * B = N * M두 자연수는 최대 공약수의 배수이다.
A = N * a,
B = N * b
N을 알고 있으니 a, b만 구하면 된다.
위 두 식을 조합해보면 a * b = M // N 이다.
약수 구하기
M // N값의 약수를 구한다. 약수를 구해 두 수를 튜플로 리스트에 담는다.서로소 구하기
그리고 그 약수들 중 서로소를 찾아야 하니 유클리드 호제법을 사용해 최소 공배수가 1인 두 수만 새로운 리스트에 담는다.
최소값 구하기
서로소 리스트를 순회하며 합을 구해 최소값을 찾는다.
위 방법으로 작성해서 제출해보니!
🔍 1차 제출 결과

96% 달성할 쯤 런타임 에러가 발생한다. 두 수가 같을 때 처리를 안해줘서 그런 것 같아 조건문을 추가한다.
두 개가 같은 경우를 처리하기 위해 같을 때 두 수를 그대로 출력하게 한다.
📒 코드
N, M = map(int, input().split()) # N 최대공약수, M 최소공배수
if N == M: # N, M이 같을 때 입력 그대로 출력한다.
print(N, N)
else:
constant = M//N # 최대 공배수에서 최소 공배수를 나눈다.
div_num = constant # 약수 구하면서 값이 바뀌니 다른 변수에 저장
div_lst = [] # 약수의 짝을 튜플로 담을 리스트
for i in range(1, div_num):
if i * i > div_num: # 제곱근 이상의 약수는 구할 필요 없다.
break
if div_num % i == 0: # 약수 구하기, 약수의 짝을 항상 생각한다.
if i * i == div_num: # 제곱수일 때 처리해준다.
div_lst.append((i,i))
else: div_lst.append((i,constant//i)) # i에 더 작은 값이 들어간다.
each_other_lst = [] # 서로소 약수 짝을 튜플로 담을 리스트
for i in range(len(div_lst)): # 유클리드 호제법으로 서로소인지 구하기
a, b = div_lst[i] # 약수를 담은 리스트에서 tuple 하나씩 가져온다.
while a % b != 0: # 두 수의 최대 공약수를 구해준다.
a, b = b, a % b # a가 b로 나누어 떨어지는 순간 출력되는 b가 최대 공약수이다.
if b == 1: # 최대 공약수가 1일 때가 서로소이다.
each_other_lst.append(div_lst[i])
a = each_other_lst[0][0]
b = each_other_lst[0][1]
min = a + b # a + b값을 서로소 리스트의index 0 값으로 초기화
for x, y in each_other_lst:
if min > x + y: # 합이 더 작을 때 a, b에 담아준다.
min = x + y
a = x
b = y
print(a*N, b*N) # A, B는 a*N, b*N이니 다시 곱해서 출력한다.🔍 결과

약수 구할 때 제곱근 활용 및 제곱 수일 때 조심하는 것과 유클리드 호제법으로 최소 공배수를 구해 서로소를 찾는 방법이 필요하다.
두 수가 같을 때 처리해주지 않아 런타임 에러가 발생했으니 좀 더 꼼꼼히 문제를 확인하자!
좀 더 나은 해답 발견!
약수의 짝의 합이 제곱근에 가까워질수록 작아진다는 것을 활용한다.
n의 약수 중 하나를 x라고 하자.
그러면 다른 약수는 x/n이다.
우리는 x + x/n의 최솟값을 구한다.
x+x/n을 미분하면 1-n/(x^2) 이다.
따라서 x가 [0,x의 제곱근] 구간에서는 항상 감소한다.
그러므로 제곱근에 가까워진 x의 짝의 합이 가장 작다.
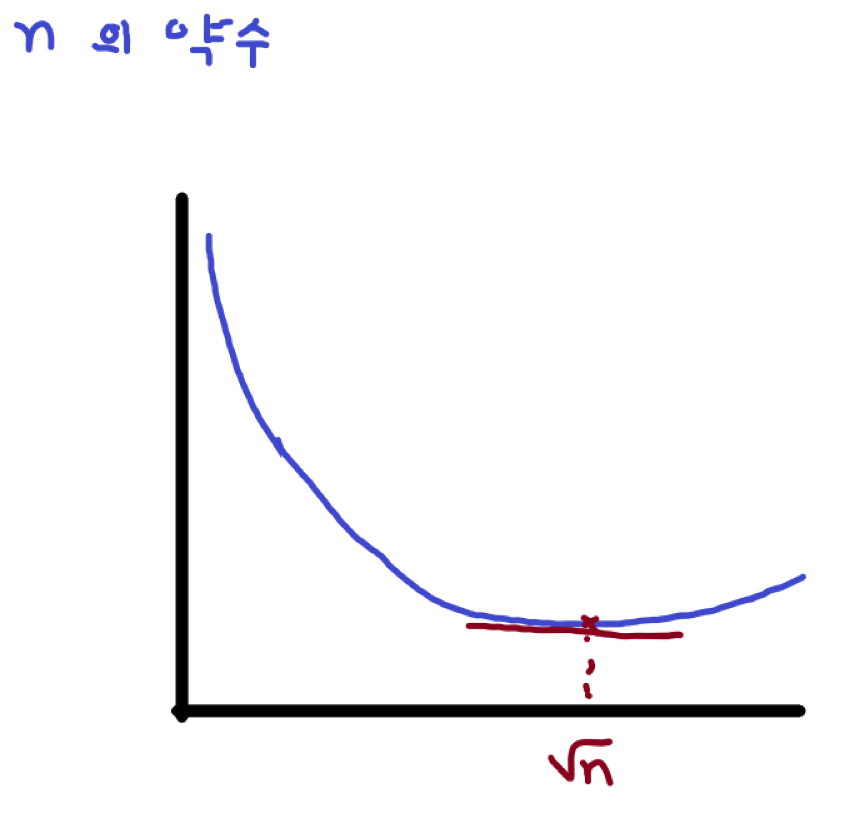
그러면 a, b를 뽑아 약수인지 확인하고 서로소인지까지 확인한 후 값을 고르면 된다. 어차피 제곱근이하가 될 때까지 a, b를 구한 후 for 문이 끝나기 때문에 리스트에 넣어줄 필요가 없다. 두 수가 같을 때도 리스트에 담지 않으니 신경쓰지 않아도 된다.
📒 코드
N, M = map(int, input().split())
constant = M//N
div_num = constant
for i in range(1, div_num+1):
if i * i > div_num:
break
if div_num % i == 0:
x = i
y = constant//i
while x % y != 0:
x, y = y, x % y
if y == 1:
a = i
b = constant//i
print(a*N, b*N)🔍 결과

x+n/x 같이 역수의 합은 n(양수)의 제곱근에서 가장 최솟값을 갖는다는 걸 기억하자!

와... 마크다운 마스터 하셨네요 굿
그래서 선생님 미분이 뭔가요?