
📚 문제 : 과외맨
📖 풀이
구현 문제이다.
그래프 문제로 최단거리를 구해야 하니 BFS로 구한다.
타일로 구성되어있으니 n x (n * 2) 의 2차원 배열을 구현해 담아준다.
짝수줄의 양 끝은 0을 담아 주변 타일과 연결되지 않도록 한다.
처음에는 큐에 타일 조각 2개를 묶어서 담지 않고 하나씩 담아 BFS로 푸려고 했다. 그렇게하니 시간초과가 발생해 큐에 타일 조각 2개를 묶어서 담아 시간 초과를 해결했다.
-
먼저 직사각형이 아닌 타일들을 어떻게 2차원으로 담아줄 지 생각했다.
짝수 행일 때와 홀수 행일 때가 다르므로 그 때를 구분해주어 담아준다.
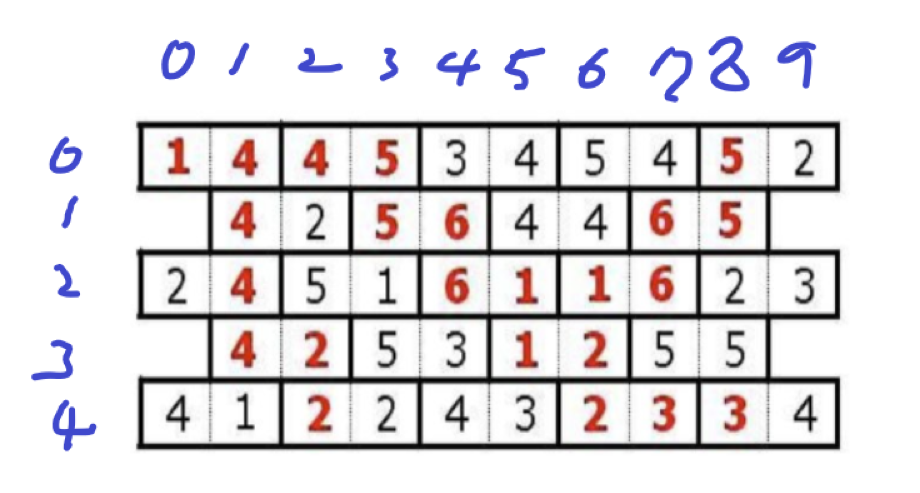
위 그림에서 보면 x는 [0 ~ n-1], y는 [0 ~ n*2 - 1]의 범위로 초기화 한다.
그리고 짝수 행일 때와 홀수 행일 때를 구분하여 담아준다.
코드로 보면 다음과 같다.
graph = [[0] * n * 2 for _ in range(n)]
# 타일을 담아주는 방법, 짝수 행일 때와 홀수 행일 때를 구분해서 2차원 배열에 담는다.
for i in range(n):
for j in range(n - i % 2):
t1, t2 = map(int, input().split())
graph[i][2 * j + i % 2] = t1
graph[i][2 * j + 1 + i % 2] = t2짝수 행은 [0 ~ n - 1]이고, 홀수 행은 범위를 [1 ~ n - 2]로 좁혀준다.
-
bfs로 타일을 하나씩 이동해나간다.
bfs에 하나의 타일에 연결된 두 조각을 담는다.
그러면 [[x1, y1], [x1, y1 + 1]]와 같은 형태로 큐에 넣는다.
큐에서 오른쪽 조각과 왼쪽 조각으로 나누어 주변 타일들을 확인한다.
오른쪽 조각부터 그림을 보면 아래와 같다.(파란색이 현재 타일이다.)
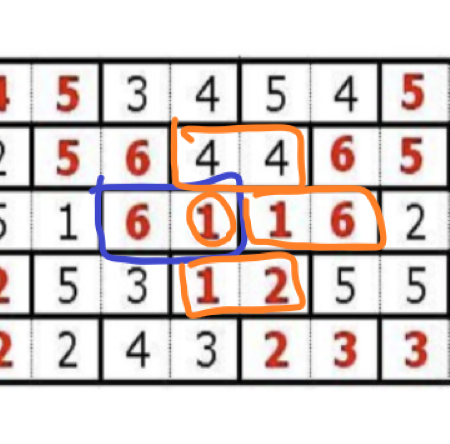
오른쪽, 위, 아래 타일들이 인접한 타일들이다. 이 때 인접한 타일 조각들의 왼쪽 부분이랑만 닿아있는 걸 확인할 수 있다. 따라서 인접한 조각의 오른쪽 조각을 함께 큐에 담아준다.
왼쪽 타일도 마찬가지이다. 인접한 조각이 오른쪽 부분에 닿아 있으니 왼쪽 조각을 함께 큐에 넣어주면 된다.
똑같은 타일을 또 방문하지 않기 위해서는 어떻게 해야 할까?
-
확인했던 타일들을 다시 확인하지 않도록 visited 배열을 설정한다.
visited 배열에 타일을 지난 순서를 적어준다. 이미 적은 횟수로 그 타일에 갔으면 확인하지 않아도 되기 때문이다. 이동할 타일이 현재 타일의 visited 값보다 2이상 큰 수 일 때만 옮겨간다.
1 크기만 해도 똑같은 순서에다가 이미 확인했던 값이니 또 확인할 필요가 없다.
더 큰 쪽으로만 움직여야 하므로 처음에 INF 값으로 나올 수 없는 가장 큰 수로 초기화한다.
타일을 방문 처리할 때 두 조각을 한꺼번에 처리해준다.
-
마지막 줄의 마지막 타일로 이동할 수 없는 경우가 존재할 수 있다. 이 경우에는 번호가 가장 큰 타일로 이동하면 된다.
맨 마지막 타일에 도달하지 못할 수 있으니 타일을 뒤부터 확인하며 INF가 아닌 다른 값이 들어갔는지 확인한다. INF가 아니면 도달했을 때이니 그 때의 숫자를 출력하면 된다.
# 도착지 찾기 def find_destination(): for i in range(n)[::-1]: for j in range(2 * n)[::-1]: if visited[i][j] != INF: # 가장 큰 타일까지 방문 횟수와 도착지 타일 번호 리턴 return visited[i][j], find_tile_num(i, j)
-
우리는 타일이 진행된 경로도 출력해야 한다. 따라서 역추적을 해야한다.
역추적을 하기 위해 타일 번호에 맞춰 이전의 타일 값을 저장해준다. 그러면 우리는 최종적으로 도달한 마지막 타일부터 역으로 어느 경로로 왔는지 확인할 수 있다. 시작점까지 배열에 담아 출력해준다.
# 도착점에서 출발지까지 역추적 def trace_back(num): ans = [num] while num: num = tiles[num] if not num: break ans = [num] + ans return ans
-
타일 번호를 알기 위한 함수를 하나 만들어야 위 과정을 수월하게 해결할 수 있다. 좌표의 값으로 타일의 번호를 찾는 함수를 만든다.
# 타일의 번호 찾기 def find_tile_num(x, y): # 행 : 짝수 줄 개수 * n + 홀수 줄 개수 * (n - 1) cnt_x = (x // 2 + x % 2) * n + (x // 2) * (n - 1) # 열 : 짝수 열일 때와 홀수 열일 때 차이 : 짝수 열이면 나머지도 더해준다. y += 1 cnt_y = y // 2 + (y % 2 if x % 2 == 0 else 0) return cnt_x + cnt_y
함정이 많아 모듈화를 깔끔하게 해야 실수 없이 해결할 수 있다.
📒 코드
import sys
from collections import deque
input = sys.stdin.readline
def in_range(x, y):
return 0 <= x < n and 0 <= y < 2 * n
def bfs():
que = deque()
# 시작점
visited[0][0] = 1
visited[0][1] = 1
que.append([[0, 0], [0, 1]]) # 큐에 타일을 담는다.(2조각이 한 쌍)
while que:
tile_left, tile_right = que.popleft()
for i in range(4):
x, y = tile_right # 오른쪽 타일부터 확인
nx = x + dx[i]
ny = y + dy[i]
if i == 2: # 왼쪽은 같은 타일이므로 생략
continue
if not in_range(nx, ny): # 범위 확인
continue
# 다음 조각의 방문 순서가 더 커야 한다.
if visited[nx][ny] > visited[x][y] + 1:
if graph[nx][ny] == graph[x][y]: # 인접한 두 값이 같은지 확인
que.append([[nx, ny], [nx, ny + 1]])
# 다른 타일로 이동했으니 방문 횟수를 + 1
visited[nx][ny] = visited[x][y] + 1
visited[nx][ny + 1] = visited[x][y] + 1
# 이동하면 이전 타일 값을 저장
tiles[find_tile_num(nx, ny)] = find_tile_num(x, y)
for i in range(4):
x, y = tile_left # 왼쪽 타일 확인
nx = x + dx[i]
ny = y + dy[i]
if i == 0: # 오른쪽은 같은 타일이므로 생략
continue
if not in_range(nx, ny): # 범위 확인
continue
# 다음 조각의 방문 순서가 더 커야 한다.
if visited[nx][ny] > visited[x][y] + 1:
# 다른 타일로 이동한 경우
if graph[nx][ny] == graph[x][y]: # 인접한 두 값이 같은지 확인
que.append([[nx, ny - 1], [nx, ny]])
# 다른 타일로 이동했으니 방문 횟수를 + 1
visited[nx][ny] = visited[x][y] + 1
visited[nx][ny - 1] = visited[x][y] + 1
# 이동하면 이전 타일 값을 저장
tiles[find_tile_num(nx, ny)] = find_tile_num(x, y)
cnt, tile_num = find_destination() # 이동 횟수와 도착지의 타일 번호
return cnt, trace_back(tile_num) # 이동 횟수와 경로 리턴
# 타일의 번호 찾기
def find_tile_num(x, y):
# 행 : 짝수 줄 개수 * n + 홀수 줄 개수 * (n - 1)
cnt_x = (x // 2 + x % 2) * n + (x // 2) * (n - 1)
# 열 : 짝수 열일 때와 홀수 열일 때 차이 : 짝수 열이면 나머지도 더해준다.
y += 1
cnt_y = y // 2 + (y % 2 if x % 2 == 0 else 0)
return cnt_x + cnt_y
# 도착지 찾기
def find_destination():
for i in range(n)[::-1]:
for j in range(2 * n)[::-1]:
if visited[i][j] != INF:
# 가장 큰 타일까지 방문 횟수와 도착지 타일 번호 리턴
return visited[i][j], find_tile_num(i, j)
# 도착점에서 출발지까지 역추적
def trace_back(num):
ans = [num]
while num:
num = tiles[num]
if not num:
break
ans = [num] + ans
return ans
n = int(input())
INF = n * 2 * n # 나올 수 없는 최대 값
dx, dy = [0, 1, 0, -1], [1, 0, -1, 0] # 우 하 좌 상
graph = [[0] * n * 2 for _ in range(n)]
# 타일을 담아주는 방법, 짝수 행일 때와 홀수 행일 때를 구분해서 2차원 배열에 담는다.
for i in range(n):
for j in range(n - i % 2):
t1, t2 = map(int, input().split())
graph[i][2 * j + i % 2] = t1
graph[i][2 * j + 1 + i % 2] = t2
# 방문 순서 담기
visited = [[INF] * n * 2 for _ in range(n)]
tiles = [0 for _ in range(n * n + 1)] # 이전 타일을 저장
cnt, result = bfs()
print(cnt)
print(*result)
🔍 결과

