기수정렬

버블, 선택, 삽입 알고리즘과 합병 퀵 알고리즘 지금까지 확인해본 정렬 알고리즘은 "비교"를 기본으로 하는 알고리즘입니다. 그래서 비교정렬이라고도 부릅니다.

비교정렬을 기본적으로 한번에 비교할 수 있는 숫자의 개수가 정해져있기 때문에 수학적으로 시간복잡도의 한계가 있다고 합니다. (위키피디아 참조)

그렇다면 비교알고리즘보다 좋은 성능의 알고리즘이 있을까요?

답은 yes 그러다 특정 상황에서만 해당합니다.
데이터의 특별한 속성을 사용합니다.

그중 하나가 기수 정렬(radix sort) 입니다.
이는 비교를 수행하지 않습니다. 그대신 숫자크기에 대한 정보를 자릿수로 인코딩 한다는 사실을 이용합니다. (10진수 기준으로 한자리당 올수 있는 숫자는 0~9가 됩니다)

기수정렬 helper 메소드

1. 자릿수 알아내기 함수
   getDigit(num,place) - 각 숫자와 자릿수를 반환해줍니다.

function getDigit(num, i) {
  return Math.floor(Math.abs(num) / Math.pow(10, i)) % 10;
}




getDigit(12345, 0); // 5
getDigit(12345, 2); // 3
getDigit(12345, 4); // 1
// num이라는 숫자의 0번위치(1의자릿수)는 5입니다
// num이라는 숫자의 2번위치(100의자릿수)는 3입니다
// num이라는 숫자의 5번위치(100000의자릿수)는 0입니다
// 012345는 12345와 같이 해석할 수 있습니다.  

2. 숫자가 몇의 자리수 숫자인지 알아내기
   digitCount(num) - return num의 최대 자리수

function digitCount(num) {
  if (num === 0) return 1;
  return Math.floor(Math.log10(Math.abs(num))) + 1;
}


digitCount(1); // 1 (1의 자리수)
digitCount(15); // 2 (10의 자리수)
digitCount(112); // 3 (100의 자리수)

3. 받은 숫자들 중에 가장 자릿수가 큰수는 어떤 것인지 판단하기
   mostDigits(nums) - return 제일 자릿수가 큰수의 최대 자릿수
   digitCount를 사용해서 구현합시다. 이를 위해 만든 함수니까요

function digitCount(num) {
  if (num === 0) return 1;
  return Math.floor(Math.log10(Math.abs(num))) + 1;
}

function mostDigits(nums) {
  let maxDigits = 0;
  for (let i = 0; i < nums.length; i++) {
    maxDigits = Math.max(maxDigits, digitCount(nums[i]));
  }
  return maxDigits;
}


mostDigits([1241,522,23,3]); // 4 (가장 큰수 1241은 최대 자릿수가 4입니다)
mostDigits([14441,52,213,28]); // 5 (14441 의 최대 자릿수)
mostDigits([41,2,3,1]); // 2 (41의 최대 자릿수)

기수정렬 구현 및 빅오

의사코드

1. 수 목록을 받는 함수를 정의합니다.
2. 가장 큰 수가 몇자리인지 알아 냅니다. mostDigits 을 사용하면 되겠죠
3. 0부터 가장 큰자릿수 까지 루프를 돌려줍니다.

• 반복 진행할 때 마다 각 자리수에 버킷을 만듭니다 (버킷은 빈 배열입니다)
• 각 숫자들을 kth 자릿수에 따라 버켓에 넣어줍니다.
  (kth 자릿수란 루프 k가 무엇이든 0에서 시작해서 각 수를 올바른 버킷에 저장하는 것 입니다)

4. 기존 배열을 버킷의 값으로 교체합니다.
5. 배열을 반환합니다.

코드 구현

function getDigit(num, i) {
  return Math.floor(Math.abs(num) / Math.pow(10, i)) % 10;
}

function digitCount(num) {
  if (num === 0) return 1;
  return Math.floor(Math.log10(Math.abs(num))) + 1;
}

function mostDigits(nums) {
  let maxDigits = 0;
  for (let i = 0; i < nums.length; i++) {
    maxDigits = Math.max(maxDigits, digitCount(nums[i]));
  }
  return maxDigits;
}

function radixSort(nums){
    let maxDigitCount = mostDigits(nums);
    for(let k = 0; k < maxDigitCount; k++){
        let digitBuckets = Array.from({length: 10}, () => []);
        for(let i = 0; i < nums.length; i++){
            let digit = getDigit(nums[i],k);
            digitBuckets[digit].push(nums[i]);
        }
        nums = [].concat(...digitBuckets);
    }
    return nums;
}

radixSort([23,345,5467,12,2345,9852])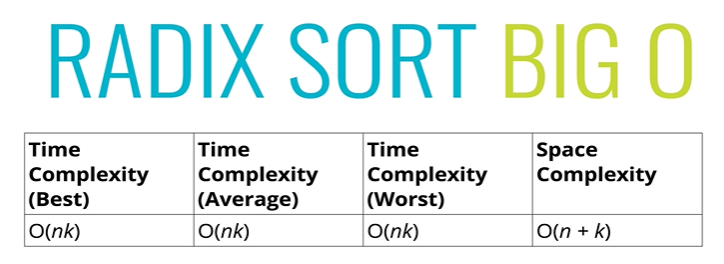

n는 정수의 수 , k는 자릿수의 최대치 입니다.

기수정렬의 효율성에 대해서 여러 의견이 있습니다... 복잡하기에 위키피디아에 맡기겠습니다. 읽어도 이해가 안갈수도있어요