문제 해결 패턴
문제 해결 패턴 소개
문제를 풀 때 사용되는 일반적인 패턴에 대해서 알아보겠습니다.
이는 여러 문제에 적용시킬 수 있습니다. 하지만 모든 것을 커버해주지는 않습니다.
- Frequency counter
- Multiple pointers
- sliding window
- divide and conquer
- dynamic programming
- greedty algorithms
- backtracking
- many more
빈도수 세기 패턴
주요 개념 : 자바스크립트의 객체를 사용해서 다양한 값과 빈도를 수집하는 것
예시 문제 : 2개의 배열을 허용하는 same이라는 함수를 작성하라
배열의 모든 값이 두 번째 배열에 해당하는 값을 가지면 참을 반환해야한다.
따라서 첫 번째 배열에는 여러 값이 있는데. 두 번째 배열의 값이 정확히 동일하지만 제곱되어 있는지 알고자 합니다. 하지만 순서는 상관 없으니 동일할 필요는 없고 그저 제곱만 하면 됩니다. 섞일 수 있지만 값의 빈도는 동일해야합니다.
same([1,2,3],[4,1,9]) // true
same([1,2,3],[1,9]) // false
same([1,2,3],[4,4,1]) // false (must be same frequency)해결책 1
function same(arr1, arr2){
if(arr1.length !== arr2.length){
return false;
}
for(let i = 0; i < arr1.length; i++){
let correctIndex = arr2.indexOf(arr1[i] ** 2)
if(correctIndex === -1) {
return false;
}
console.log(arr2);
arr2.splice(correctIndex,1)
}
return true;
}
same([1,2,3,2], [9,1,4,4])이중 for문이 사용되었습니다. O(N^2)의 시간복잡도를 가지겠군요.
원리는 첫 배열의 숫자 하나를 제곱하고 두번째 배열에 존재하는 지 확인합니다. 존재하면 해당 숫자를 지워주고 존재하지 않으면 바로 false를 반환 합니다. 이렇게 첫 배열의 모든 숫자를 두번째 배열과 비교합니다.
리팩터링 코드
function same(arr1, arr2){
if(arr1.length !== arr2.length){
return false;
}
let frequencyCounter1 = {}
let frequencyCounter2 = {}
for(let val of arr1){
frequencyCounter1[val] = (frequencyCounter1[val] || 0) + 1
}
for(let val of arr2){
frequencyCounter2[val] = (frequencyCounter2[val] || 0) + 1
}
console.log(frequencyCounter1);
console.log(frequencyCounter2);
for(let key in frequencyCounter1){
if(!(key ** 2 in frequencyCounter2)){
return false
}
if(frequencyCounter2[key ** 2] !== frequencyCounter1[key]){
return false
}
}
return true
}
same([1,2,3,2,5], [9,1,4,4,11])
개별로 for문이 2개 사용되었습니다. 이는 O(n)의 시간 복잡도를 가지겠습니다 더욱 나은 코드라고 할 수 있겠습니다. 원리는 각 배열안에 숫자의 빈도수를 확인합니다. 그리고 나서 두 배열을 서로 비교를 합니다.
다중 포인터 패턴
인덱스나 위치에 해당하는 포인터나 값을 만든 다음 특정 조건에 따라 중간 지점에서부터 시작 지점이나 끝 지점이나 양쪽 지점을 향해 이동시키는 것
정렬된 배열을 취하는(입력값으로 하는) sumZero라는 함수를 만들어라
단, 오름차순으로 배열이야한다. 이 함수는 합계가 0인 첫 번째 쌍,즉, 한숫자를 가져와 다른 숫자에 더하면 0이 되는 쌍을 찾습니다.
sumzero([-3,-2,-1,0,1,2,3]) // [-3,3]
sumzero([-2,0,1,3]) // undefined
sumzero([1,2,3]) // undefined해결책1 - 시간복잡도 O(n^2), 공간복잡도 O(1)
맨 왼쪽의 숫자를 한칸씩 오른쪽으로 옮기면서 모든 숫자와 비교하기
function sumZero(arr){
for(let i = 0; i < arr.length; i++){
for(let j = i+1; j < arr.length; j++){
if(arr[i] + arr[j] === 0){
return [arr[i], arr[j]];
}
}
}
}
sumZero([-4,-3,-2,-1,0,1,2,5])리팩토링 해결책2 - 시간복잡도 O(N), 공간복잡도 O(1)
맨 왼쪽의 수를 맨 오른쪽과 비교하고 합해서 0되면 출력
0보다 크면 왼쪽으로 0보다 작으면 왼쪽에서 두번째 숫자로 다시 비교 시작
function sumZero(arr){
let left = 0;
let right = arr.length - 1;
while(left < right){
let sum = arr[left] + arr[right];
if (sum === 0){
return [arr[i], arr[j]];
} else if (sum > 0){
right--;
} else {
left++;
}
}
}
기준점 간 이동 배열 패턴
sliding window 접근법으로 해석
창문을 하나 만들어야합니다. 아 창문은 단일변수, 하위배열, 또는 필요한 경우 시작 위치에서 시작하면 보통 왼쪽에서 오른쪽으로 이동합니다. 이렇게 창문을 이동시키면서 문제를 풀어가는 방식입니다.
예시문제
maxSubarraySum 라는 함수를 만들어라
이 함수는 정수 배열과 n을 입력받습니다. 그래서 정수 배열 안에서 n개으의 연속된 숫자 배열 중 합이 가장 큰 값을 반환합니다.
maxSubarraySum([1,2,5,2,8,1,5],2) // 10 (2,8)
maxSubarraySum([1,2,5,2,8,1,5],4) // 17 (2,5,2,8)
maxSubarraySum([4,2,1,6],1) // 6
maxSubarraySum([4,2,1,6,2],4) // 13
maxSubarraySum([],4) // null
해결책1 - 시간복잡도 O(n^2), 공간복잡도 O(1)
function maxSubarraySum(arr, num) {
if ( num > arr.length){
return null;
}
var max = -Infinity;
for (let i = 0; i < arr.length - num + 1; i ++){
temp = 0;
for (let j = 0; j < num; j++){
temp += arr[i + j];
}
if (temp > max) {
max = temp;
}
}
return max;
}
maxSubarraySum([2,6,9,2,1,8,5,6,3],3)리팩토링 해결책2 - 시간복잡도 O(N) 슬라이딩 윈도우
function maxSubarraySum(arr, num){
let maxSum = 0;
let tempSum = 0;
if (arr.length < num) return null;
for (let i = 0; i < num; i++) {
maxSum += arr[i];
}
tempSum = maxSum;
for (let i = num; i < arr.length; i++) {
tempSum = tempSum - arr[i - num] + arr[i];
maxSum = Math.max(maxSum, tempSum);
}
return maxSum;
}
maxSubarraySum([2,6,9,2,1,8,5,6,3],3)
분할과 정복 패턴
https://namu.wiki/w/분할%20정복%20알고리즘
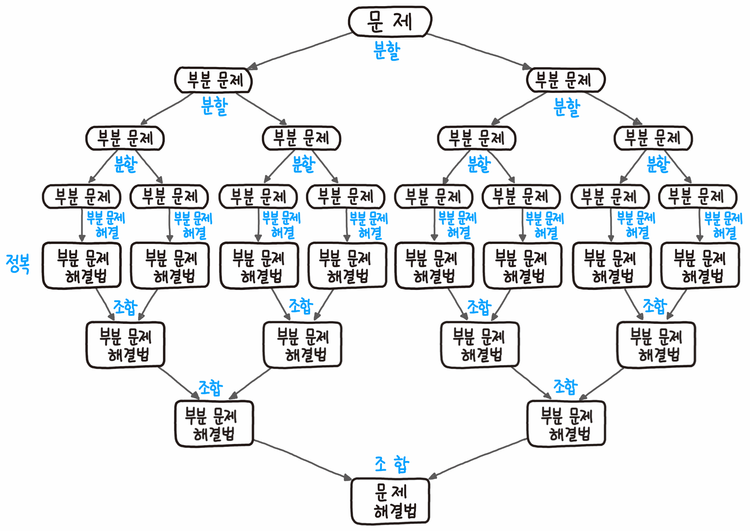
그림에서와 같이 분할 정복은 상단에서 분할하고 중앙에서 정복하고 하단에서 조합(Combine)하는 형태로 도식화 할 수 있다.
분할: 문제를 더이상 분할할 수 없을 때까지 동일한 유형의 여러 하위 문제로 나눈다.
정복: 가장 작은 단위의 하위 문제를 해결하여 정복한다.
조합: 하위 문제에 대한 결과를 원래 문제에 대한 결과로 조합한다.
search([1,2,3,4,5,6,],4) // 3
search([1,2,3,4,5,6,],6) // 5
search([1,2,3,4,5,6,],11) // -1정렬된 배열에서 원하는 숫자가 배열의 몇 번째에 있는 지 확인하는 함수 입니다.
해결책 1 시간복잡도 O(n)
function search(arr,val){
for(let i = 0; i< arr.length ; i++){
if(arr[i] === val){
return i;
}
}
return -1;
}위의 알고리즘을 선형 탐색이라고 합니다. 맨 앞의 숫자부터 하나씩 원하는 값인지 확인하는 알고리즘입니다.
해결책2
function search(array, val){
let min = 0;
let max = array.legth - 1;
while(min <= max) {
let middle = Math.floor((min+max)/2);
let currentElement = array[middle];
if (array[middle] < val){
min = middle + 1;
}
else if (array[middle] > val){
max = middle - 1;
}
else {
return middle;
}
}
return -1;
}
이진탐색 중간에서 부터 비교를 시작해서 좌 or 우 반만 비교하는 방법입니다. 시간 복잡도 O(log n) 분할과 정복의 예시로 쓰였습니다. 자세한 설명은 추후에 진행

