겁나 빠른 정렬 소개
합병 알고리즘은 중급 알고리즘이라고 할 수 있습니다. 기초 알고리즘(선택 삽입 버블) 보다는 빠르지만 코드가 직관적이지는 않습니다. 코드를 작성해야한다는 부담감보다는 알고리즘의 동작 원리를 이해하는 것으로 목표합시다. (추후에는 코드로...짜보는 것 까지 해야겠죠 ㅎㅎ)
Don't be scared!
주제
- 이전에 배운 기초 알고리즘(버블,선택,삽입)의 한계를 인지합시다.
- 합병, 퀵, 지수 정렬을 구현 구현해보려고 합니다.
그래서 무엇을 배울까?
- 기초알고리즘은 큰 규모에서는 안 좋은 효율을 보입니다. 시간복잡도만 생각해도 알 수 있겠죠.
- 기초 알고리즘의 시간복잡도는 O(n)이였다면 합병 정렬은 O(nlog n)을 가집니다. 상대적으로 합병 정렬이 더 빠르다고 할 수 있습니다.
합병 정렬
- 세가지의 조합이라고 볼 수 있습니다. 분할 정렬 합병. 세가지 모두 일어납니다.
- 분할 정복 알고리즘을 사용합니다.
- 시간 복잡도 O(nlog N)을 가집니다. , 공간복잡도는 O(n)입니다.
- 어떠한 상황에서도 위의 시간 복잡도를 보장합니다. -> 보장성이 높습니다.
(퀵소트의 경우 최악의 상황에서 O(n^2)의 시간복잡도를 가집니다)
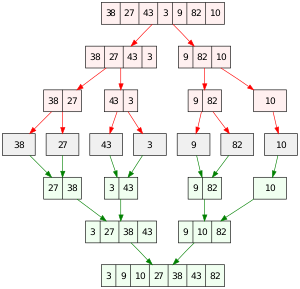
위의 그림에서 빨간선은 분할하는 모습이며 파란선이 병합하는 모습입니다.
배열 합병 소개 및 구현
- 정렬된 두 배열 합병을 담당할 함수를 구현합니다.
- 정렬된 두 함수가 주어지면, 헬퍼함수는 새로운 정련된 배열을 만들어 줍니다.
- 시간복잡도 O(n+m), 공간복잡도 O(n+m)을 가집니다.
(n과 m이란 함수에 첫번째 배열과 두번째 배열입니다. 입력이 두개의 배열이기 때문이죠)
의사코드
- 빈 배열을 만들어줍니다. 각 배열에서 가장 작은 값부터 시작합니다.
- 아직 살펴보지 않은 요소가 있다면,
- 만약 첫번째 배열의 값이 두번째 배열의 값보다 작다면, 첫번째 배열을 결과 배열에 집어 넣고, 다음 배열로 넘어갑니다.- 만약 첫번째 배열의 값이 두번째 배열의 값보다 크다면, 두번째 배열의 결과 배열에 집어 넣고, 다음 배열로 넘어갑니다.
- 배열 하나를 완료한 다음에는 다른 배열의 남은 값을 모두 넣습니다.
말로는 참 어렵습니다... 예시를 들어보겠습니다.
a배열 : [1,10,50] 과 b배열 : [2,14,99,100] 두개의 "정렬된" 배열이 있습니다.
1. 빈배열을 만듭니다. [] 이를 결과 배열이라 하겠습니다.
2. a배열 값 1 과 b배열 값 2를 비교합니다. 그리고 작은 수 1를 결과 배열에 넣습니다 (결과배열 [1]
3. a배열 값 10 과 b배열 값 2를 비교, 결과 배열에 2 추가 -> 결과 배열 [1,2]
4. a배열 값 10 과 b배열 값 14를 비교, 결과 배열에 10 추가 -> 결과 배열 [1,2,10]
이런식으로 비교를 진행하게 되는 방식입니다.
합병 정렬 작성하기
// Merges two already sorted arrays
function merge(arr1, arr2){
let results = [];
let i = 0;
let j = 0;
while(i < arr1.length && j < arr2.length){
if(arr2[j] > arr1[i]){
results.push(arr1[i]);
i++;
} else {
results.push(arr2[j])
j++;
}
}
while(i < arr1.length) {
results.push(arr1[i])
i++;
}
while(j < arr2.length) {
results.push(arr2[j])
j++;
}
return results;
}
merge([100,200], [1,2,3,5,6])
합병 정렬을 위한 빅오 복잡도
- 재귀를 사용하기 때문에 이에 대한 지식이 필요합니다.
- 코드가 길지는 않지만 이해하기 조금 어려울 수도 있습니다.
// Merge function from earlier
function merge(arr1, arr2){
let results = [];
let i = 0;
let j = 0;
while(i < arr1.length && j < arr2.length){
if(arr2[j] > arr1[i]){
results.push(arr1[i]);
i++;
} else {
results.push(arr2[j])
j++;
}
}
while(i < arr1.length) {
results.push(arr1[i])
i++;
}
while(j < arr2.length) {
results.push(arr2[j])
j++;
}
return results;
}
// Recrusive Merge Sort
function mergeSort(arr){
if(arr.length <= 1) return arr;
let mid = Math.floor(arr.length/2);
let left = mergeSort(arr.slice(0,mid));
let right = mergeSort(arr.slice(mid));
return merge(left, sright);
}
mergeSort([10,24,76,73])
시간 복잡도가 왜? n * log n 일까요
O(log N)은 N 증가에 따른 분할 수 입니다.
(예를들어 값 8개를 갖는 배열의 경우 3번의 분할이 필요합니다)
(예를들어 값 16개를 갖는 배열의 경우 4번의 분할이 필요합니다)
매번 분할 할때마다 합병을 위해서는 O(n)이 필요합니다.
([3,8][4,6] 를 합병하려면 3번을 비교해야하죠)
([1,3,8][2,4,6] 를 합병하려면 5번을 비교해야하죠)
이미 정렬된 배열을 입력 받기 때문에 가능한 시간복잡도 입니다.
두개가 모두 정상 작동해야하기 때문에 전체 시간 복잡도는 N*log n 이 형성 됩니다.


