
문제해결
N개의 원소들로 이루어진 집합 U에서 중복을 허용하여 숫자 4개를 뽑고, 뽑은 수를 x, y, z, k라고 했을때 x + y + z = k 를 만족하는 k의 최대값을 찾는 문제이다. 가장 노멀한 방법은 N에서 임의로 4개의 수 조합을 전부 다 뽑아보는 경우인데 N은 최대 1,000이므로 당연히 시간초과가 난다.
x + y + z = k 를 x + y = k - z 로 바꿔서 생각해보면 x + y값을 담은 배열을 새로 생성하고 그 안에서 k - z를 만족하는 k의 최대값을 찾으면된다. 하지만 이 방법도 x + y 배열을 탐색할때 단순한 반복문으로 탐색하면 시간초과가 나므로 정렬한 후에 이분탐색을 하는 방법으로 답을 찾아야 한다.
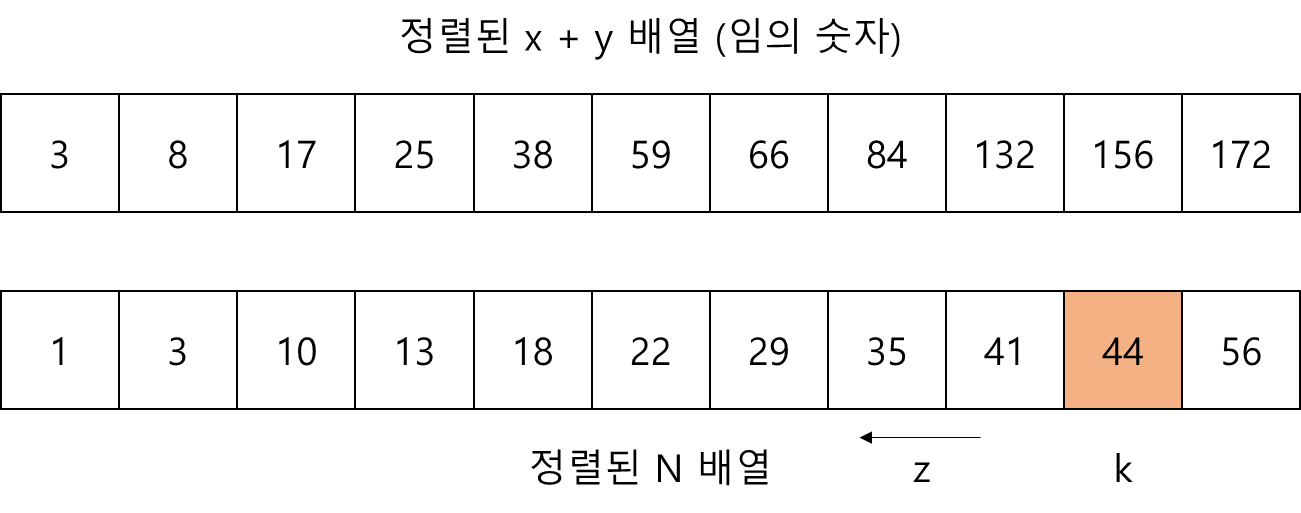
(x + y배열은 시각적인 도움을 주기위해 넣었고 임의의 수가 들어가있다.)
k를 한개 선택하고 k보다 작은쪽을 전체탐색하며 z를 대입했을때 x + y의 배열에서 k - z와 같은 값이 있는지 이분탐색으로 찾으면된다. k를 한칸씩 줄여나가다가 같은 값을 찾을경우 N배열은 정렬되어 있으므로 그때의 k값이 최대이다.
sort, 이분탐색
시간복잡도
x + y의 배열 크기는 N(N + 1)/2(= N²) 이므로 배열의 이분탐색을 하는데 걸리는 시간은
log N² 이고, k - z를 전체 탐색하는데 이중반복문을 사용하면 걸리는 시간은 N(N + 1) / 2
(= N²) 이므로 전체 시작복잡도는 N²log N² 이다. (N <= 1000)
코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int N, num[], sum[], count = 0;
N = Integer.parseInt(br.readLine());
num = new int[N];
sum = new int[N * N];
for (int i = 0; i < N; i++) {
num[i] = Integer.parseInt(br.readLine());
}
Arrays.sort(num);
for (int i = 0; i < N; i++) {
for (int j = i; j < N; j++) {
sum[count++] = num[i] + num[j];
}
}
Arrays.sort(sum, 0, count - 1);
for (int i = N - 1; 0 <= i; i--) {
for (int j = i; 0 <= j; j--) {
if (Arrays.binarySearch(sum, 0, count - 1, num[i] - num[j]) < 0) continue;
bw.write(String.valueOf(num[i]));
bw.flush();
bw.close();
return;
}
}
}
}
