아래 링크를 보고 내용 다시 정리하기!
Exploratory Data Analysis
데이터 분석과 시각화의 맥락에서 중요한 데이터 유형은 네가지 (nominal, ordinal, interval, ratio)이다.어떤 분석의 방식에는 특정 형식만 지원하는 경우가 있기도 하고, 자신이 분석하고자 하는 데이터의 형식을 통해 문제를 잘 정의하거나 적합한 해결방식을 제안할 수 있기 때문이다.
1. nominal data (명목 자료)
- values represent discrete units
- changing the order of units does not change their value.
nominal data는 nominal(이름과 관련한)이란 수식어처럼 여러 category들(예: 청팀, 백팀, 홍팀)들 중 하나의 '이름' 에 데이터를 분류할 수 있을 때 사용된다.
nominal data는 순서가 의미없다.
청팀, 백팀, 홍팀이나 홍팀, 백팀, 청팀이나 같다.
특히, nominal data가 두 개의 범주 중 하나에 속하는 경우 (남자 vs 여자) dichotomous data(이분 자료)라고 부른다.
nominal data를 categorical data (범주형 자료)라 부르기도 한다.
2. ordinal data (순서 자료)
- values represent discrete and ordered units.
- distance between units is not the same.
데이터가 속하는 category에 순서가 있는 경우 ordinal data라고 한다.즉, 순서가 있는 명목 자료라고 할 수 있다.
예를 들어 청팀이 이길 가능성에 대한 설문조사를 하는 경우 답변을 “5. 매우 높다. 4. 높다. 3. 중립, 2. 낮다. 1. 매우 낮다."로 디자인할 수 있다.
nominal data와 마찬가지로 counting을 하고 percent로 표현해도 좋다. (매우 높다: 33%, 높다: 19%…)
단, 평균에 대해서는 조심해야 한다. 매우 높다에 5를, 높다에 4를 할당한 것처럼 그 각각의 항목에 엄정한 수학적/과학적 의미가 없는 경우 순서의 간격이 일정하지 않을 수 있기 때문이다. 매우 낮다와 낮다 사이의 간격이 매우 높다와 높다 사이의 간격과 같지 않을 수 있기 때문이다.
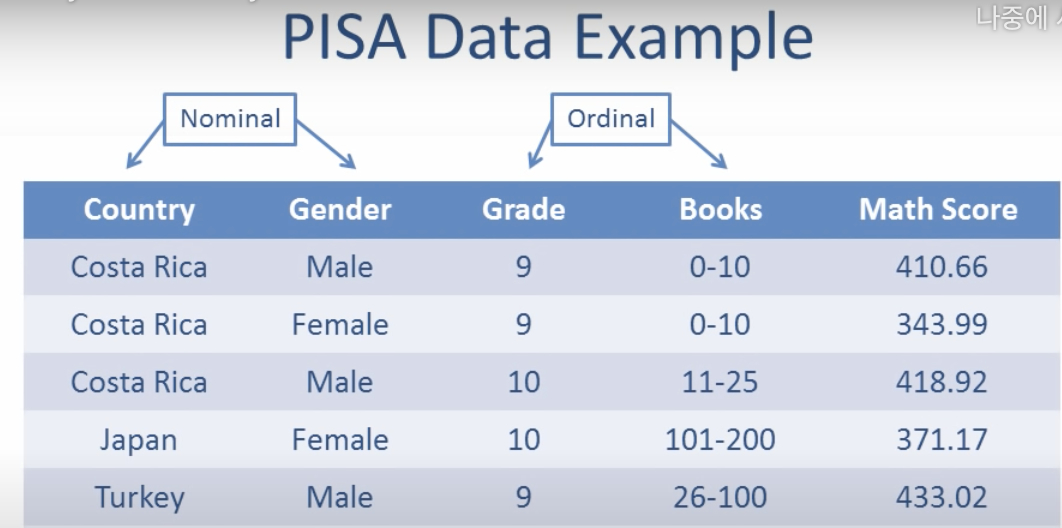
이처럼 구간으로 보이는 books의 경우, 구간의 사이가 같기 때문에 ordinal이라고 할 수 있다.
3. interval data (구간 자료)
- ordered units with intermediate values.
- distance between units is the same.
- No absolute zero.
- origin is arbitary.
- a person with an IQ score of 160 is NOT twice smarter than someone who have an IQ score of 80.
기본적으로 하루 중 특정 시점을 나타내는 시각은 interval data다.
이처럼 데이터의 연속된 측정 구간 사이의 간격이 동일한 경우 interval data라고 부른다. (11:00와 11:05의 차이는 15:55과 16:00의 차이와 동일이다.)
interval data는 numeric value를 가지므로 다양한 연산을 수행해도 된다.
단, 절대적 원점(zero point)이 없다. 무슨 말이냐면 00:00이라는 자료의 값이 측정한 시간의 값이 없다는 게 아니라 그냥 자정에 시간을 측정했다는 뜻.
4. ratio data (비율 자료)
현재 시각이 13:30인데 내가 시계를 보고 13:00부터 계산해서 “30분” 기다렸네 할 때 “30분"은 ratio data이다.
ratio data의 경우 interval data와 다르게 절대적 원점(meaningful zero point)이 존재하며 interval data에서 00:00이라는 값은 (기다린 시간이) “빵”초 라는 뜻이다.
나이, 돈, 몸무게 이런게 주로 ratio data로 다루어 진다.
+) discrete vs continuous (링크 상관 없이 찾아본 것)
interval이나 ratio 자료는 이산형(discrete)이나 연속형(continuous) 둘 중의 하나의 속성을 갖게 된다.
측정값이 정수로 딱딱 떨어지는 경우 이산형이고 연속된 무수히 많은 값 중 하나를 가질 수 있는 경우 연속형이 된다.
연속형 데이터는 실제 표현될 때 적당히 반올림 되어 표현된다. 현실에서 측정 혹은 이해하고자 하는 변수는 종종 하나 이상의 data type을 갖게 되며 변수의 data type은 어떤 측정(수집) 방법을 택하느냐에 따라 결정된다. 나이를 예로 들자면 나이(본질적으로 ratio data)는 ratio data로 수집될 수도 있지만 ordinal data로 수집될 수도 있다. (나이가 속한 그룹을 선택하는 방식으로 데이터를 수집한 경우로, 0~9세, 10세~19세 등으로 일정한 구간으로 나눈 경우.)
반면, nominal이나 ordinal data(둘 다 category 유형 데이터)을 interval이나 ratio data로 수집할 수는 없다. (청팀, 백팀, 홍팀으로 분류되는 데이터를 interval/ratio data로 수집할 수 없음)
데이터 측정은 주어진 데이터의 본질적 속성보다 덜 정교한 수준(예: interval/ratio를 nominal/ordinal로) 측정할 수는 있어도 더 정교한 수준(예: nominal/ordinal을 interval/ratio)으로 측정할 수는 없다.
Descriptive Statistics
어떤 데이터인지에 따라 데이터들의 특성을 '잘' 설명해줄 수 있는 방법이 다르다.
Central tendency
중앙으로 얼마나 몰려있냐? : 평균, 중앙값(Q2), 최빈값
값들이 편향되어 있는 경우 데이터들의 특성을 설명하기 어려움.
Variability
어떻게 분포되어 있냐? : 범위(max - min), std(표준편차값), 사분위범위(Q3-Q1)
Nominal data
Ordinal data
Continuous data
데이터 요약
Categorical Summary
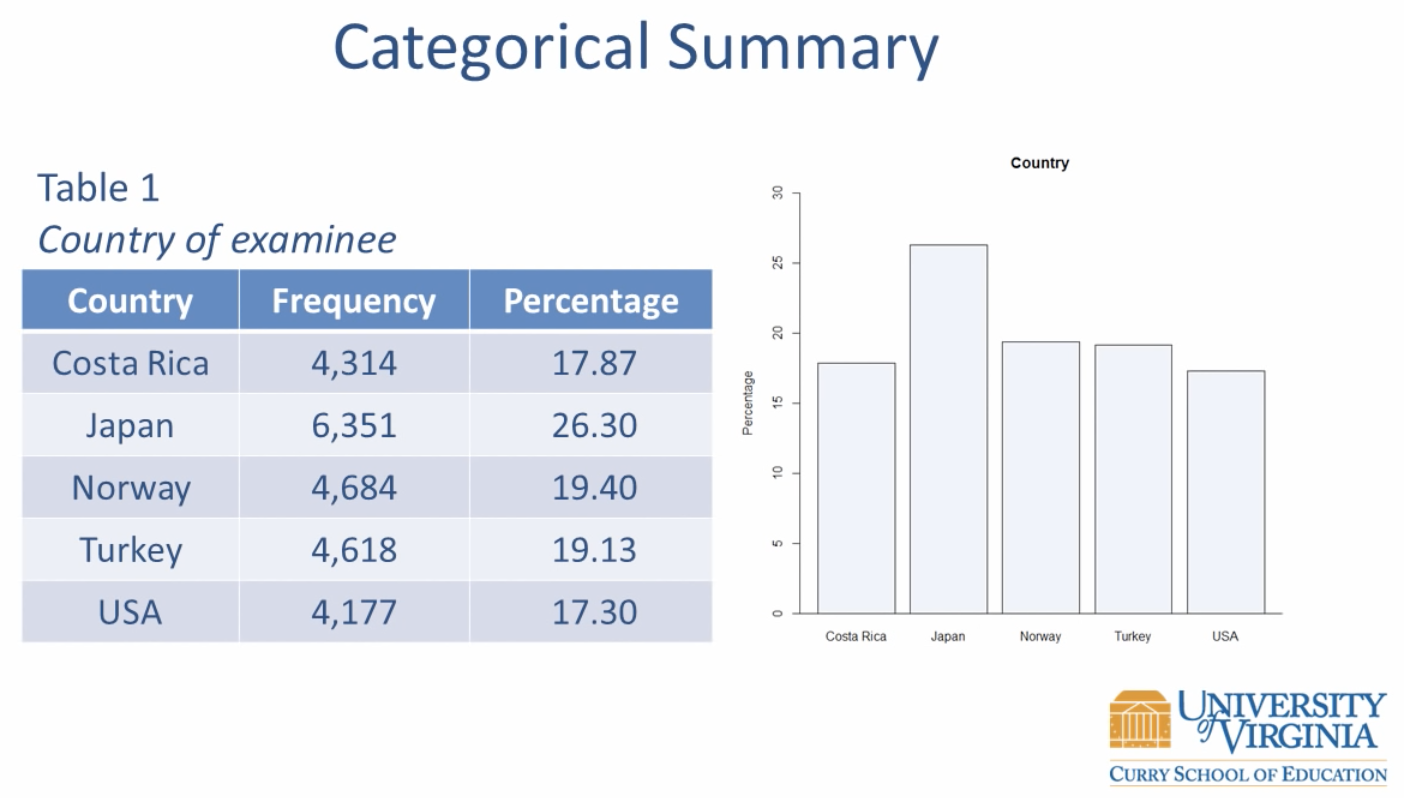
이 데이터는 빈도와 퍼센트라는 명목 데이터로 구성되어 있다. 막대 그래프는 시험에 참가한 국가별 참가자들의 빈도와 퍼센트를 나타내준다. 막대그래프의 중요한 특징은 각 막대들은 서로 연관성이 없으며 서로 영향을 주고 받지 않는다는 것이다. 막대 그래프는 히스토그램과 달리 막대들이 서로 간격을 둔 채 떨어져 있는 것으로 나타난다. 이러한 데이터 요약은 데이터들이 카테고리화되어 있는 데이터라는 것을 알려준다. (연속형이 아니다!)
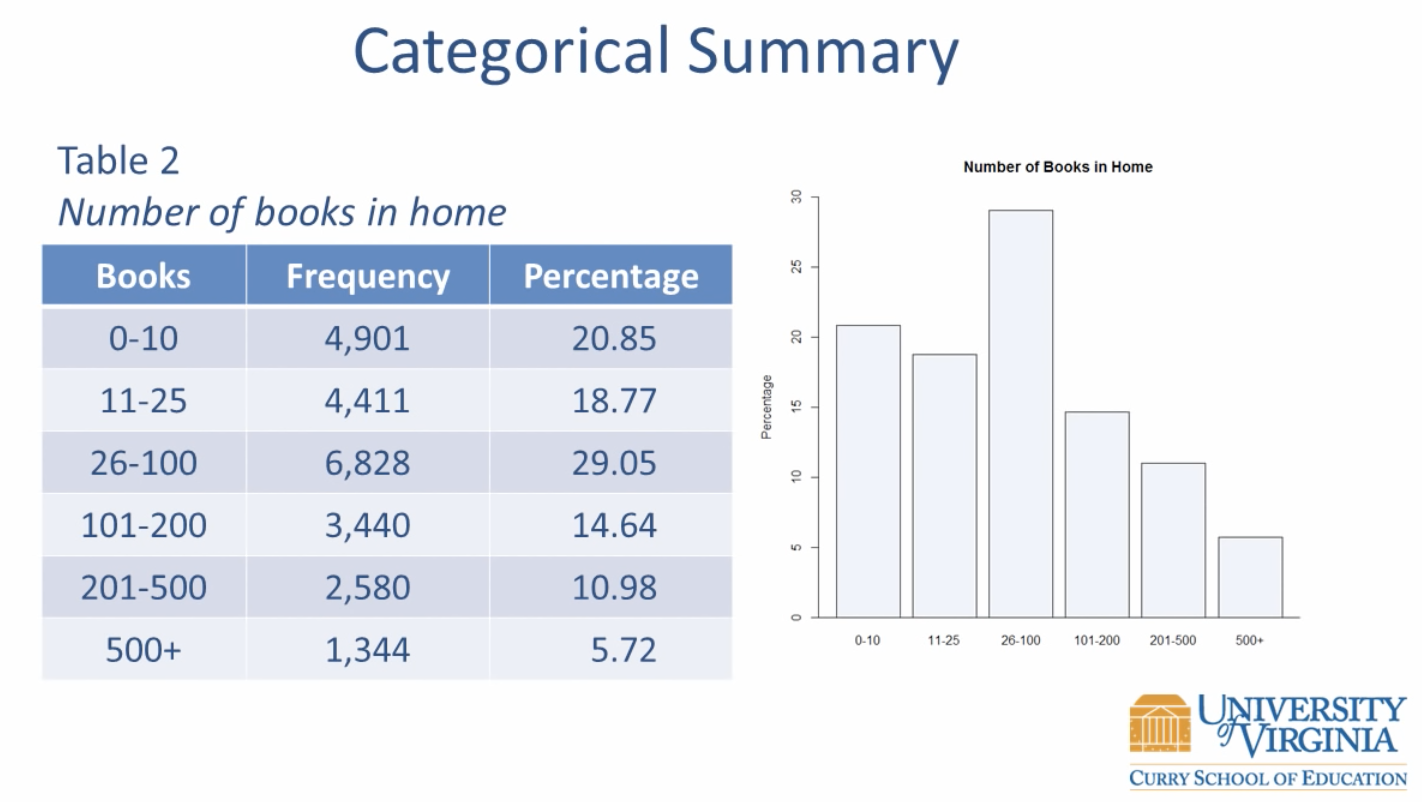
이 데이터 역시 빈도와 퍼센트로 나타나져있지만 순서가 정해져있다. 막대의 위치를 바꾸게 되면 막대의 의미(몇 번째로 크고작은 카테고리에 있는가)를 바꾸게 된다. 그러므로 0-10,11-25,...,500+의 순서대로 나타내어 주거나 반대로 500+,201-500,...,0-10으로 나타내주어야한다. 이러한 점을 통해 이 데이터는 순서 데이터라는 것을 알 수 있다.
Continuous Summary
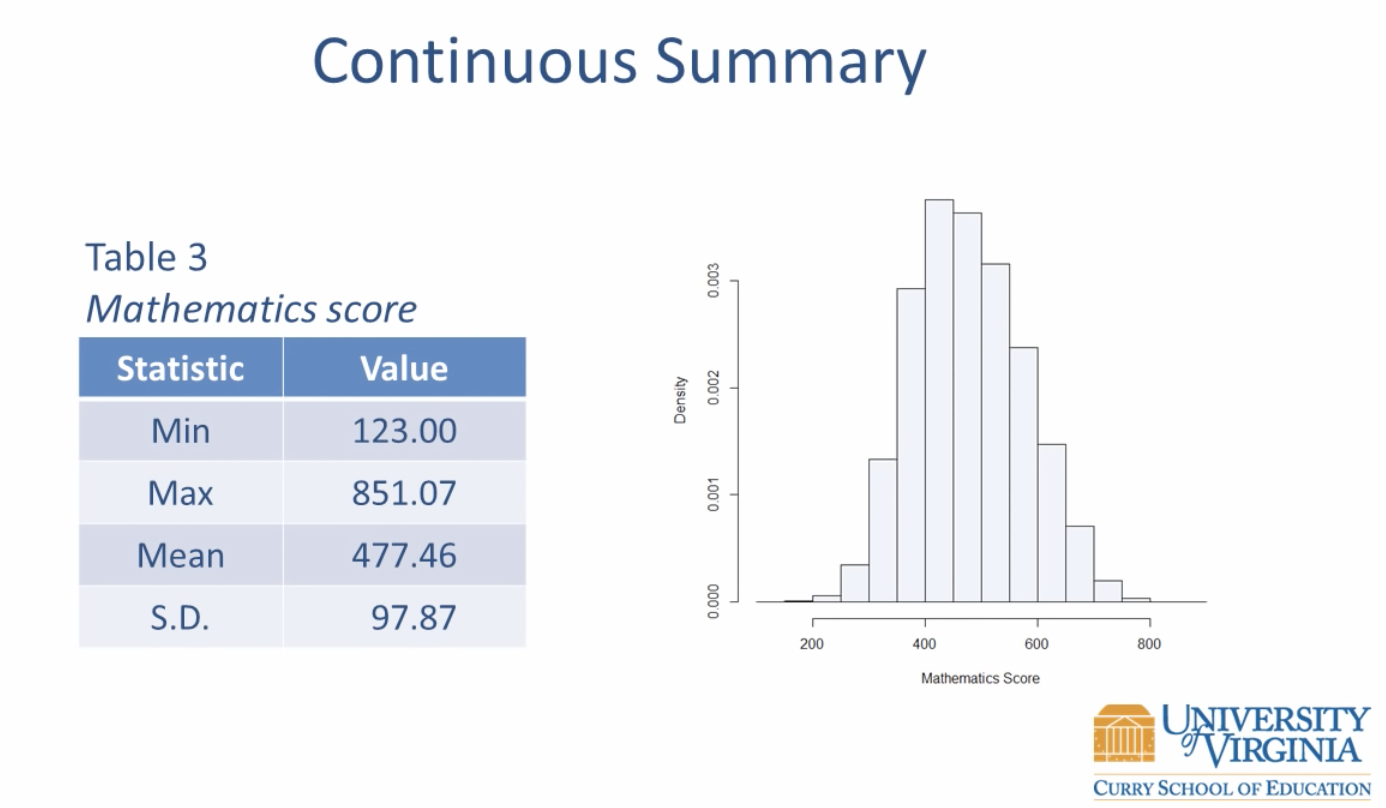
연속형 데이터를 볼 때 사용되는 히스토그램은 어떠한 변수에 대해서 구간별 빈도수를 나타낸 그래프이다. 가로축은 구간을 , 세로축은 빈도를 나타내며 도수분포를 그림으로 나타낸 것인데(즉, 도수분포표를 그림으로 나타낸 것이다.), 막대그래프와 달리 막대 사이의 간격이 없으며 평균과 분포를 아래처럼 비교적 시각적으로 뚜렷하게 볼 수 있다는 장점이 있다.
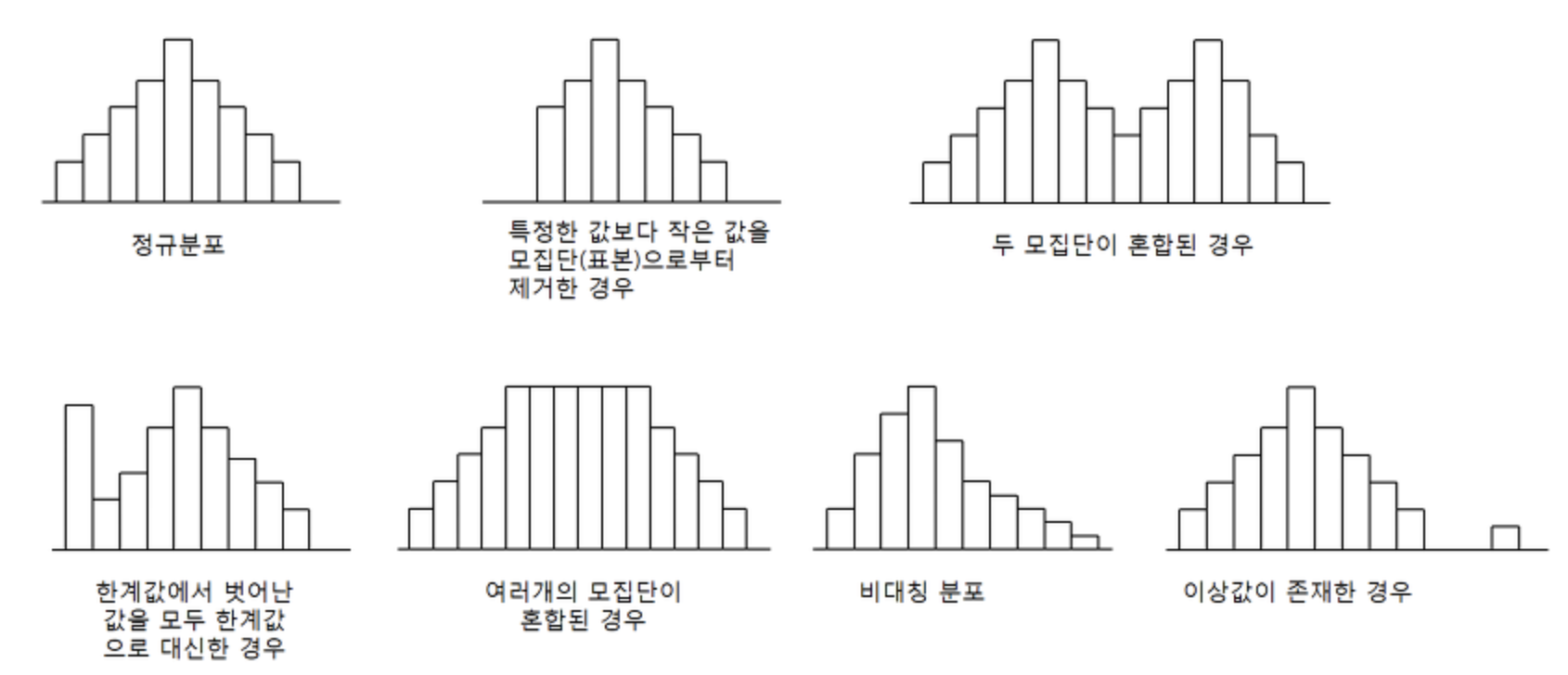
하지만 히스토그램은 이상값을 보기에는 적절하지 않다.
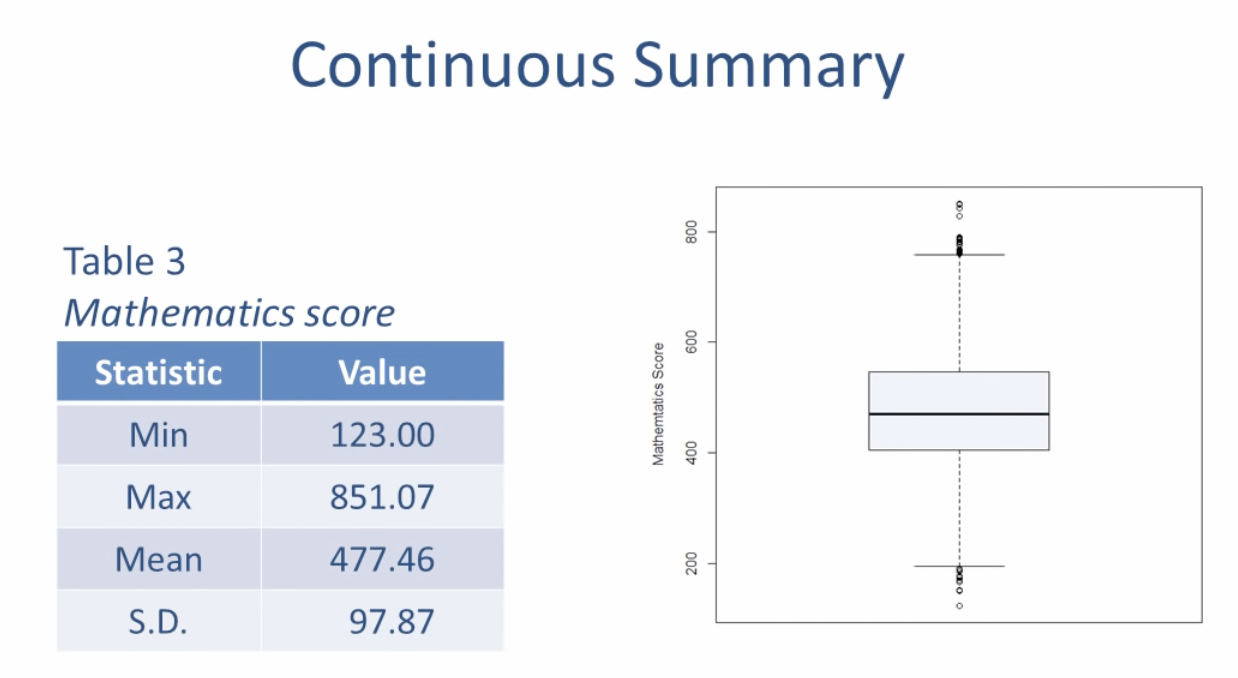
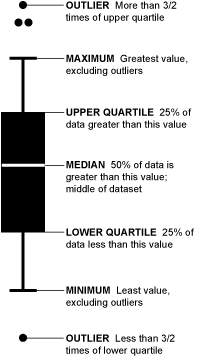
박스그래프(box plot)는 히스토그램의 문제점을 보완할 수 있는 연속형 자료를 볼 때 사용할 수 있는 그래프이다. 박스그래프를 해석하는 방법은 아래와 같다.
박스그래프는 central tendency와 variability,skewness(치우쳐진 정도)를 확인할 수 있는 그래프이다. 다만 최빈값을 알기 어렵다.
히스토그램과 박스그래프는 각기 장단점이 있기 때문에 EDA를 할 때 두 개를 다 그려보는 것이 좋다고 한다. 만약 이상값이 있는 unimodal(단봉) data라면 박스그래프가 더 적합하고 bimodal(봉이 1개 이상)인 데이터라면 히스토그램이 박스그래프보다 더 적합하다.
두 변수의 관계 살펴보기
두 변수가 어떠한 상관관계가 있는지 살펴봐야할 수도 있다. 이때는 아래와 같은 질문들을 할 수도 있다.
두 변수의 관계를 살펴볼 때는 이제 두 변수가 어떤 데이터 형태인지를 파악해야한다. 하나가 categorical한 데이터인데 하나가 continuose한 데이터라면 각 데이터를 표현하는 방식이라던가 어떻게 상관관계를 밝혀야하는지, 어떻게 대응되는지를 살펴보아야 정확한 상관관계를 밝힐 수 있기 때문이다.
두 변수의 관계를 살펴볼 때 필수적인 조건은 각각의 참가자들은 두 변수에 대한 값을 가지고 있어야 한다는 것이다. 그렇지 않으면 분석에 사용되기 어렵다.
다음의 예를 통해 두 변수 사이의 관계를 살펴보자.
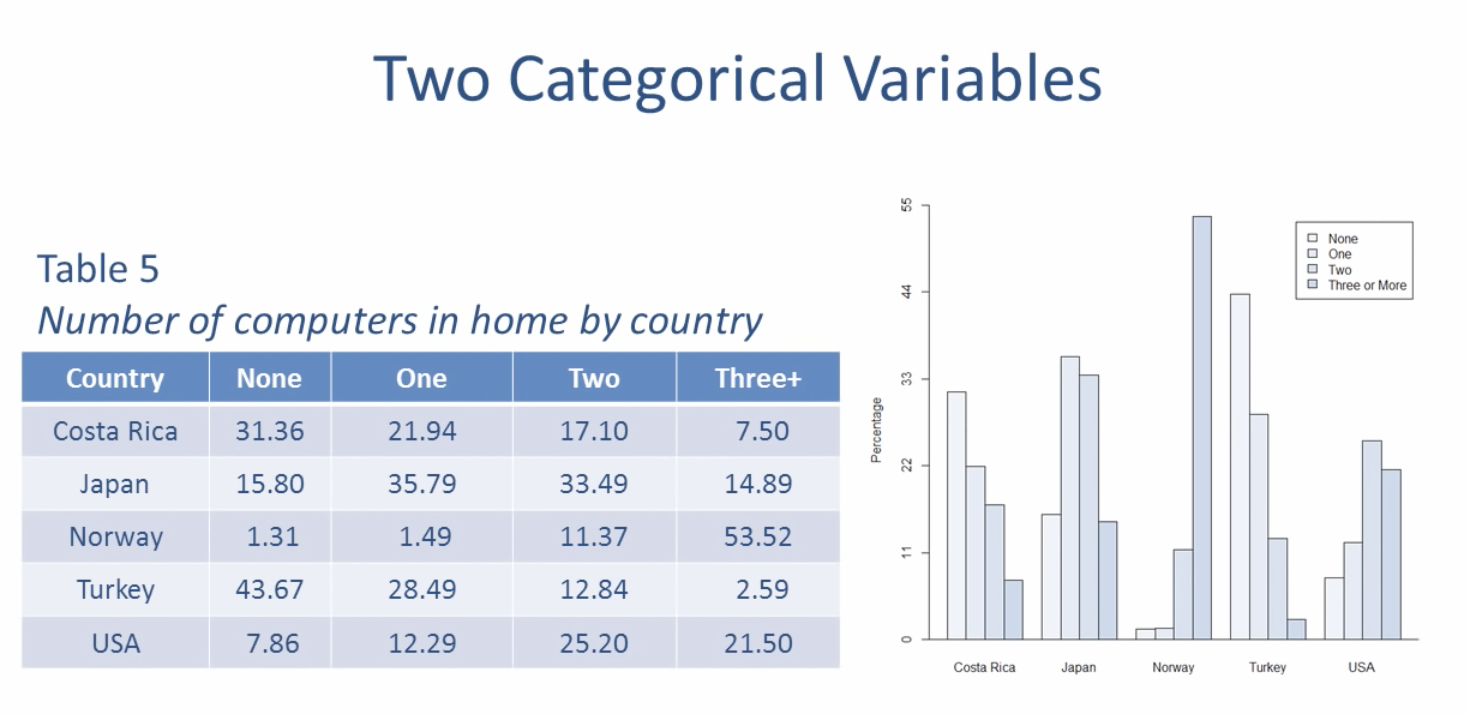
표에서는 집에 있는 컴퓨터의 개수는 국가에 따라 다르다는 것을 확인할 수 있다. 코스타리카의 많은 가정들은 컴퓨터를 가지고 있지 않았고 노르웨이는 세 대 이상의 컴퓨터를 가지고 있는 경우가 많았다. 경제적이거나 사회적인 요인과 컴퓨터의 대수는 차이가 있다고 가정해볼 수 있는 것이다. 표에서 나타난 변수 중 하나는 행을 의미하게 되고 다른 변수는 열을 의미하게 된다.
두 카테고리 변수의 관계 나타내기
fee coefficient
Cramer's V
카이제곱검정
두 연속형 변수의 관계 나타내기
산포도
하나는 카테고리 변수이고 하나는 연속형 변수일 때 관계 나타내기
side-by-side box plot
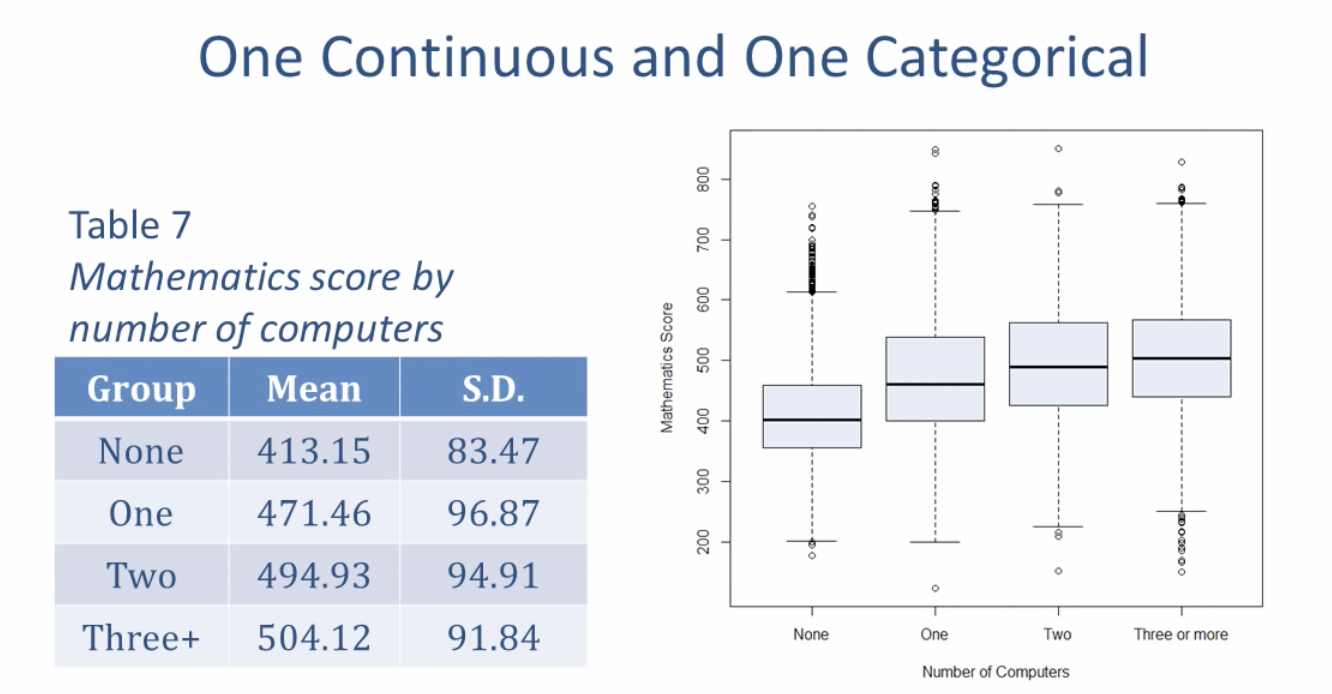
(이 그림에서는 수학점수(연속형, 여기에서는 등급이 아니라 1점 2점 이런 식인 것 같다.)와 집에 있는 컴퓨터의 개수(카테고리 변수)의 상관관례를 나타내준다. 표에서도 mean이 더 커지고 이를 그래프에서도 확인할 수 있다.
생각해보기
데이터의 종류와 그것을 어떻게 시각적으로 표현하느지를 살펴보았다. 이러한 과정에서 더 생각해볼수 있는 지점들이 있다.
(IQR = Interquartile range, 사분범위 = Q3-Q1)
이러한 지점들은 EDA를 하면서 알게되는 데이터의 특성에 따라 답이 달라지게 된다.
이상값이 나왔을 때 먼저 생각해봐야하는 것은 데이터를 입력할 때 잘못 입력을 했는지 확인해보는 것이다. 만약 그렇지 않았다면 데이터의 보편적인 특성을 더 잘 보여줄 수 있는 중앙값이나 최빈값을 사용해보는 것을 고려하는 것이 바람직하다. 왜냐하면 이상값은 평균이나 표준편차(분산의 정도 또는 자료의 산포도를 나타내는 수치)에 영향을 주기 때문이다.
만약 두 변수의 관계를 살펴보는데 이상치가 있는 경우 그 이상치가 어디에 있는지 살펴보아야한다.
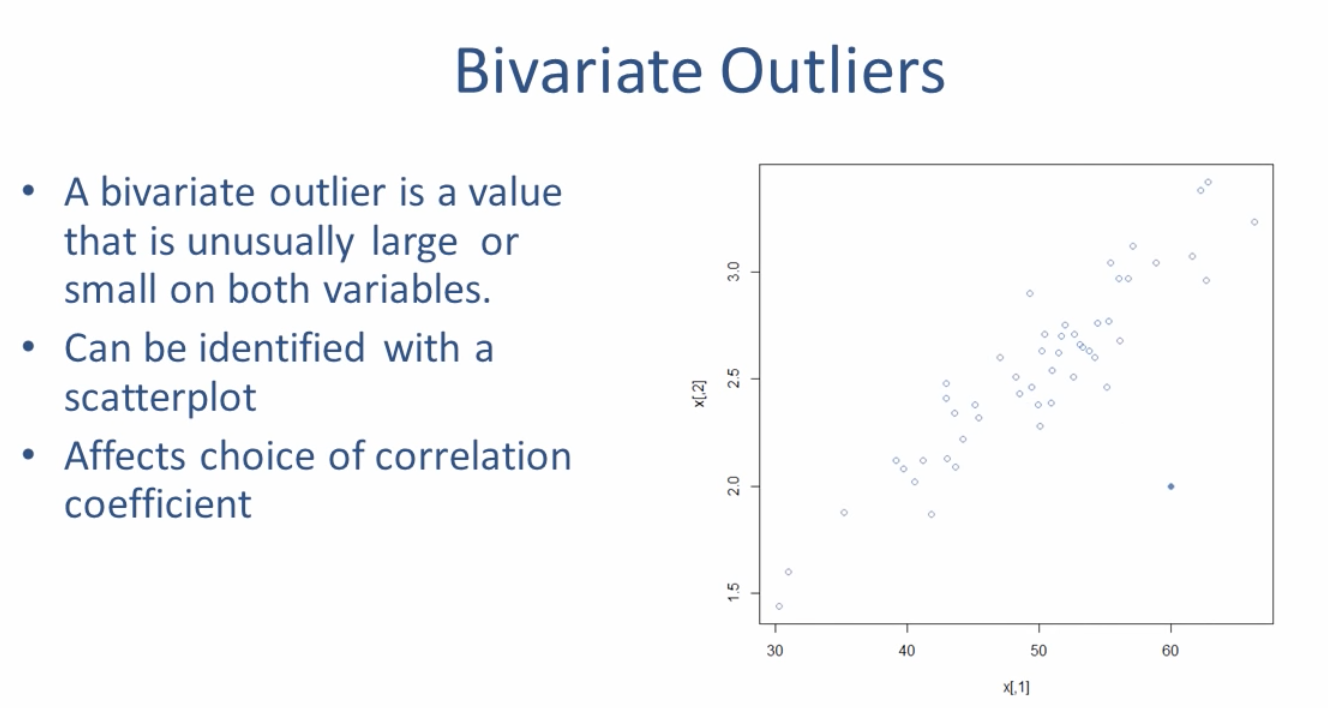이 경우에는 산포도가 쉽게 알려주는데 위의 그림에서 톡 떨어져나와있는 점 하나가 바로 이상치이다.
쉬어가기
박스그래프를 만들고 소프트웨어라는 표현을 만든 존 투키는 시각적인 표현은 제안하고 문제에 대한 답 이상을 말하는 데에 최고의 수단이라고 했다. 또한 통계학을 하는 것은 마치 자신이 답을 찾았는지를 확신할 수 없는 상태에서 십자말풀이를 하는 것과 같다고 했다.
