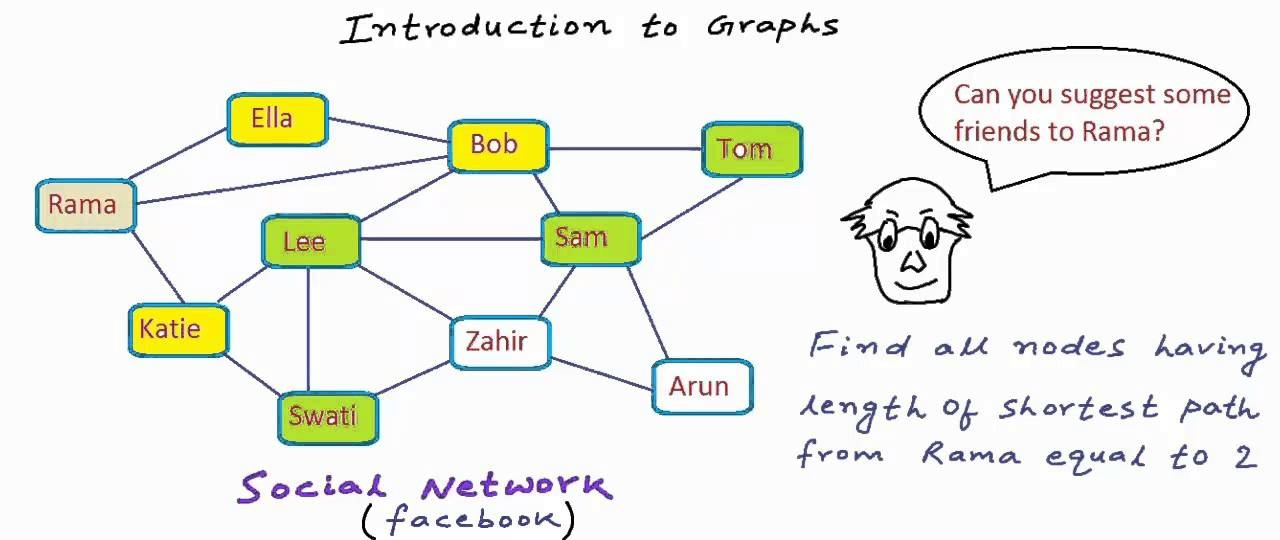
그래프 자료구조

• 트리형 자료구조와 연결지어 자주 등장하는 자료구조이다.
• 노드 간에 연결될 수 있다는 점을 제외하고 트리와 비슷하며 루프를 형성할 수도 있다.
• SNS, 도로 상의 차량 검색, 운송시스템 등 object 간의 관계를 표현할 때 유용하다.
  
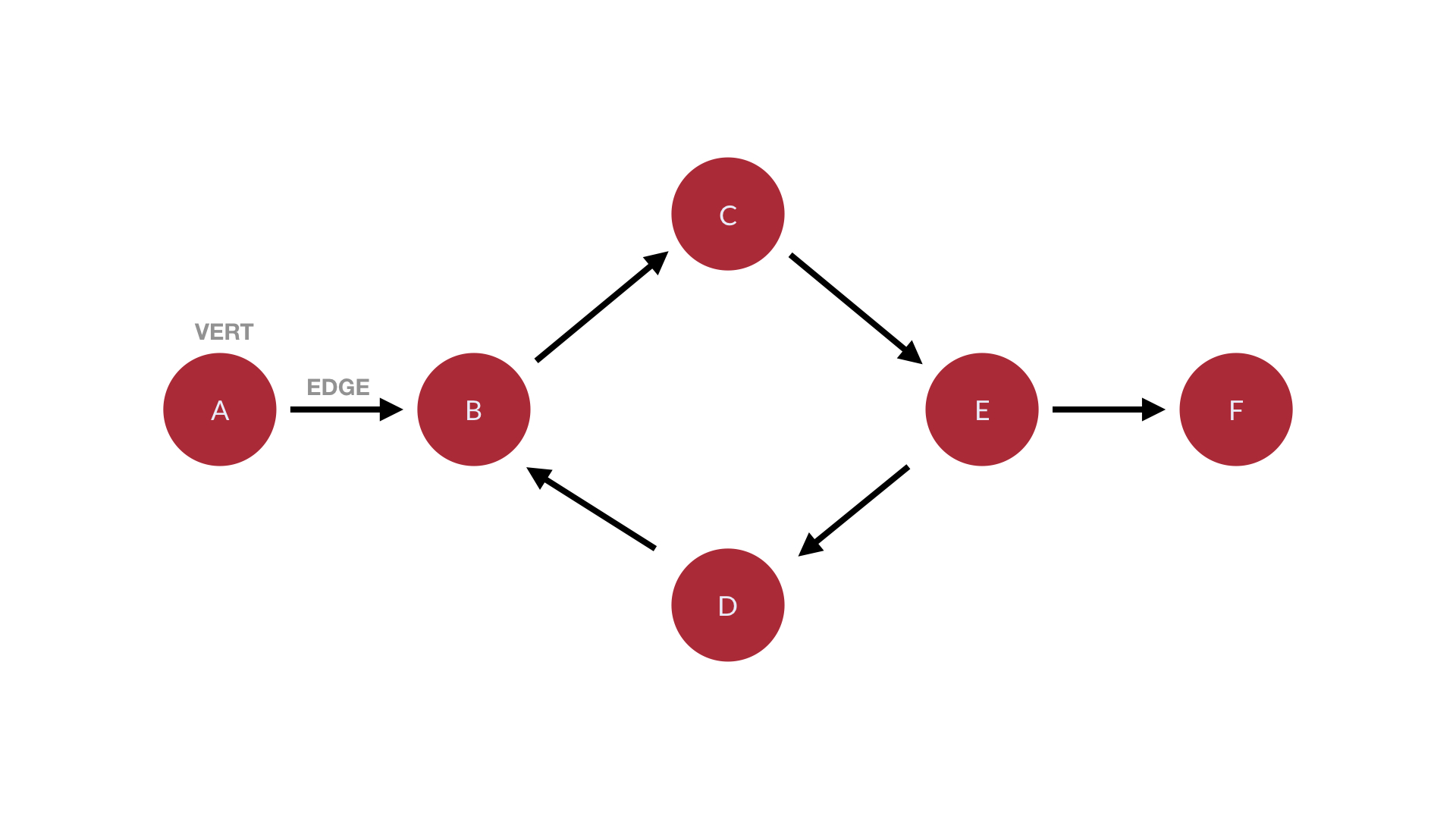
  일반적으로 그래프는 위의 그림처럼 node(vert 혹은 정점)와 edge(간선)으로 연결되어 있다.

그래프와 트리의 특징

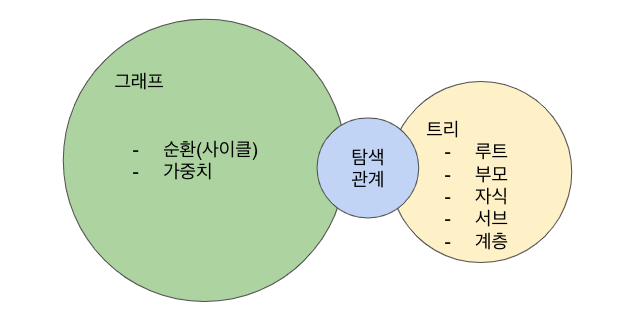
• 그래프는 노드의 관계를 표현한다.
• 트리는 노드 간의 계층을 표현한다.
• 그래프와 트리는 서로 다른 개념이라는 것을 알아야한다! 특히, 트리에만 있는 계층 개념으로 구분할 수 있다.

그래프의 유형

방향성 vs 무방향성

그래프가 방향성을 가지고 있는지의 유무에 따라 directed 와 undirected로 나눌 수 있다.

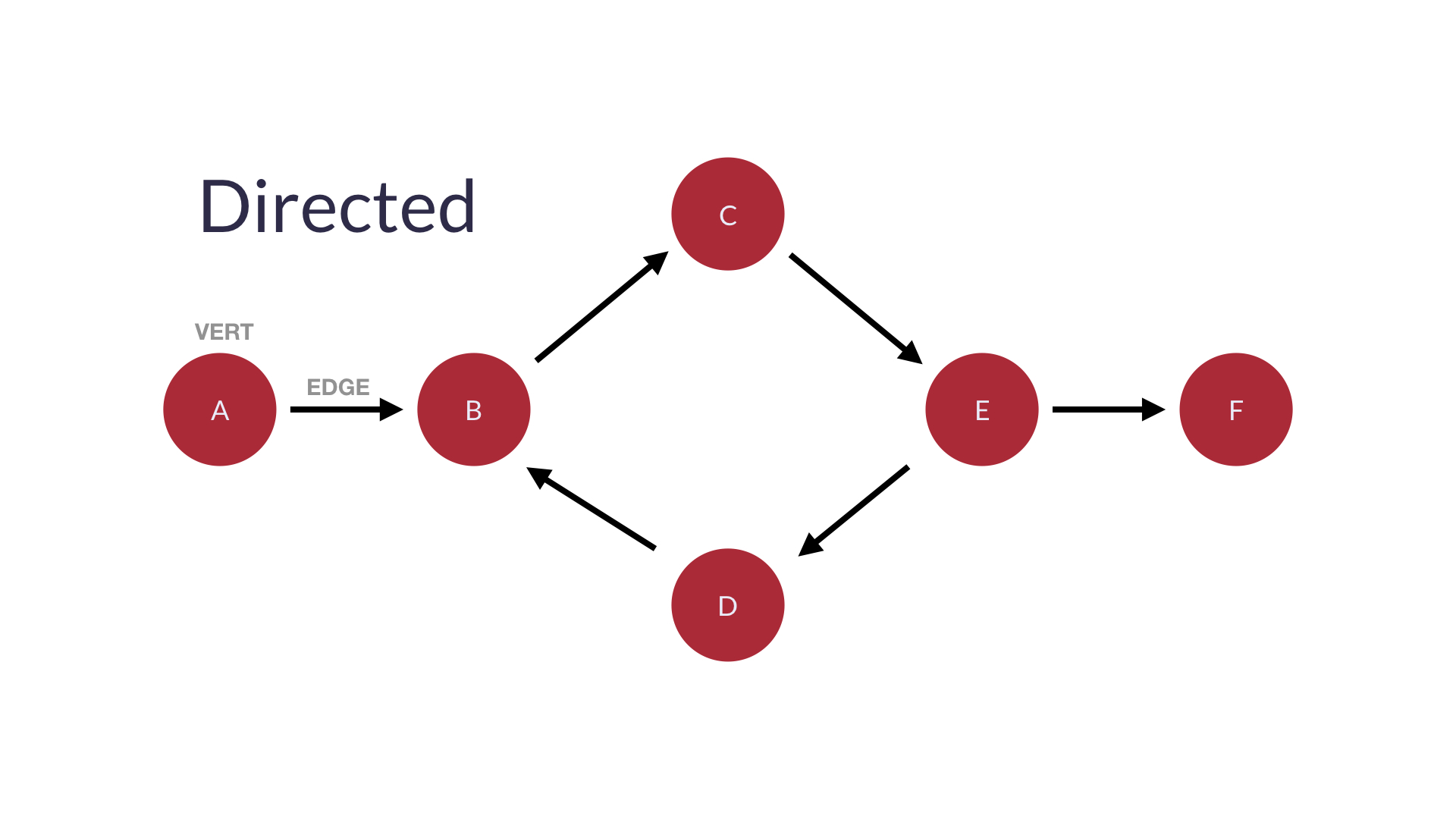
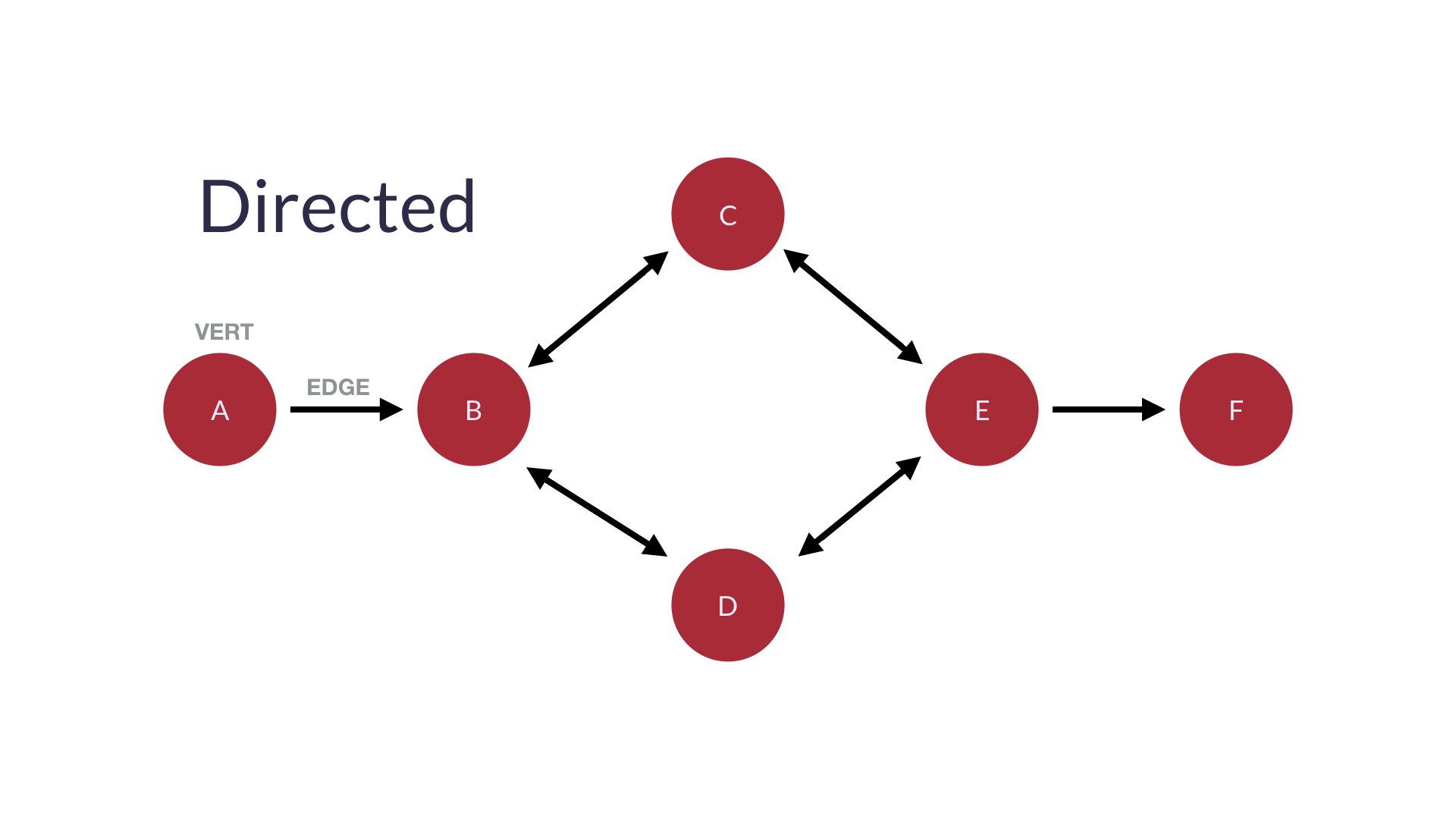
그래프가 한 쪽 방향(one-way)로 설명될 수 있다면 directed 그래프가 가장 적합하다.
방향성 그래프는 순서가 정해져 있어 마지막 노드(leaf)가 있다.
위 그래프의 리프는 F이다.

한편, 그래프는 양쪽 방향으로도 설명될 수도 있다. (bidirectional)
무방향과 양방향은 사실상 같다고도 볼 수 있다.
무방향성은 방향이 따로 지정되어 있지 않아 양방향성과 같은 특성을 가지고 있기 때문이다.
모든 간선들이 양방향성을 가지고 있다면 무방향성을 가지고 있다고 할 수 있다.

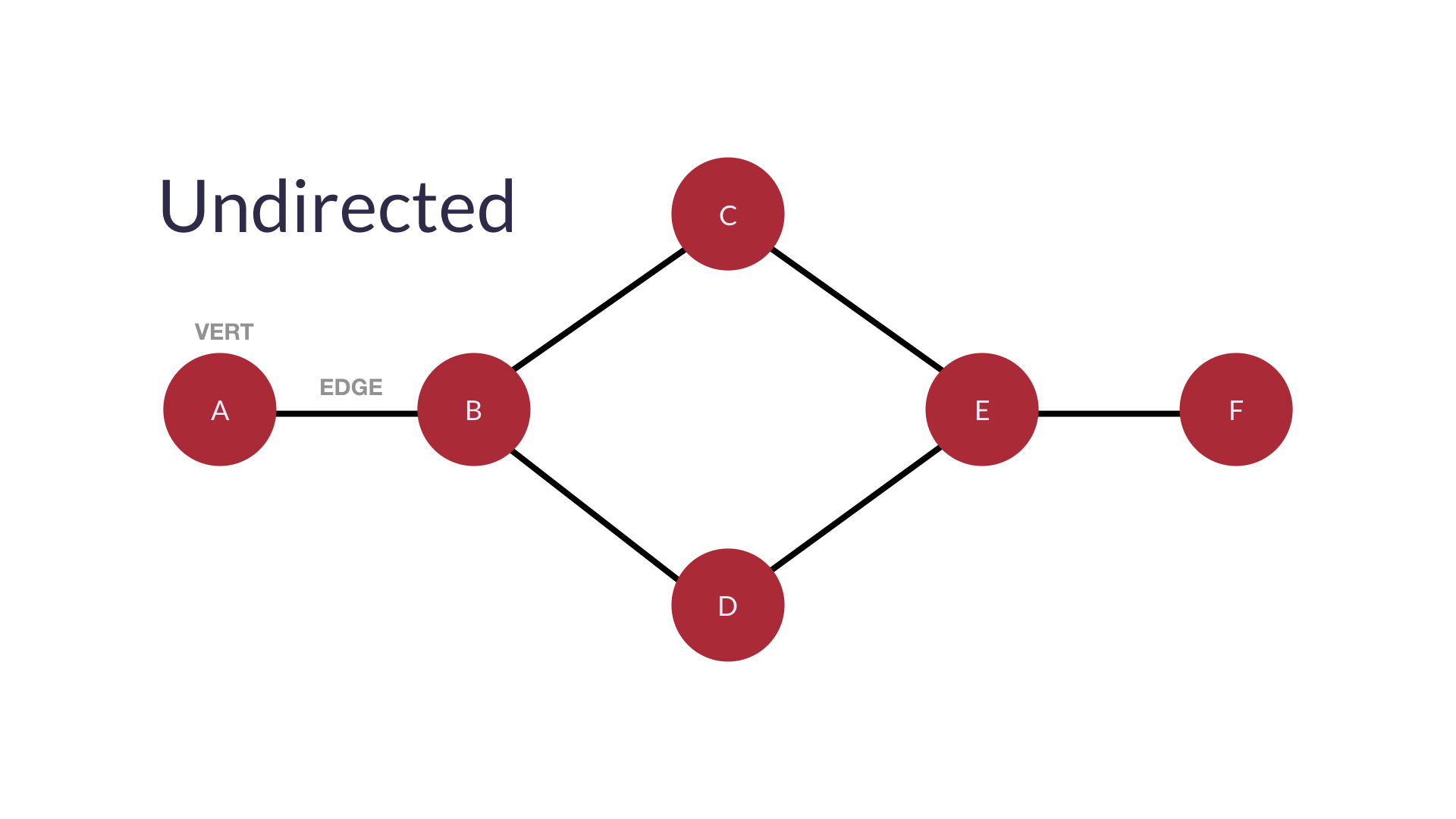
위와 같은 그래프가 무방향성이다.
관계의 목적이 상호 교환이라면 undirected 그래프가 가장 적합하다.
무방향성은 화살표의 방향이 따로 지정되어 있지 않다.
간선으로 연결된 노드들끼리는 서로 인접(adjacent)해있다고하며, 이웃(neighbor)라고 부른다.

순환성 vs 비순환성

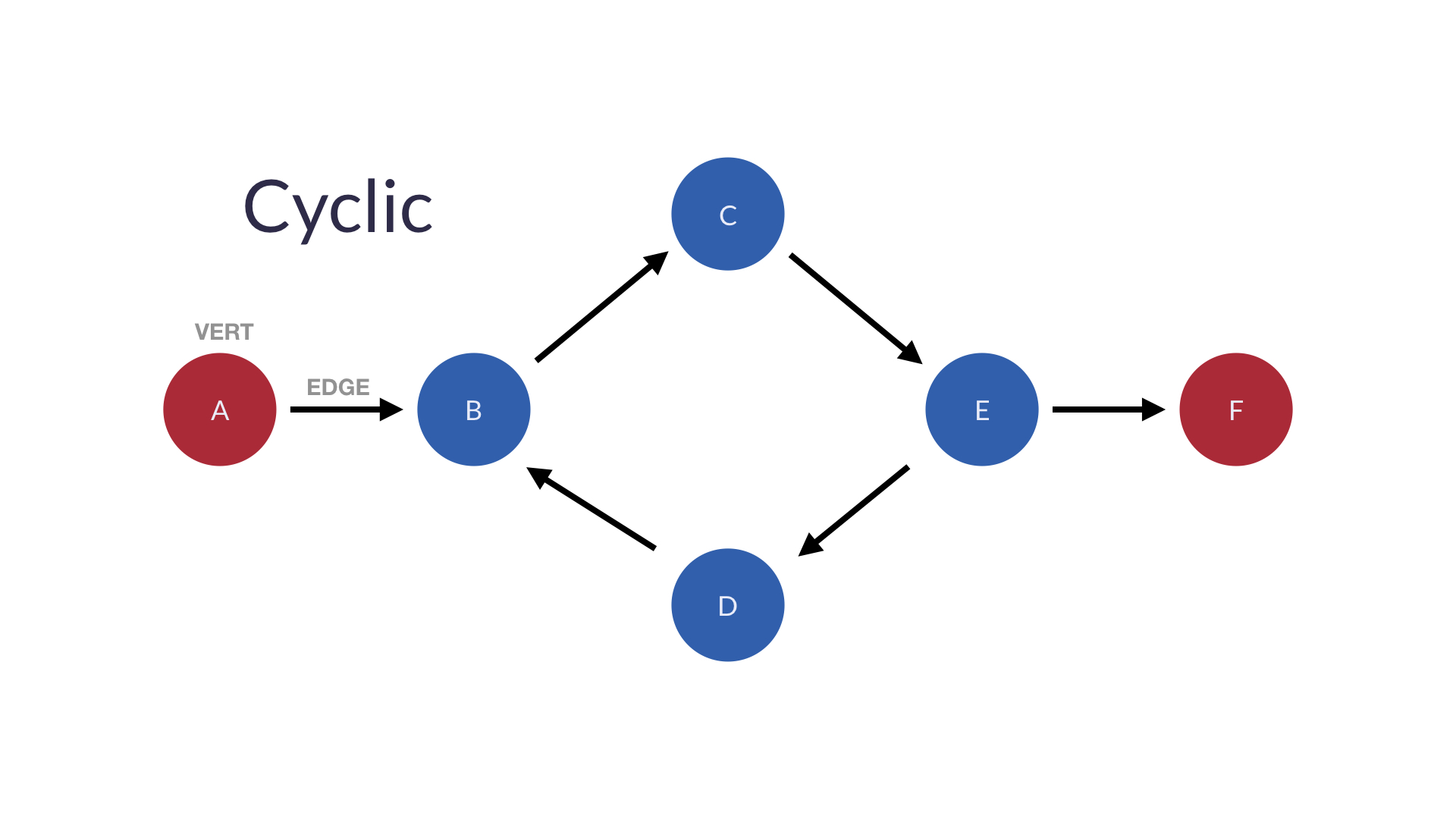
순환성을 가지고 있다면 방문한 노드에 다시 방문하는 루프를 형성할 수 있는 순환 그래프이다.
위의 이미지에서 B에서 시작한 다음 가장자리를 따라 C, E, D로 이동한 다음 이미 방문한 노드인 B로 돌아갈 수 있다.
undirected(무방향성) 그래프는 항상 동일한 노드에 재방문할 수 있으므로 순환 그래프이다.

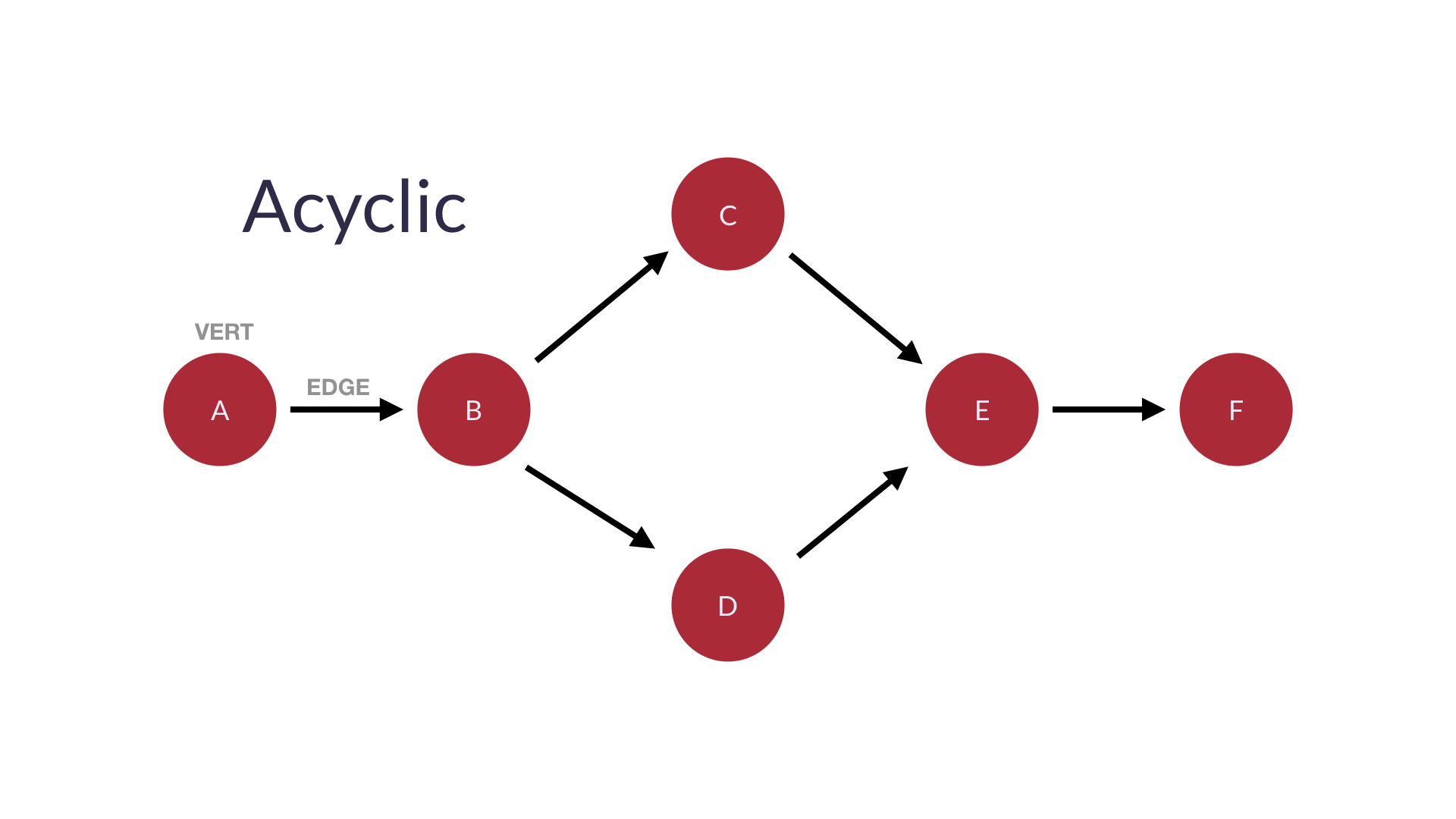
위 그래프처럼 순환을 형성할 수 없는 경우, 비순환 그래프라고 한다.

가중성 vs 비가중성

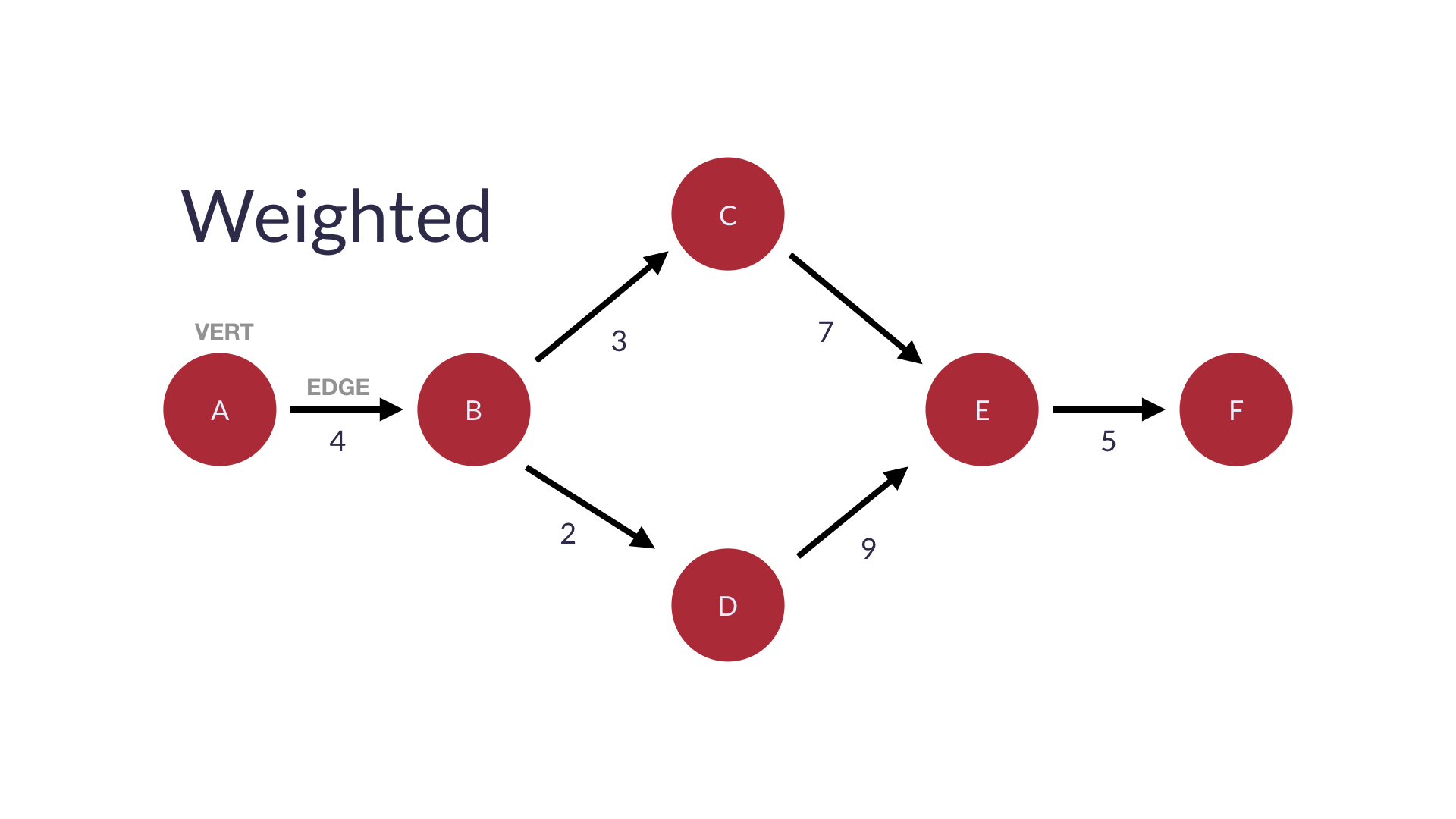
가중 그래프에는 edge(간선)과 관련된 값이 있다.
각 edge의 가중치에 할당된 특정값을 호출한다.
가중치는 서로 다른 그래프에서 서로 다른 데이터를 나타낸다.
예를들어 도로구간을 나타내는 그래프에서 가중치는 도로 길이나 평균 속도 등으로 나타낼 수 있다.
그래프에서 경로의 총 가중치가 높을수록 경로이동시간(비용)이 길어진다.
가중치는 모든 경로 비교 시 어떤 경로를 선택할 지에 사용된다.

순회(traversal)

순회는 그래프에 연결된 노드를 탐색한다.
여기에서 중요한 것은 아직 방문하지 않은 노드의 순회 순서이다.
순회개념은 향후 배우게 되는 DFS, BFS와 같은 순회 알고리즘과 연관되어 있다.

Directed Acyclic Graphs(DAGs)

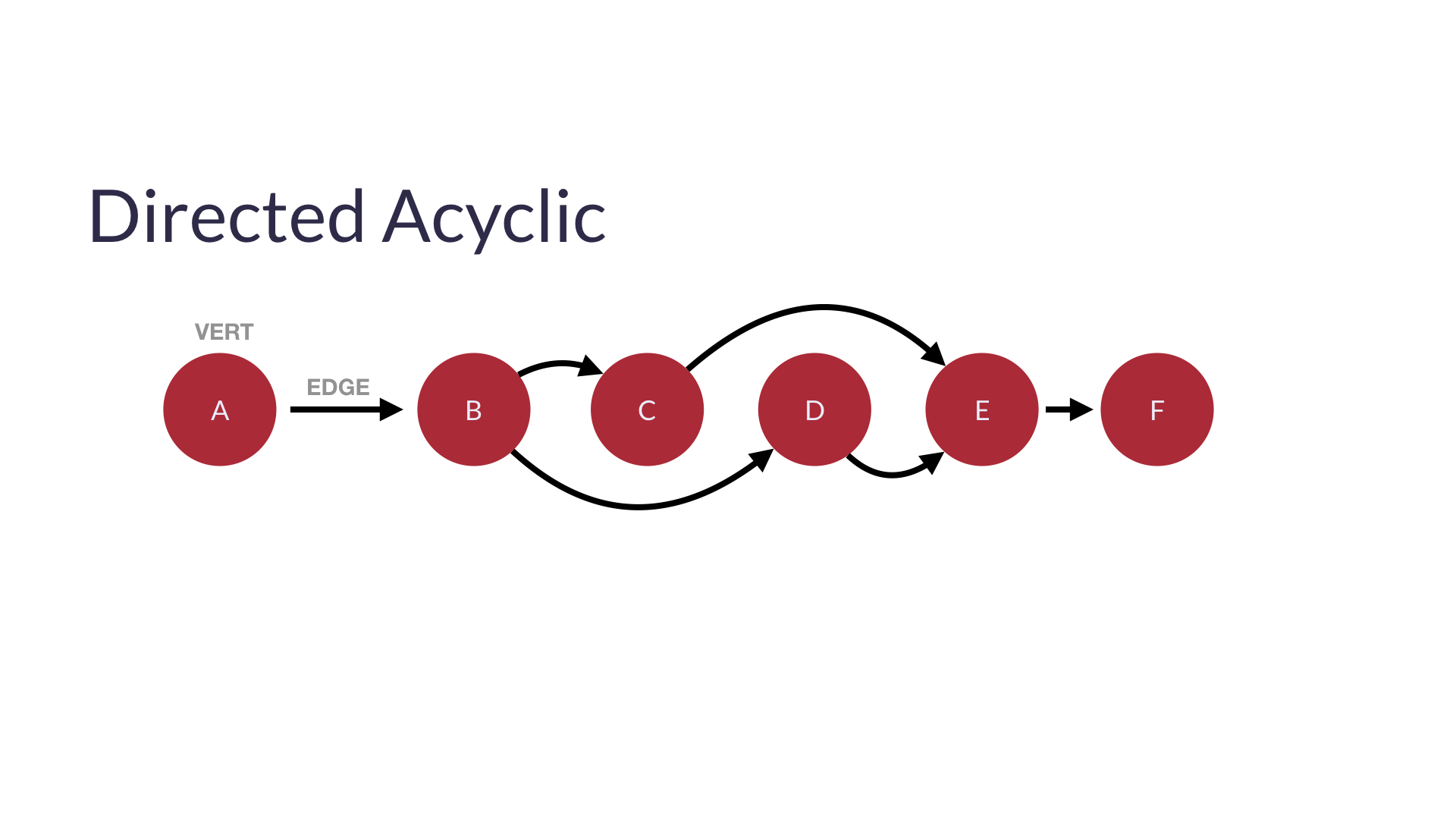
• 방향성 비순환 그래프(Directed Acyclic Graphs)는 순환되지 않는 특정한 단방향 그래프이다.
• 위의 그림처럼 edge가 순서대로 향하도록 DAG의 노드를 선형(단방향)으로 정렬할 수 있다.

그래프의 활용