정수기반 동형암호
-
대칭 키(암호화와 복호화에 같은 키를 사용한다.) 상황
- 비밀키 : p(큰 소수)
- 공개키(연산키) : n = pqi (큰 소수 X 임의의 정수)
- 암호화 : Enc(m) = (m mod p, m mod q) = m + pq
- p 와 q로 각각 나누어도 나머지가 m 인 수
- mod(모듈러) 연산 : 나머지를 구하는 연산 : m mod n == m % n
- 복호화 : Enc(m)(mod p) = ( m + pq )(mod p) = m
-
덧셈과 곱셈에 대해서 동형의 성질을 띈다.
- 덧셈 (단, m1 + m2 < p)
- Enc(m1) + Enc(m2)
= (m1 + pq1) + (m2 + pq2)
= m1 + m2 + p(q1 + q2)
-> 복호화 (mod p) -> m1 + m2 - Enc(m1 + m2)
= m1 + m2 + pq12
-> 복호화 (mod p) -> m1 + m2
- Enc(m1) + Enc(m2)
- 곱셈 (단, m1m2 < p)
- Enc(m1) X Enc(m2)
= (m1 + pq1) X (m2 + pq2)
= m1m2 + m1pq2 + m2pq1 + p2q1q2
-> 복호화 (mod p) -> m1m2 - Enc(m1m2)
= m1m2 + pq12
-> 복호화 (mod p) -> m1m2
- Enc(m1) X Enc(m2)
- 덧셈 (단, m1 + m2 < p)
-
모듈러-2 연산에 대해서 동형의 성질을 띔
-
mod 2 의 덧셈은 XOR 게이트로 구현 가능
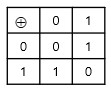
-
mod 2 의 곱셈은 AND 게이트로 구현 가능
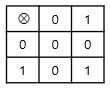
-
모듈러-2 연산을 통하여 AND, OR, NOT 게이트를 구현 가능
- OR : (_XOR_) XOR (_AND_)
- NOT : ( XOR 1)
-
즉, 모든 Boolean Expression이 가능한 Universal Gate가 됩니다.
-
정수기반 동형 암호의 한계
- 81년도에 깨짐.
- 암호문을 반복 사용시, 평문 추측이 가능하다.
- EX-1) 편지 - 특정 구간(~에게, ~드림)의 암호문이 반복된다.
- EX-2) GCD(최대공약수) 문제 - 평문, 암호문 의 쌍이 다수 존재 시, 비밀 키 p 추측 가능
동형 암호의 안전성 - 근사 정수론
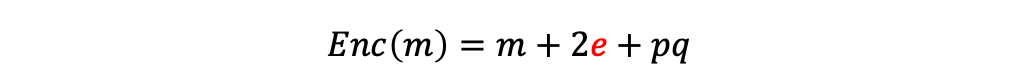
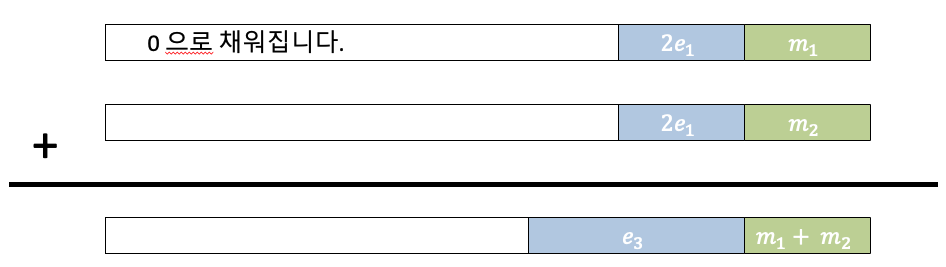
- 메시지의 절반만 사용 및 약간의 노이즈를 추가합니다.
- 반복 사용하여도, 추측이 불가능 하다.
- 덧셈과 곱셈에 대한 동형의 성질이 유지됩니다.
위의 방식으로 만들 수 있는 문제
-
최대공약수 문제

-
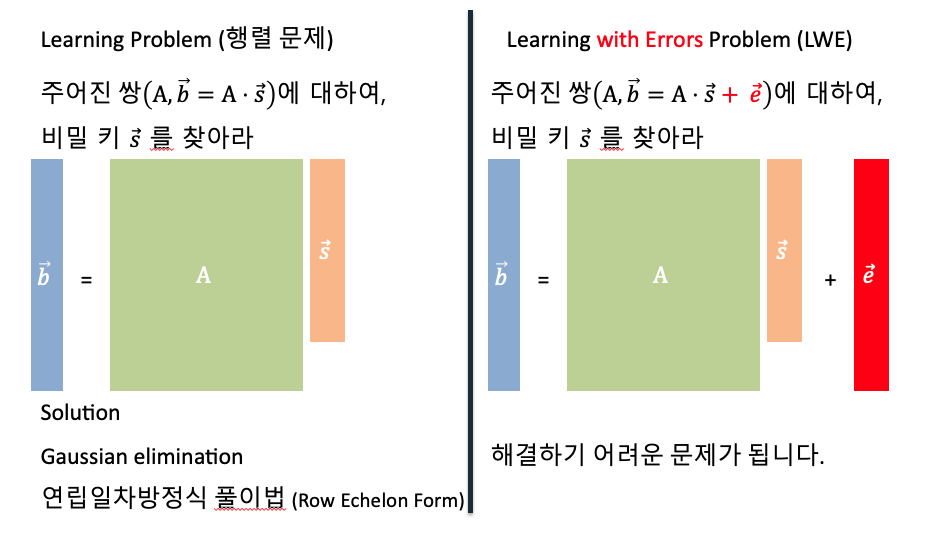
행렬 문제
HEaaN
- 위의 이론을 기반으로 실제 코드 구현 시, 평문 크기가 연산 마다 2배로 증가한다는 문제점 도출
- 해당 문제점을 해결하기 위해, 근사 계산을 지원하는 HEaaN 라이브러리 등장
정의
- Homomorphic Encryption for Arithmetic of Approximate Numbers
- Approximate Numbers
- 어림수, 개수, 근삿값
- 대략적으로 나타낸 수로 올림, 버림, 반올림 등을 하여 얻은 값
- 근삿값 연산을 위한 동형암호
- Approximate Numbers
특징
-
행렬기반 문제를 해결하기 위한 CKKS 스킴 기반
-
근사계산을 지원 (암호화된 정수값의 re-scailing을 지원)
-
항상 같은 크기의 자릿수를 유지할 수 있음?
- 데이터의 일부분을 절삭한다. -
대부분의 응용분야에서는 실수 계산을 필요로 함
(데이터 분석, 기계 학습) -
제공하는 연산 : 더하기, 곱하기, 가위곱
-
기계학습에 많이 쓰임 : 이유 - 데이터를 일부 절삭하여도 가능하기 때문에
