Heap (힙)

힙

정의

• 완전 이진트리의 일종으로 우선순위 큐를 위해 만들어진 자료구조이다.

우선순위 큐 : 우선순위의 개념을 큐에 도입한 자료구조
데이터들이 우선순위를 가지고 있음. 우선순위가 높은 데이터가 먼저 나감

완전 이진트리 : 마지막 레벨을 제외한 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드들이 왼쪽에서부터 차있다.

특징

• 여러 개의 값들 중에서, 최대값과 최소값을 빠르게 찾아내도록 만들어진 자료구조
• 반정렬 상태(느슨한 정렬 상태) 를 유지한다.
  - 큰 값이 상위 레벨에 있고, 작은 값이 하위 레벨에 있다는 정도
  - 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰(작은) 이진 트리를 말한다.
• 힙 트리에서는 중복된 값을 허용한다.

힙의 종류

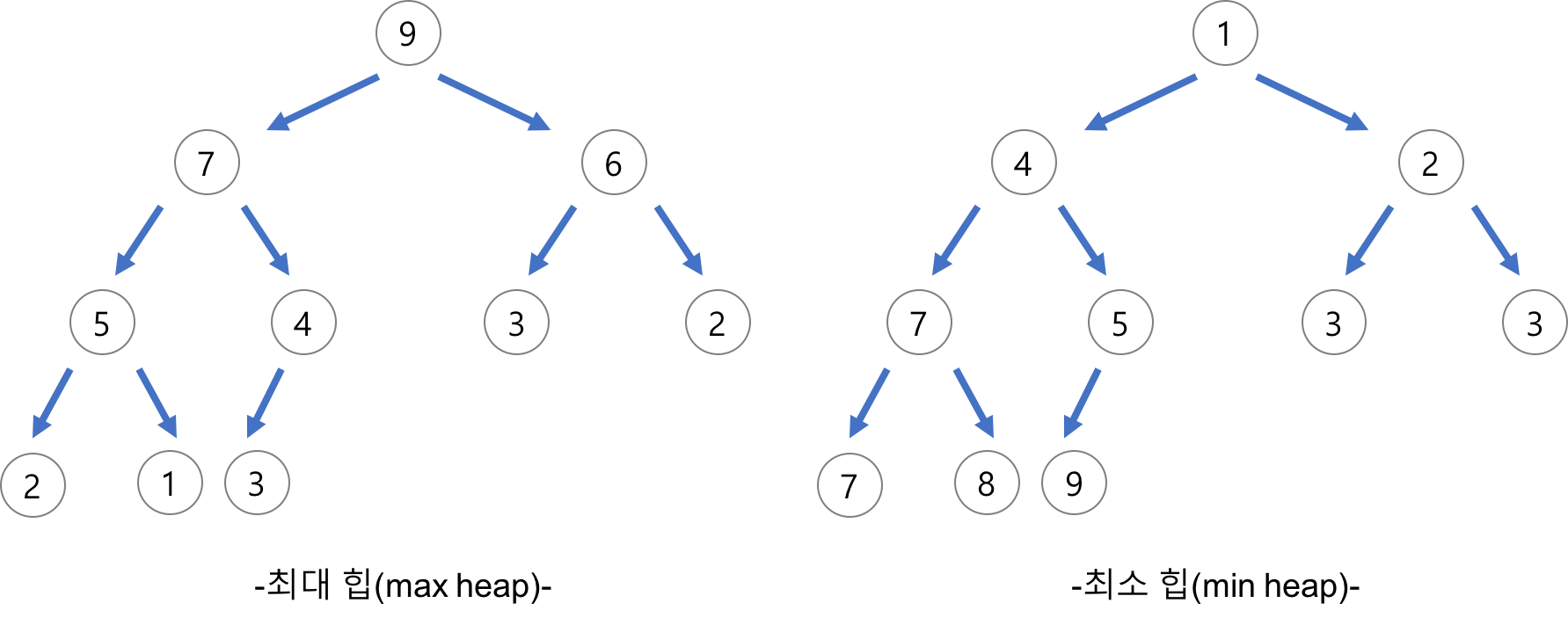
최대 힙(max heap)

• 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
• Key(부모 노드) ≥ Key(자식 노드)

최소 힙(min heap)

• 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
• Key(부모 노드) ≤ Key(자식 노드)

구현

• 힙을 저장하는 표준적인 자료구조는 배열 이다.
• 구현을 쉽게 하기 위하여 배열의 첫 번째 인덱스인 0은 사용되지 않는다.
• 특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않는다.
  - ex) 루트 노드(1) 의 오른쪽 노드 번호는 항상 3 이다.
• 부모 노드와 자식 노드 관계
  - 왼쪽 자식 index = (부모 index) * 2
  - 오른쪽 자식 index = (부모 index) * 2 + 1
  - 부모 index = (자식 index) / 2

기능

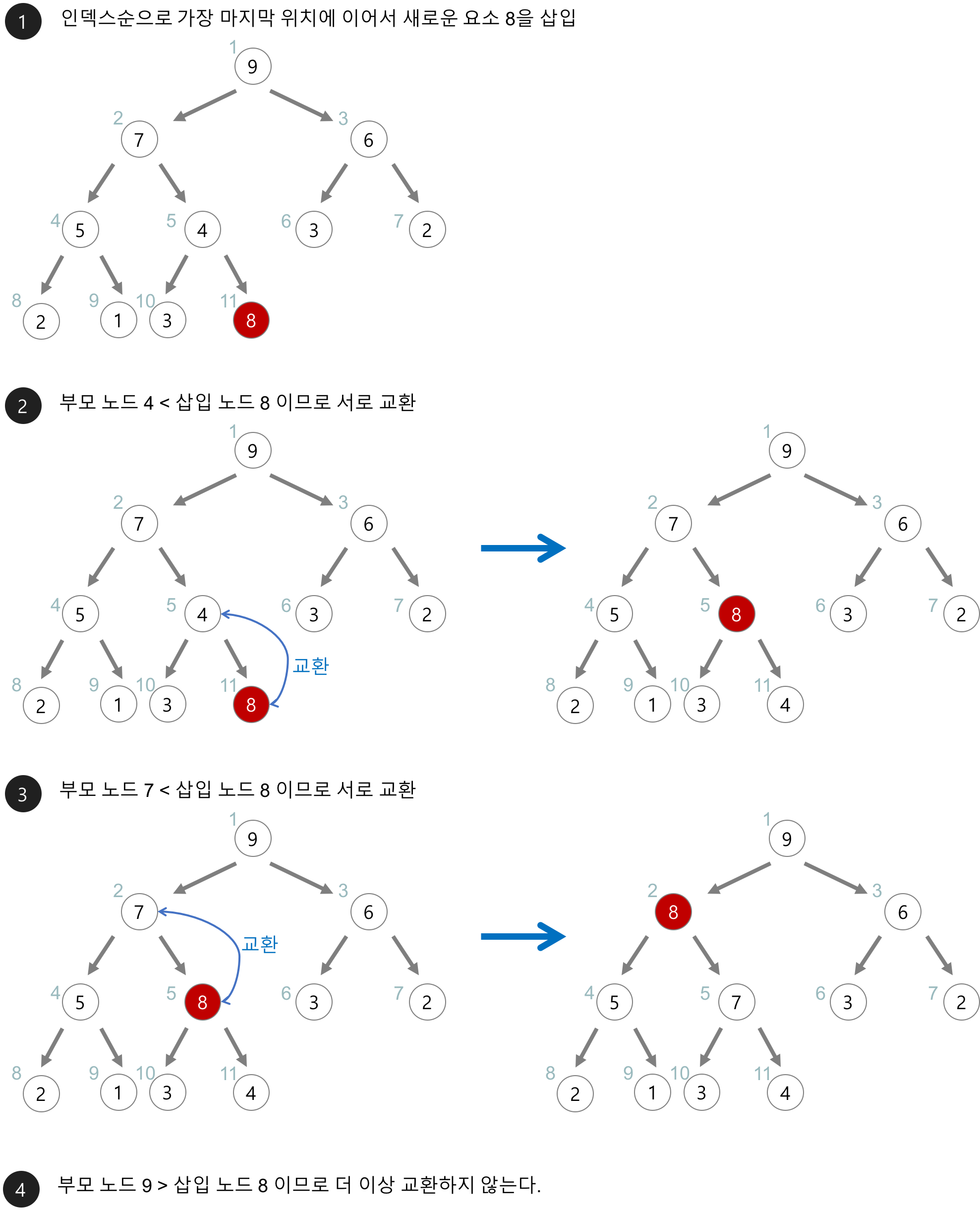
삽입
1. 힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 삽입
2. 새로운 노드를 부모 노드들과 비교하여 교환

• 아래의 최대 힙(max heap)에 새로운 요소 8을 삽입해보자.
  

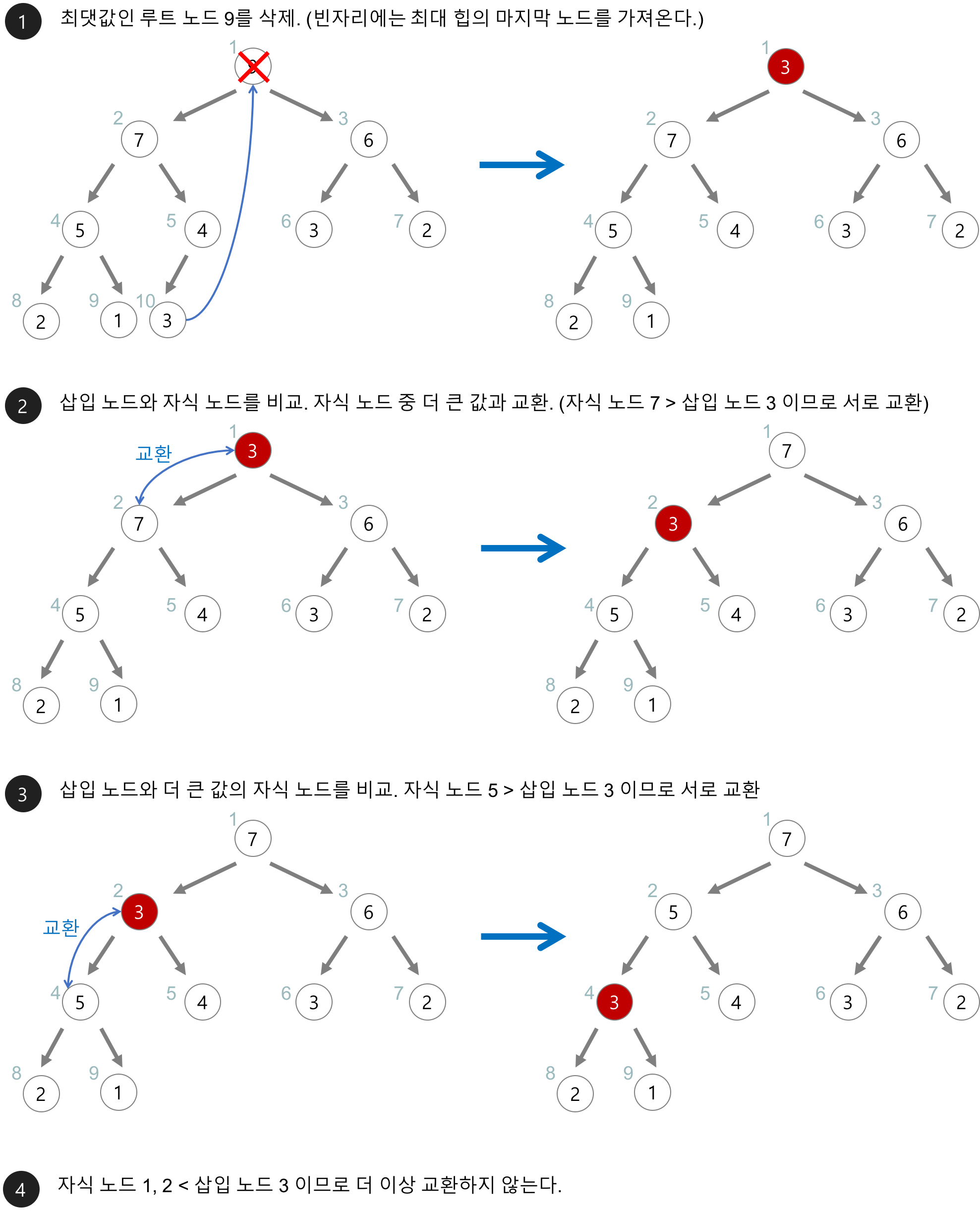
삭제
1. 루트 노드가 삭제됨
2. 삭제된 루트 노드에는 힙의 마지막 노드를 가져옴
3. 힙을 재구성 한다.

• 아래의 최대힙(max heap)에서 최댓값을 삭제해보자.