(일반) 트리
정의
- 노드(데이터)들을 간선으로 연결한 계층형 자료 구조
트리 구조
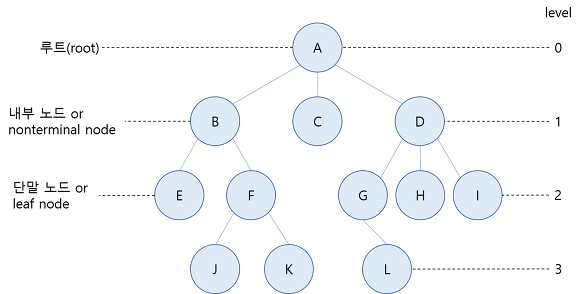
- 트리는 값을 가진 노드(Node) 와 이 노드들을 연결해주는 간선(Edge) 으로 이루어져 있다.
-
root 노드
트리의 가장 위쪽에 있는 노드
루트는 트리에 1개만 존재 -
leaf 노드
= 단말 노드, 외부 노드
자식 노드가 없는 노드
차수가 0인 노드 -
비 단말 노드
= 내부 노드, non-terminal node
리프 노드를 제외한 모든 노드
차수가 1 이상인 노드 -
자식 노드
어떤 노드와 가지로 연결 되었을때 아래쪽 노드 -
부모 노드
어떤 노드와 가지로 연결 되었을때 가장 위쪽 노드 -
형제 노드
부모가 같은 노드 -
서브 트리
어떤 노드를 루트로 하고, 그 자손으로 구성된 트리 -
노드의 차수(degree)
한 노드가 가지고 있는 서브트리의 수
ex) A노드의 차수는 3 이다. (B, C, D) -
트리의 차수(degree of tree)
해당 트리에 있는 노드들의 차수 중에 최대 차수 -
레벨(level)
루트 노드의 level은 0이며, 자식노드로 내려갈 수록 1씩 증가한다 -
노드의 높이
루트에서 해당 노드에 이르는 경로의 길이 즉, 간선의 수 -
트리의 높이
루트에서 가장 멀리 있는 리프까지의 거리
트리의 최대 레벨
트리의 특징
- 트리에는 사이클이 존재할 수 없다. (만약 사이클이 만들어진다면, 그것은 그래프 이다.)
- 모든 노드는 자료형으로 표현이 가능하다.
- 루트에서 한 노드로 가는 경로는 유일한 경로 뿐이다.
- 노드의 개수가 N개면, 간선은 N-1개를 가진다.
트리 순회 방식
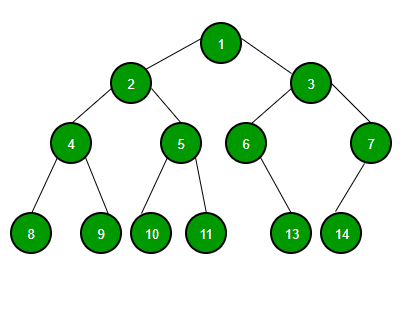
트리를 순회하는 방식은 총 4가지가 있다. 아래의 그림을 예시로 진행해보자
-
1. 너비 우선 검색 (BFS, Breadth First Search)
- 1-1. 레벨 순회(level-order)
루트(Root)부터 계층 별로 방문하는 방식이다.1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 → 9 → 10 → 11 → 12 → 13 → 14
- 1-1. 레벨 순회(level-order)
-
2. 깊이 우선 검색 (DFS, Depth First Search)
리프에 도달할때까지 아래쪽으로 내려가면서 검색하는 것을 우선- 2-1. 전위 순회 (pre-order)
각 루트(Root)를 순차적으로 먼저 방문하는 방식이다.
(Root → 왼쪽 자식 → 오른쪽 자식)1 → 2 → 4 → 8 → 9 → 5 → 10 → 11 → 3 → 6 → 13 → 7 → 14
- 2-2. 중위 순회 (in-order)
왼쪽 하위 트리를 방문 후 루트(Root)를 방문하는 방식이다.
(왼쪽 자식 → Root → 오른쪽 자식)8 → 4 → 9 → 2 → 10 → 5 → 11 → 1 → 6 → 13 → 3 →14 → 7
- 2-3. 후위 순회 (post-order)
왼쪽 하위 트리부터 하위를 모두 방문 후 루트(Root)를 방문하는 방식이다.
(왼쪽 자식 → 오른쪽 자식 → Root)8 → 9 → 4 → 10 → 11 → 5 → 2 → 13 → 6 → 14 → 7 → 3 → 1
- 2-1. 전위 순회 (pre-order)
이진 트리 (binary tree)
정의
- 각각의 노드가 최대 두 개의 자식 노드를 가지는 트리 자료구조
- 자식 노드를 각각 왼쪽 자식 노드 와 오른쪽 자식 노드 라고 한다.
- 다만, 서브트리는 공백이 될 수 있다.
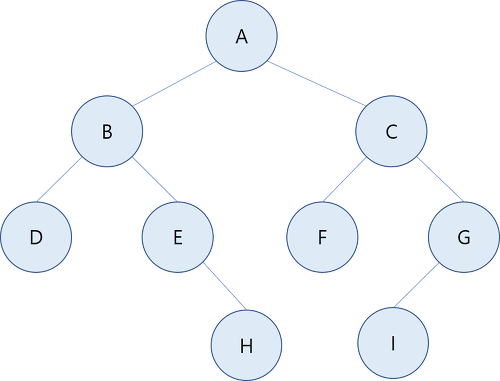
종류
트리 용어는 잘 표준화 되어 있지 않아서 문헌마다 차이가 있다.
-
편향 이진트리(skewed binary tree)
모든 노드가 무보의 왼쪽(or 오른쪽) 자식이기 때문에 왼(or 오른)편으로 편향되어 있다.
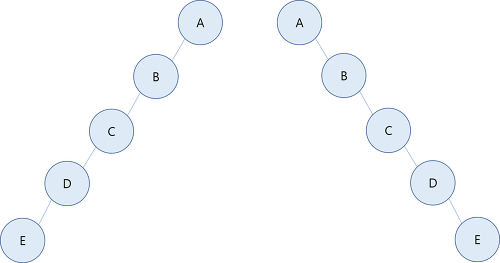
-
포화 이진트리(full binary tree)
이진트리가 보유할 수 있는 최대의 노드를 가지고 있는 형태이다.
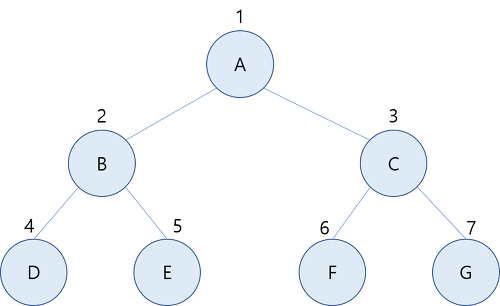
높이가 h인 이진 트리에서 있을 수 있는 최대 노드의 수는 2h+1 이다. -
완전 이진트리(complete binary tree)
마지막 레벨을 제외한 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드들이 왼쪽에서부터 차 있다.
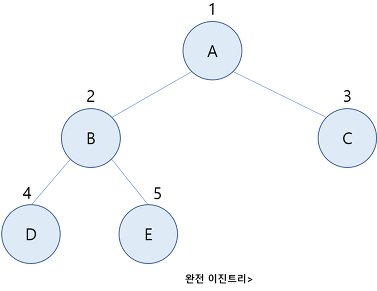

감사합니다