알고리즘 - 정렬(2) 셸 정렬, 퀵 정렬

저번 포스트에 이어 단순 정렬의 비효율적인 시간 복잡도를 개선하기 위한 정렬 방법들을 정리해 보겠다.

목차

1. 버블 정렬
2. 단순 선택 정렬
3. 단순 삽입 정렬
4. 셸 정렬
5. 퀵 정렬
6. 병합 정렬
7. 힙 정렬
8. 도수 정렬

4. 셸 정렬

도널드 L.셸이 고안한 셸 정렬은 단순 삽입 정렬의 장점은 살리고, 단점은 보완하여 더 빠르게 정렬하는 알고리즘이다.

단순 삽입 정렬의 장﹒단점

• 장점 : 이미 정렬을 마쳤거나 정렬이 거의 끝나가는 상태에서는 속도가 아주 빠르다.

• 단점 : 삽입할 위치가 멀리 떨어져 있으면 이동 횟수가 많아진다.

원리

먼저 정렬할 배열의 원소를 그룹으로 나눠 각 그룹별로 정렬을 수행한다. 그 후, 정렬된 그룹을 합치는 작업을 반복하여 원소의 이동 횟수를 줄이는 방법이다.

예를 들면 4, 2, 1 간격 순으로 셸 정렬을 해보자.

우선 0번 인덱스와 4번 인덱스를 한 그룹으로 비교해 교환하고, 마찬가지로 (1, 5), (2, 6), (3, 7)을 비교해 교환하는 작업을 수행한다. (4-정렬)

    						[image source]: https://www.tutorialspoint.com
                            

다시 2만큼 간격의 그룹으로 같은 작업을 반복한다. (2-정렬)

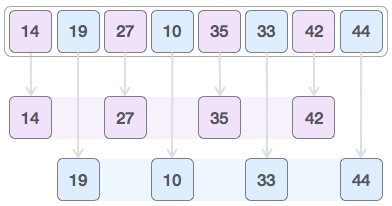
    						[image source]: https://www.tutorialspoint.com

마지막으로 1만큼의 간격으로 같은 작업을 반복하면 정렬이 끝난다. (1-정렬)

    						[image source]: https://www.tutorialspoint.com

셸 정렬의 흐름

• 2개의 원소에서 4-정렬을 수행(4개 그룹, 4번)

• 4개 원소에서 2-정렬을 수행(2개 그룹, 2번)

• 8개 원소에서 1-정렬을 수행(1개 그룹, 1번)

  7번의 정렬은 모두 단순 삽입 정렬
  정렬 횟수는 늘어나지만 전체적으로 원소의 이동 횟수가 줄어들어 효율적이다.

Code

 from typing import MutableSequence
 
 def shell_sort(a: MutableSequence) -> None:
     n = len(a)
     h = n // 2
     while h > 0:
     	for i in range(h, n):
            j = i-h
            tmp = a[i]
            while j >= 0 and a[j] > tmp:
                a[j+h] = a[j]
                j -= h
            a[j+h] = tmp
        h //= 2

h값의 선택

h값이 서로 배수가 되지 않도록 하면, 원소가 충분히 뒤섞이므로 효율 좋은 정렬을 기대할 수 있다.

h = ... -> 121 -> 40 -> 13 -> 4 -> 1 (3n + 1 수열)

하지만 h의 초깃값이 지나치게 크면 효과없다.

따라서 n을 9로 나눈 몫을 넘지 않도록 정해야 한다.

from typing import MutableSequence

def shell_sort(a: MutableSequence) -> None:
    n = len(a)
    h = 1
    
    while h < n // 9:
    	h = h*3 + 1
    while h > 0:
        for i in range(h, n):
           temp = a[i]
           j = i-h
           while j > 0 and a[j] > temp:
               a[j+h] = a[j]
               j -= h
           a[j+h] = temp
        h //= 3

시간 복잡도

셸 정렬의 시간 복잡도는 O(n1.25)이고, 단순정렬의 시간 복잡도인 O(n2)보다 매우 빠르다. 그러나 셸 정렬 알고리즘은 이웃하지 않고 떨어져 있는 원소를 서로 교환하므로 안정적이지 않다.

5. 퀵 정렬(Quick Sort)

퀵정렬은 토니 호어가 고안한 알고리즘으로, 피벗을 기준으로 좌우를 나누는 특징 때문에 파티션 교환 정렬(partition-exchange sort)이라고도 불린다. 병합 정렬과 마찬가지로 분할정복 알고리즘이며 여기에 피벗이라는 개념을 통해 파티셔닝 하면서 쪼개 나간다.
퀵 정렬은 가장 빠른 정렬 알고리즘으로 알려져 있으며 널리 사용되고 있다.

피벗(Pivot)

중심축, 그룹을 나누는 기준. 임의로 선택할 수 있고, 선택된 피벗은 2개로 나눈 그룹 어디에 넣어도 상관 없다.

원리

배열을 두 그룹으로 나누기

먼저 배열을 피벗을 기준으로 두 그룹으로 나눈 후, 피벗을 x, 왼쪽 끝 원소의 인덱스를 pl, 오른쪽 끝 원소의 인덱스를 pr이라 하자. 그룹을 나누려면 피벗 이하인 원소를 배열 왼쪽으로, 피벗 이상인 원소들을 배열 오른쪽으로 이동시켜야 한다.

• a[pl] >= x가 성립하는 원소를 찾을 때까지 pl을 오른쪽 방향으로 스캔
• a[pr] <= x가 성립하는 원소를 찾을 때까지 pr을 왼쪽 방향으로 스캔

이 과정을 거치며 pl과 pr이 각각 피벗 이상인 원소와 피벗 이하인 원소에 위치한다. 여기서 pl과 pr이 위치하는 원소 a[pl]과 a[pr]을 교환한다. 그러면 피벗 이하인 값은 왼쪽으로 이동하고, 피벗 이상인 원소는 오른쪽으로 이동한다.

계속 과정을 반복하다 보면 pl과 pr이 서로 교차하며 그룹 나누는 과정이 끝난다.

• 피벗 이하인 그룹: a[0], ..., a[pl-1]
• 피벗 이상인 그룹: a[pr+1], ..., a[n-1]

그룹을 나누는 작업이 끝난 후 pl > pr+1일 때에 한해 다음과 같은 그룹이 만들어진다.

• 피벗과 일치하는 그룹: a[pr+1], ..., a[pl-1]

pl과 pr이 같은 위치에 있으면 같은 원소를 교환한다. 같은 원소를 교차하지 않으면 원소를 교환할 때마다 매번 pl과 pr이 같은 위치에 있는지 체크해야 하기 때문에, 매번 체크하는 횟수보다 1번만 같은 원소를 교환하는 것이 비용이 적게 든다.

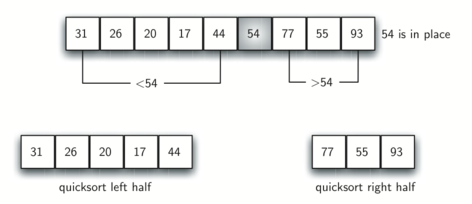
						[image source]: https://www.runestone.academy
                        

원소 수가 1개인 그룹은 더이상 나눌 필요가 없으므로 원소 수가 2개 이상인 그룹만 다음과 같이 반복해서 나눕니다.

• pr가 a[0]보다 오른쪽에 위치하면(left < pr) 왼쪽 그룹을 나눕니다.
• pl이 a[8]보다 왼쪽에 위치하면(pl < right) 오른쪽 그룹을 나눕니다.'

퀵 정렬은 분할 정복 알고리즘이므로 재귀 호출을 사용하여 구현 가능하다.
하지만 퀵 정렬은 서로 이웃하지 않는 원소를 교환하므로 안정적이지 않은 알고리즘이다.

Pseudo Code

QUICK-SORT(A, lo, hi)
    if lo < hi then
        pivot := partition(A, lo, hi)
        QUICK-SORT(A, lo, pivot-1)
        QUICK-SORT(A, pivot+1, hi)

로무토 파티션 함수 Pseudo Code

맨 오른쪽을 피벗으로 정하는 가장 단순한 방식

PARTITION(A, lo, hi)
    pivot := A[hi]
    i := lo
    for j := lo to hi do
        if A[j] < pivot then
            swap A[i] with A[j]
            i := i + 1
        swap A[i] with A[hi]
        return i

로무토 파티션 함수 Code

def partition(lo, hi):
    pivot = A[hi]
    left = lo
    for right in range(lo, hi):
        if A[right] < pivot:
            A[left], A[right] = A[right], A[left]
            left += 1
    A[left], A[hi] = A[right], A[left]
    return left

로무토 파티션 함수를 이용한 퀵 정렬 Code

def quicksort(A, lo, hi):
    def partition(lo, hi):
        pivot = A[hi]
        left = lo
        for right in range(lo, hi):
            if A[right] < pivot:
                A[left], A[right] = A[right], A[left]
                left += 1
        A[left], A[hi] = A[right], A[left]
        return left
        
    if lo < hi:
    pivot = partition(lo, hi)
    quicksort(A, lo, pivot-1)
    quicksort(A, pivot+1, hi)

Code

피벗을 가운데 위치시켜 퀵 정렬 만들기

from typing import MutableSequence

def q_sort(a: MutableSequence, left: int, right: int) -> None:
    pl = left
    pr = right
    x = a[(pl+pr) // 2]
    while pl <= pr:
        while a[pl] < x:
            pl += 1
        while a[pr] > x:
            pr -= 1
        if pl <= pr:
            a[pl], a[pr] = a[pr], a[pl]
            pl += 1
            pr -= 1
            
    if left < pr:
        q_sort(a, left, pr)
    if pl < right:
        q_sort(a, pl, right)
        
 def quick_sort(a: MutableSequence) -> None:
     q_sort(a, 0, len(a)-1)

비재귀적 퀵 정렬

from stack import Stack
from typing import MutableSequence

def q_sort(a: MutableSequence, left: int, right: int) -> None:
    range = Stack(right - left +1)
    
    range.push((left, right))
    
    while not range.is_empty():
        pl, pr = left, right = range.pop()
        x = a[(left+right) // 2]
        
        while pl <= pr:
            while a[pl] < x: pl += 1
            while a[pr] > x: pr -= 1
            if pl <= pr:
                a[pl], a[pr] = a[pr], a[pl]
                pl += 1
                pr -= 1
                
        if left < pr: range.push((left, pr))
        if pl < right: range.push((pl, right))

데이터를 임시 저장하기 위해 다음 스택을 사용함

• range: 나눌 범위에서 맨 앞 원소의 인덱스와 맨 끝 원소의 인덱스를 조합한 튜플 스택

스택의 크기는 right-left+1이며 나누는 배열의 원소 수와 같다.

튜플로 나눠야 할 배열의 범위를 넣어줌

스택이 비어있다면 나눠야할 배열이 없다는 것이므로 종료

스택의 크기

스택의 크기는 정렬 대상인 배열의 원소 수와 같은 값으로 한다.
적당한 스택의 크기는?

• 규칙 1: 원소 수가 많은 쪽의 그룸을 먼저 푸시한다.
• 규칙 2: 원소 수가 적은 쪽의 그룹을 먼저 푸시한다.

일반적으로 원소 수가 적은 배열일수록 나누는 과정을 빠르게 마칠 수 있다. 따라서 규칙 1과 같이 원소 수가 많은 그룹의 나누기를 나중에 하고, 원소 수가 적은 그룹의 나누기를 먼저 하면 스택에 동시에 쌓이는 데이터의 개수가 적어진다.

규칙 1, 2의 경우 스택에 넣고 꺼내는 횟수는 같지만, 동시에 쌓이는 데이터의 최대 개수가 다르다.

규칙 1에서 배열의 원소 수가 n이면, 스택에 쌓이는 데이터의 최대 개수는 log n보다 적다. 따라서 원소 수 n이 100만 개라도 스택의 최대 크기는 20으로 충분하다.

피벗 선택하기

피벗 서택 방법은 퀵 정렬의 실행효율에 큰 영향을 미친다. 한쪽으로 치우친 분할을 반복하면 빠른 정렬 속도를 기대할 수 없다. 빠른 정렬을 하려면 배열을 정렬한 뒤 가운데에 위치하는 값, 중앙값을 피벗으로 하는 게 이상적이다. 하지만 중앙값을 구하려면 그에 대한 처리가 필요하고, 이를 위해 많은 시간이 걸려 피벗을 선택하는 의미가 없어진다.

다음 방법을 사용하면 최악의 경우를 피할 수 있다.

• 방법 1: 나누어야 할 배열의 원소 수가 3 이상이면, 배열에서 임의의 원소 3개를 꺼내 중앙값인 원소를 피벗으로 선택

• 방법 2: 나누어야 할 배열의 맨 앞 원소, 가운데 원소, 맨 끝 원소를 정렬한 뒤 가운데 원소와 맨 끝에서 두 번째 원소를 교환한다. 맨 끝에서 두 번째 원솟값 a[right-1]를 피벗으로 선택하고, 동시에 나눌 대상을 a[left+1] ~ a[right-2]로 좁힌다.

방법 2의 과정을 거치고 나면 스캔할 커서의 위치를 다음과 같이 변경할 수 있다.

• 왼쪽 커서 pl의 시작 위치: left -> left+1
• 오른쪽 커서 pr의 시작 위치: right -> right-2

이 방법을 사용하면 나누는 그룹이 한쪽으로 치우치는 것을 피할 수 있고, 스캔할 원소 3개를 줄일 수 있다.

시간 복잡도

퀵 정렬은 배열을 조금씩 나누어 보다 작은 문제를 푸는 과정을 반복하므로 시간 복잡도는 O(n log n)이다. 그런데 정렬하는 배열의 초깃값이나 피벗을 선택하는 방법에 따라 증가하는 경우도 있다. 최악의 경우는 O(n2)이 된다. 이미 정렬된 정렬이 입력값으로 드러왔다면 파티셔닝이 이루어지지 않고 결국 전체를 비교하기 때문에, 버블 정렬과 다를 바 없는 최악의 성능을 보이게 된다.

퀵 정렬은 원소 수가 적은 경우에는 그다지 빠른 알고리즘이 아니다.
따라서 다음과 같이 구현할 수도 있다.

• 원소 수가 9개 미만인 경우 단순 삽입 정렬로 전환
• 피벗 선택은 방법 2를 채택

 from typing import MutableSequence
 
 def sort3(a: MutableSequence, idx1: int, idx2: int, idx3: int):
     if a[idx2] < a[idx1]: a[idx1], a[idx2] = a[idx2], a[idx1]
     if a[idx3] < a[idx2]: a[idx2], a[idx3] = a[idx3], a[idx2]
     if a[idx2] < a[idx1]: a[idx1], a[idx2] = a[idx2], a[idx1]
     return idx2
     
 def insertion_sort(a: MutableSequence, left: int, right: int) -> None:
     for i in range(left+1, right+1)
         j = i
         tmp = a[i]
         while j > 0 and a[j-1] > tmp:
            a[j] = a[j-1]
            j -= 1
         a[j] = tmp
         
 def qsort(a: MutableSequence, left: int, right: int) -> None:
     if right-left < 9:
         insertion_sort(a, left, right)
     else:
         pl = left
         pr = right
		 m = sort3(a, pl, (pl+pr) // 2, pr)
         x = a[m]
         
         a[m], a[pr-1] = a[pr-1], a[m]
         pl += 1
         pr -= 2
         while pl < pr:
             while a[pl] < x: pl += 1
             while a[pr] > x: pr -= 1
             if pl <= pr:
                 a[pl], a[pr] = a[pr], a[pl]
                 pl += 1
                 pr -= 1
             
         if left < pr: qsort(a, left, pr)
         if pl < right: qsort(a, pl, right)
         
 def quick_sort(a: MutableSequence) -> None:
     qsort(a, 0, len(a)-1)

퀵 정렬은 불안정 정렬인데다 입력값에 따라 버블 정렬 만큼이나 느려질 수 있다. 최고의 알고리즘이라 칭송받던 퀵 정렬이 경우에 따라서는 최악의 알고리즘이 될 수도 있다. 이처럼 고르지 않은 성능 탓에 실무에서는 병합 정렬이 여전히 활발히 쓰이고 있으며, 파이썬의 기본 정렬 알고리즘으로는 병합 정렬과 삽입 정렬을 휴리스틱하게 조합한 팀소트(Timsort)를 사용한다.