깊이 우선 탐색(DFS)

• 특정 정점에서 시작해서 트리나 그래프에서 한가지 경로를 최대한 깊게 탐색하고, 해당 경로를 끝까지 탐색한 후 다른 경로로 이동
• 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가, 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 다른 방향으로 다시 탐색을 진행하는 방법과 유사
• 모든 정점을 방문하고자 하는 경우에 사용

• 일반적으로 재귀 함수를 사용하여 구현
  Stack으로도 구현 가능
• 모든 경우의 수에 대해 탐색을 진행
• 사이클이 있는 경우, 무한 루프에 빠지지 않도록 방문 체크를 해주어야 함
• BFS보다 깊은 경로를 빠르게 찾는데 용이

진행 순서

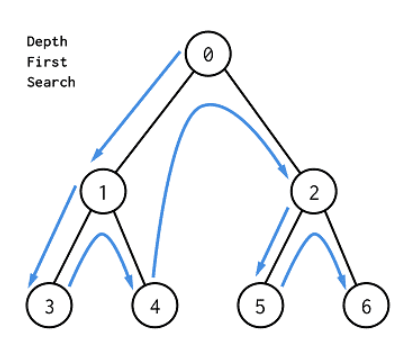
• 한 방향으로 갈 수 있을 때까지 계속 가다가, 더 이상 갈 수 없게 되면 다시 가장 가까운 분기점으로 돌아와서 다른 방향으로 다시 탐색을 진행

시간 복잡도

• V -> 노드의 수, E -> 간선의 수
• 인접 리스트로 표현된 그래프 : O(V+E)
• 인접 행렬로 표현된 그래프 : O(V^2)
• 그래프 내에 적은 숫자의 간선만 가지는 그래프는 인접 행렬보다 인접 리스트를 사용하는 것이 유리

예시 코드

public class DFSGraph {
    // 그래프를 인접 리스트로 표현
    static List<List<Integer>> graph = new ArrayList<>();
    static boolean[] visited; // 방문 여부를 체크하는 배열

    public static void main(String[] args) {
        // 1. 그래프 초기화 (1-based indexing)
        int numberOfNodes = 10; // 노드의 개수
        visited = new boolean[numberOfNodes + 1]; // 방문 배열

        // 인접 리스트 초기화
        for (int i = 0; i <= numberOfNodes; i++) {
            graph.add(new ArrayList<>());
        }

        // 2. 그래프에 간선 추가 (주어진 트리 구조에 맞게 연결)
        addEdge(1, 2);
        addEdge(1, 5);
        addEdge(1, 9);
        addEdge(2, 3);
        addEdge(3, 4);
        addEdge(5, 6);
        addEdge(5, 8);
        addEdge(6, 7);
        addEdge(9, 10);

        // 3. DFS 탐색 시작
        System.out.println("DFS 탐색 결과:");
        dfs(1); // 시작(root - 1번) 노드부터 탐색 시작
    }

    // 간선을 추가하는 메서드
    static void addEdge(int from, int to) {
        graph.get(from).add(to); // 방향 그래프가 아니라 무방향 그래프라면
        graph.get(to).add(from); // 무방향 그래프이므로 양방향 간선 추가 (필요한 경우)
    }

    // DFS 알고리즘 구현 메서드
    static void dfs(int now) {
        visited[now] = true; // 현재 노드를 방문 처리
        System.out.print(now + " "); // 방문한(현재) 노드 출력

        // 현재 노드에 연결된 다음 노드를 재귀적으로 방문
        for (int next : graph.get(now)) {
            if (!visited[next]) { // 방문하지 않은 노드라면
                dfs(next);        // 재귀 호출
            }
        }
    }
}

너비 우선 탐색(BFS)

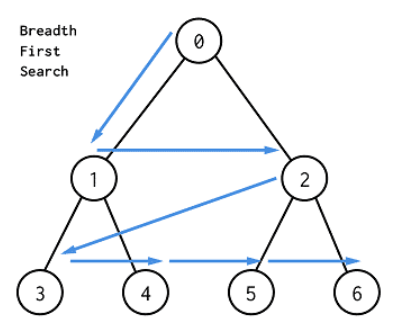
• 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것
• 루트 노드에서 시작해서 인접한 노드를 먼저 탐색하는 방법
• 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 사용
• 재귀적으로 동작하는 DFS와 달리 BFS는 주로 큐를 사용
• 물 웅덩이에 돌멩이를 하나 던지면, 파동이 전체 방향으로 퍼져나가는 동심원이 형태로 탐색이 진행

시간 복잡도

• V -> 노드의 수, E -> 간선의 수
• 인접 리스트로 표현된 그래프 : O(V+E)
• 인접 행렬로 표현된 그래프 : O(V^2)

• 두 방식 모두 조건 내의 모든 노드를 검색한다는 점에서 시간 복잡도는 동일하지만 일반적으로 DFS를 재귀함수로 구현한다는 점에서 DFS보다 BFS가 조금 더 빠르게 동작
• 주어딘 그래프의 구조와 싲가 노드에 따라서 실제 시간 복잡도가 다를 수 있으며 어떤 알고리즘이 더 효율적인지는 그래프의 형태와 알고리즘의 목적에 따라 달라짐 일반적으로 어떤 알고리즘을 선택할지는 문제의 특성과 요구 사항에 따라 결정

공통점

• 그래프에서 시작된 노드로부터 목적지 노드까지 도달하거나 특정 정보를 찾는 것이 목표
• 방문 기록을 체크함으로써, 이미 방문한 노드를 다시 방문하지 않게 하여 무한 루프 방지

차이점

• DFS는 주로 재귀로 구현하지만, BFS는 큐 자료구조를 활용하여 구현
• 동작 순서 상 DFS는 트리를 탐색할 때 주로 사용, BFS는 최단 경로 탐색에 자주 사용

예시 코드

package org.example.p147;

// 문제: 너비 우선 탐색(BFS)을 사용하여 그래프 탐색 (인접 행렬 사용)
// 인접 행렬로 표현된 그래프: 𝑂(𝑉^2)

import java.util.*;

public class BFSMatrix {
    // 그래프를 인접 행렬로 표현
    static int[][] graph;
    static boolean[] visited; // 방문 여부를 체크하는 배열

    public static void main(String[] args) {
        // 1. 그래프 초기화 (1-based indexing)
        int numberOfNodes = 10; // 노드의 개수
        graph = new int[numberOfNodes + 1][numberOfNodes + 1]; // 인접 행렬 생성
        visited = new boolean[numberOfNodes + 1]; // 방문 배열

        // 2. 그래프에 간선 추가 (주어진 트리 구조에 맞게 연결)
        addEdge(1, 2);
        addEdge(1, 3);
        addEdge(1, 4);
        addEdge(2, 5);
        addEdge(3, 6);
        addEdge(3, 7);
        addEdge(4, 8);
        addEdge(5, 9);
        addEdge(6, 10);

        // 3. BFS 탐색 시작
        System.out.println("BFS 결과:");
        bfs(1); // 시작 노드부터 탐색 시작
    }

    // 간선을 추가하는 메서드
    static void addEdge(int from, int to) {
        graph[from][to] = 1; // 방향 그래프라면 한쪽만
        graph[to][from] = 1; // 무방향 그래프의 경우 양쪽을 추가
    }

    // BFS 메서드
    static void bfs(int start) {
        Queue<Integer> queue = new LinkedList<>(); // BFS를 위한 큐 생성
        queue.add(start); // 시작 노드를 큐에 추가
        visited[start] = true; // 시작 노드를 방문 처리

        while (!queue.isEmpty()) {
            int now = queue.poll(); // 큐에서 현재 노드 꺼내기
            System.out.print(now + " "); // 방문한 노드 출력

            // 현재 노드에 연결된 다음 노드를 큐에 추가
            for (int i = 1; i < graph.length; i++) { // 인접 행렬을 순회
                if (graph[now][i] == 1 && !visited[i]) { // 간선이 존재하고 방문하지 않은 경우
                    visited[i] = true;
                    queue.add(i);
                }
            }
        }
    }
}

EX) 미로 찾기
N×M 크기의 미로가 있다.
1행 1열을 나타내는 (1,1)에서 시작하여 (N,M)까지 이동해야 미로를 탈출할 수 있다.
이때, 미로의 좌측 최상단이 (1,1)이다.
또한, 한 칸에서 다른 칸으로 이동할 때, 상하좌우로 서로 인접한 칸으로만 이동할 수 있으며 1초가 걸린다.
N, M 그리고 미로의 정보가 주어질 때, 미로를 탈출하기 위해서는 최소 몇 초가 필요한 지 알려주는 프로그램을 작성해 보세요.

정답 코드

import java.io.*;
import java.util.*;

class Main {
    private static boolean[][] visit;
    private static int[][] raze;
    private static int cnt = 0;
    private static int[] dx = {-1, 0, 1, 0};
    private static int[] dy = {0, 1, 0 ,-1};
    private static int N;
    private static int M;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        String s = br.readLine();
        String[] ss = s.split(" ");
        
        N = Integer.parseInt(ss[0]);    
        M = Integer.parseInt(ss[1]); 

        visit = new boolean[N][M];   
        raze = new int[N][M];

        for(int i=0; i<N; i++){
            String s2 = br.readLine();
            String[] ss2 = s2.split(" ");
            for(int j=0; j<M; j++){
                raze[i][j] = Integer.parseInt(ss2[j]);
            }
        }

        visit[0][0] = true;
        bfs(0, 0);

        if(raze[N-1][M-1] == 1) {
            System.out.println(-1);
        } else { 
            System.out.println(raze[N-1][M-1]-1);
        }
        

    }

    public static void bfs(int x, int y) {
        Queue<int[]> q = new LinkedList<>();
        q.add(new int[] {x, y});

        while(!q.isEmpty()){
            int[] now = q.poll();
            int nowX = now[0];
            int nowY = now[1];

            for(int i=0; i<4; i++){
                int nextX = nowX + dx[i];
                int nextY = nowY + dy[i];

                if(nextX<0 || nextX>=N || nextY<0 || nextY>=M){
                    continue;
                }

                if(raze[nextX][nextY]==0 || visit[nextX][nextY]){
                    continue;
                }

                q.add(new int[] {nextX, nextY});
                raze[nextX][nextY] = raze[nowX][nowY] + 1;
                visit[nextX][nextY] = true;
            }
        }

        
    }

}

컴포넌트 구하기

import java.io.*;
import java.util.*;

class Main {
    private static boolean[] visit;
    private static ArrayList<ArrayList<Integer>> graph = new ArrayList<>();

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        String s = br.readLine();
        String[] ss = s.split(" ");

        int N = Integer.parseInt(ss[0]);
        int M = Integer.parseInt(ss[1]);

        visit = new boolean[N + 1];
        for (int i = 0; i < N + 1; i++) {
            graph.add(new ArrayList<>());
        }

        for (int i = 0; i < M; i++) {
            String s2 = br.readLine();
            String[] ss2 = s2.split(" ");

            int start = Integer.parseInt(ss2[0]);
            int end = Integer.parseInt(ss2[1]);

            addEdge(start, end);
        }

        int cnt = 0;
        for (int i = 1; i <= N; i++) {
            if (!visit[i]) {
                cnt++;
                bfs(i);
            }
        }

        System.out.print(cnt);
    }

    public static void addEdge(int start, int end) {
        graph.get(start).add(end);
        graph.get(end).add(start);
    }

    public static void bfs(int start) {
        Queue<Integer> queue = new LinkedList<>();
        queue.add(start);
        visit[start] = true;

        while (!queue.isEmpty()) {
            int current = queue.poll();

            for (int neighbor : graph.get(current)) {
                if (!visit[neighbor]) {
                    visit[neighbor] = true;
                    queue.add(neighbor);
                }
            }
        }
    }
}