CCW (Counter Clockwise)

CCW (Counter Clockwise) : 세 점의 방향성 판별

CCW 알고리즘이란?

2차원 평면에 존재하는 3개의 점에 대해 나올 수 있는 방향성
- 방향성 종류: 시계 방향, 반시계 방향, 일직선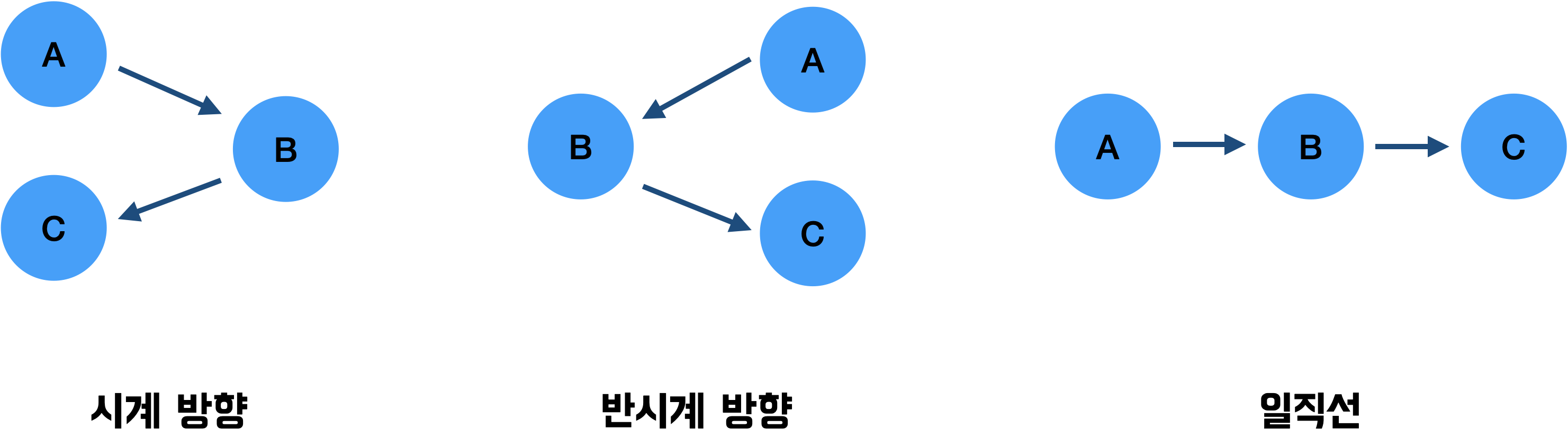

1. 외적

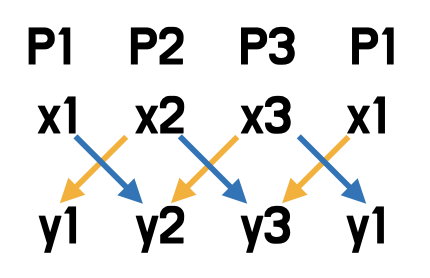
2차원 평면 상에 3개의 점 P1(x1, y1), P2(x2, y2), P3(x3, y3) 이 있을 때, 외적값(CP)은?

CP = (x1*y2 + x2*y3 + x3*y1) - (x2*y1 + x3*y2 + x1*y3)

[ 신발끈 공식을 활용 ]

• 파랑색(+), 노랑색(-) 부분

2. 결과값

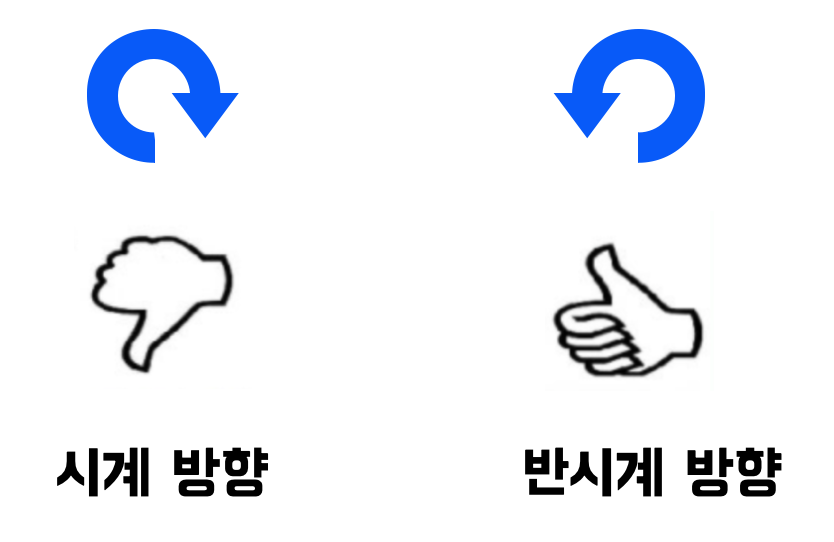
오른손 법칙 적용 (엄지의 방향)

• CP < 0 : 세 점 P1, P2, P3이 시계 방향
• CP > 0 : 세 점 P1, P2, P3이 반시계 방향
• CP = 0 : 세 점 P1, P2, P3이 일직선

3. CCW 알고리즘 코드

int ccw(pair<ll, ll> p1, pair<ll, ll> p2, pair<ll, ll> p3) {
    ll tmp = (p2.first * p3.second + p3.first * p1.second + p1.first * p2.second) - (p3.first * p2.second + p1.first * p3.second + p2.first * p1.second);
    
    if(tmp < 0) return -1;			/* 시계 방향 */
    else if (tmp == 0) return 0;	/* 일직선 */
    else return 1;					/* 반시계 방향 */
}

---

두 선분의 교차 판단

1. 세 점이 일직선 위에 있는 경우가 없을 때

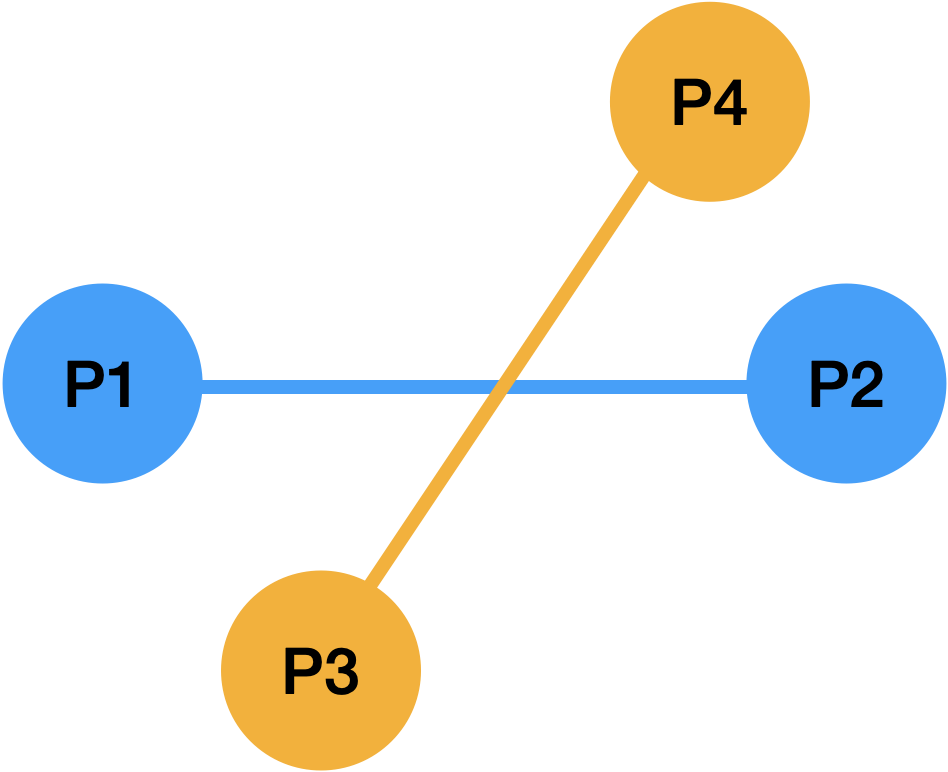
선분 P1-P2 를 기준으로 세 점 P1, P2, P3 과 세 점 P1, P2, P4 에 대해서 각각 CCW 알고리즘을 적용

P1 -> P2 -> P3: 시계 방향 (-1)
P1 -> P2 -> P4: 반시계 방향 (+1)

2. 세 점이 일직선 위에 있는 경우

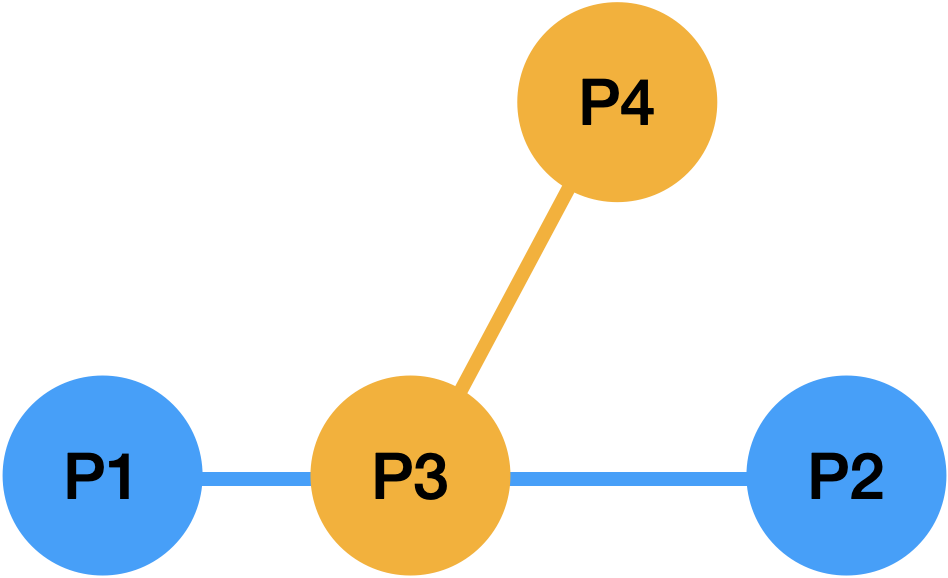
선분 P1-P2 를 기준으로 세 점 P1, P2, P3 과 세 점 P1, P2, P4 에 대해서 각각 CCW 알고리즘을 적용

P1 -> P2 -> P3: 일직선 (0)
P1 -> P2 -> P4: 반시계 방향 (+1)

3. 결과

CCW(P1, P2, P3) * CCW(P1, P2, P4) <= 0 일 때, 두 선분이 교차함

하지만, 이 식에는 반례가 존재 !!

[반례 1]

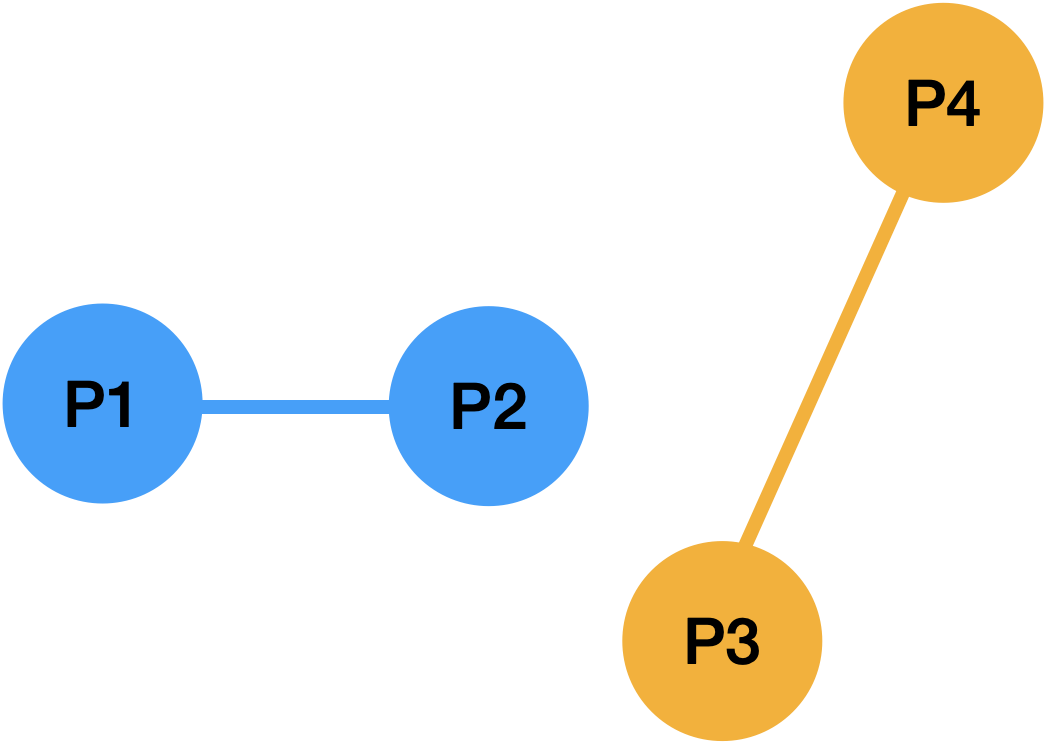
선분 P1-P2 를 기준으로 세 점 P1, P2, P3 과 세 점 P1, P2, P4 에 대해서 각각 CCW 알고리즘을 적용

P1 -> P2 -> P3: 시계 방향 (-1)
P1 -> P2 -> P4: 반시계 방향 (+1)

CCW(P1, P2, P3) * CCW(P1, P2, P4) <= 0 수식에 성립하지만, 두 선분이 교차하지 않음을 알 수 있음

그럼 선분 P1-P2 이 아닌, 선분 P3-P4 를 기준으로 CCW 알고리즘을 적용하면 어떻게 될까?

P3 -> P4 -> P1: 반시계 방향 (+1)
P3 -> P4 -> P2: 반시계 방향 (+1)

CCW(P3, P4, P1) * CCW(P3, P4, P2) <= 0 수식이 성립하지 않음!!

결과적으로 선분 P1-P2 를 기준으로 CCW 알고리즘을 적용한 값과 선분 P3-P4 를 기준으로 CCW 알고리즘을 적용한 값 모두 0 이하일 때, 두 선분이 교차한다고 할 수 있음

[반례 1]을 해결한 결과

(CCW(P1, P2, P3) * CCW(P1, P2, P4) <= 0) && (CCW(P3, P4, P1) * CCW(P3, P4, P2) <= 0)

[반례 2]

선분 P1-P2 를 기준으로 세 점 P1, P2, P3 과 세 점 P1, P2, P4 에 대해서 각각 CCW 알고리즘을 적용

P1 -> P2 -> P3: 일직선 (0)
P1 -> P2 -> P4: 일직선 (0)

CCW(P1, P2, P3) * CCW(P1, P2, P4) <= 0 수식에 성립하지만, 두 선분이 교차하지 않음을 알 수 있음

따라서, 모든 점이 일직선 상에 존재할 때(CCW 알고리즘 값이 모두 0인 경우) 에는 아래 그림처럼 두 선분이 서로 포개져 있는지 확인하는 부분이 필요함

[반례 2]을 해결하기 위한 조건

(P3 <= P2) && (P1 <= P4)

4. 최종 코드

bool isCross(pair<ll, ll> s1, pair<ll, ll> e1, pair<ll, ll> s2, pair<ll, ll> e2) {
    int s1e1 = ccw(s1, e1, s2) * ccw(s1, e1, e2);
    int s2e2 = ccw(s2, e2, s1) * ccw(s2, e2, e1);

    if(s1e1 == 0 && s2e2 == 0) {		/* 반례 2 */
        if(s1 > e1) swap(s1, e1);
        if(s2 > e2) swap(s2, e2);
        return s2 <= e1 && s1 <= e2;
    }
    return s1e1 <= 0 && s2e2 <= 0;		/* 반례 1 */
}