.jpg)
Union-Find 알고리즘이란?
서로소 집합(Disjoint-Set) 알고리즘이라고도 불리는 알고리즘으로 구체적으로 여러 개의 노드가 존재할 때 두 개의 노드를 선택해서, 현재 이 노드가 서로 같은 그래프에 속하는지 판별하는 알고리즘입니다.
❓ Disjoint-Set(서로소 집합) 이란 무엇일까요?
👉 서로 중복되지 않는 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료구조입니다. 즉, 공통 원소가 없는 부분 집합들로 나눠진 원소들에 대한 자료구조입니다.
Union-Find 알고리즘의 과정
Union find 알고리즘은 초기화(makeSet) - 합치기(union) - 찾기(find) 연산 과정을 거칩니다.
-
초기화(makeSet)
union과 find 연산을 하기 전, 각 노드를 하나의 집합으로 초기화하는 과정
ex) 0부터 5까지 노드가 있을 때 {0}, {1}, {2}, {3}, {4}, {5} 처럼 하나의 유일한 노드를 가지는 집합으로 만듭니다. -
합치기(union)
두 집합을 합치는 과정
ex) 위의 예시에서 0과 1번 노드를 합친다면 {0,1}, {2}, {3}, {4}, {5} 처럼 집합이 합해져 하나의 집합이 됩니다. -
찾기(find)
주어진 노드가 속한 집합의 대표 노드를 반환
❓ 집합을 어떠한 자료구조로 구현하는 것이 좋을까?
👉 트리 구조가 가장 효율적인 자료구조로서 사용됩니다. 왜냐하면 트리 구조는 루트 노드가 존재하므로 대표 원소로 설정하기 용이합니다.
예시
1부터 6까지 노드가 있을 때 4개의 union 연산 union(1,4), union(2,3), union(2,4), union(5,6) 이 주어진 상태를 예시로 보자.
초기 상태

union 후 상태
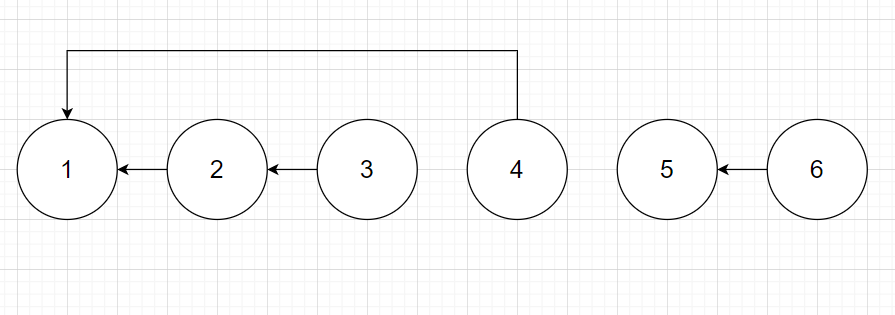
- 부모 테이블 초기화
노드의 개수 크기의 부모 테이블을 초기화 한다. 초기값은 자기 자신을 부모로 가지도록 설정한다.
| 노드번호 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 부모 | 1 | 2 | 3 | 4 | 5 | 6 |
- union 연산
- union(1,4) : 현재 루트 노드는 각각 1과 4이므로 더 큰 번호인 루트 노드 4의 부모를 1로 설정
| 노드번호 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 부모 | 1 | 2 | 3 | 1 | 5 | 6 |
- union(2,3) : 현재 루트 노드는 각각 2와 3이므로 더 큰 번호인 루트 노드 3의 부모를 2로 설정
| 노드번호 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 부모 | 1 | 2 | 2 | 1 | 5 | 6 |
- union(1,2) : 현재 루트 노드는 각각 1와 2이므로 더 큰 번호인 루트 노드 2의 부모를 1로 설정
| 노드번호 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 부모 | 1 | 1 | 2 | 1 | 5 | 6 |
- union(5,6) : 현재 루트 노드는 각각 5와 6이므로 더 큰 번호인 루트 노드 6의 부모를 5로 설정
| 노드번호 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 부모 | 1 | 1 | 2 | 1 | 5 | 5 |
union을 마친 상황
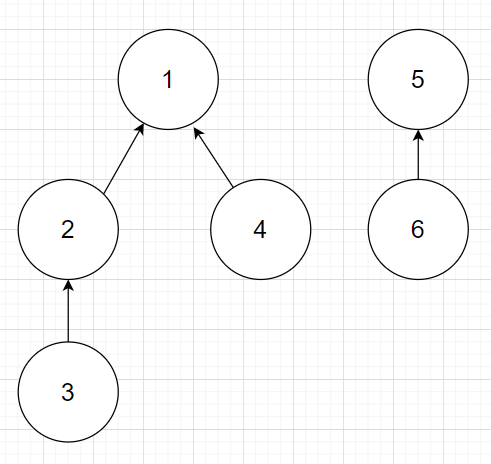
❓ 1과 3은 부모노드가 다른데 같은 집합인지 어떻게 확인할 수 있을까요?
👉 재귀함수를 사용해서 알 수 있습니다. 3의 부모를 찾기 위해서는 먼저 3이 가리키고 있는 2를 찾습니다. 그리고 2의 부모를 확인합니다. 그러면 2의 부모가 1을 가리키고 있으므로 그제서야 결과적으로 3은 1과 같은 집합이라는 것을 알 수 있습니다.
Union-Find 예제
📌 문제
4개의 인수가 매개변수로 들어온다. 첫번째 매개변수로는 노드의 수, 두번째 매개변수로는 연결상태를 나타내는 nums 배열, 3번째 매개변수와 4번째 매개변수로는 두 개의 노드번호가 들어온다. 두 개의 노드가 같은 집합에 속해있으면 YES를 출력하고 다른 집합에 속해있으면 NO를 출력한다.
📌 풀이
function solution(n, nums, s1, s2) {
let answer = "YES";
let parent_node = Array.from({ length: n + 1 }, (v, i) => i);
function Find(v) {
if (v === parent_node[v]) return v;
else return (parent_node[v] = Find(parent_node[v]));
}
function Union(a, b) {
let fa = Find(a);
let fb = Find(b);
if (fa !== fb) parent_node[fa] = fb;
}
for (let [a, b] of nums) {
Union(a, b);
}
if (Find(s1) !== Find(s2)) return "NO";
return answer;
}- 부모 노드를 자기 자신으로 초기화
let parent_node = Array.from({ length: n + 1 }, (v, i) => i);- 두개의 노드번호를 입력받아서 Union하는 함수
function Union(a, b) {
let fa = Find(a);
let fb = Find(b);
if (fa !== fb) parent_node[fa] = fb;
}- 연결 상태인 nums배열을 이용하여 union
for (let [a, b] of nums) {
Union(a, b);
}- 재귀를 이용하여 부모노드를 찾는 Find 함수
function Find(v) {
if (v === parent_node[v]) return v;
else return (parent_node[v] = Find(parent_node[v]));
}- 두 개의 노드가 같은 집합인지 아닌지 확인
if (Find(s1) !== Find(s2)) return "NO";