시간 복잡도와 공간 복잡도는 알고리즘 실행에 필요한 시간의 양과 메모리 공간의 양을 나타내는 척도로써 알고리즘의 성능과 효율성을 평가하는데 중요한 지표이며, 최적의 알고리즘을 선택하기 위해 반드시 고려해야하는 요소이다.
최근 대용량 시스템이 보편화되면서, 공간 복잡도보다는 시간 복잡도가 우선시된다.
시간 복잡도
입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마만큼 걸리는가?
효율적인 알고리즘은 입력값이 커짐에 따라 증가하는 시간의 비율을 최소화한 알고리즘을 뜻한다.
표기하는 방법
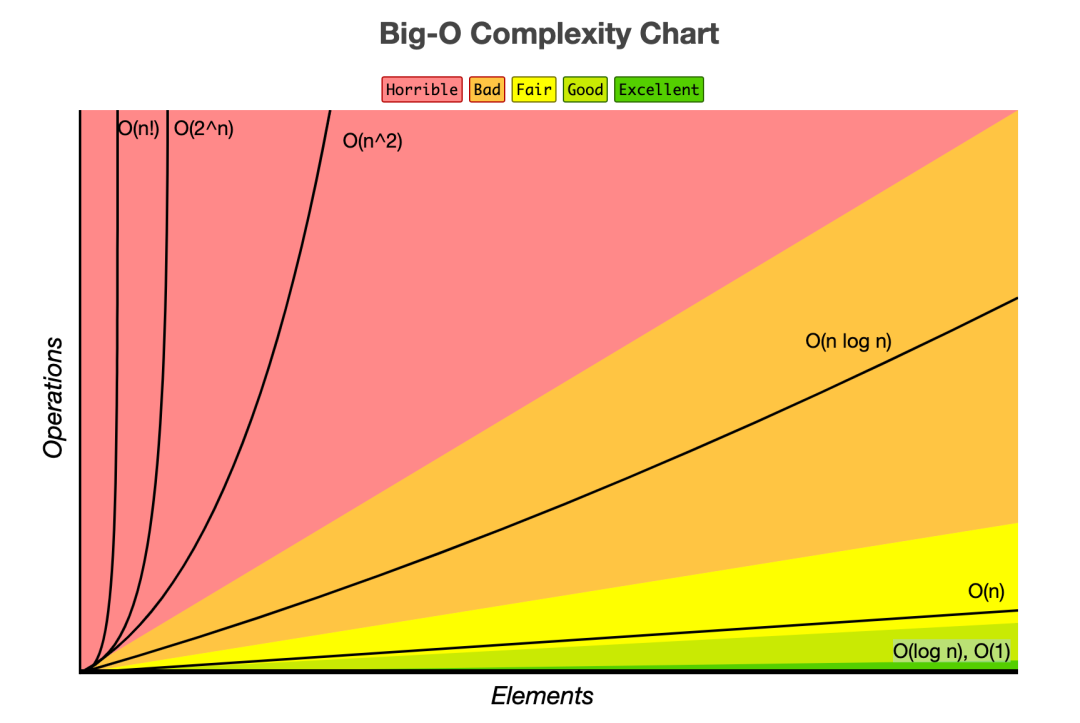
- Big-O(빅-오) ⇒ 상한 점근 (최악)
- Big-Ω(빅-오메가) ⇒ 하한 점근 (최선)
- Big-θ(빅-세타) ⇒ 평균
알고리즘에서는 항상 최악의 경우까지 고려하는 것이 바람직하므로 Big-O표기법을 주로 사용한다.
'최소 이 정도 시간 이상 걸린다' 또는 '이 정도 시간이 걸린다'를 고려하는 것보다 '이 정도 시간까지 걸릴 수 있다'를 고려해야 한다.
Big-O 표기법
- O(1)
- O(n)
- O(log n)
- O(n^2)
- O(2^n)
O(1)
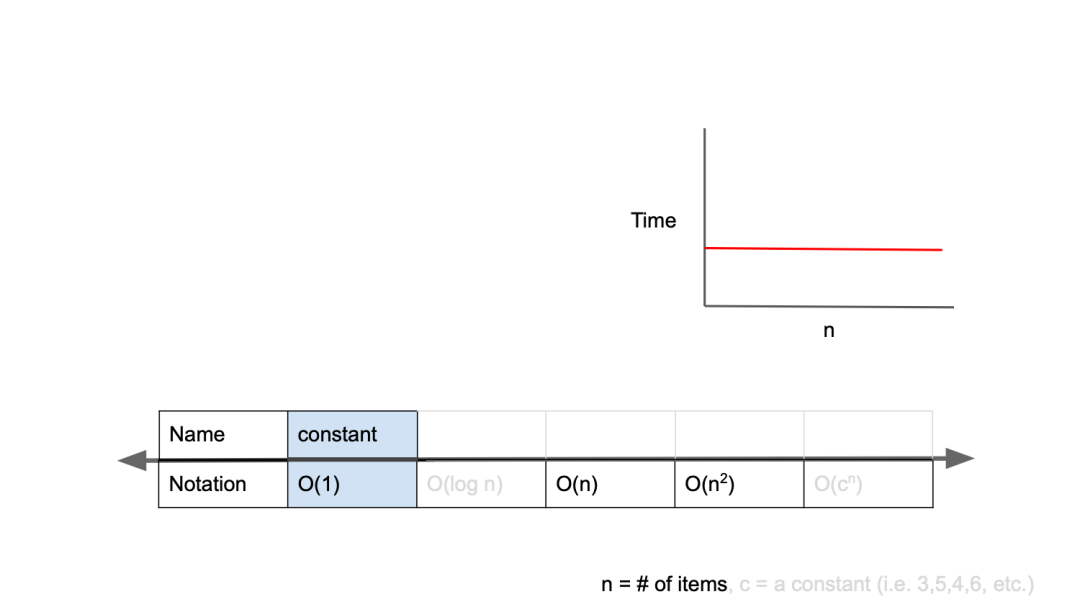
일정한 복잡도라고 하며, 입력값이 증가하더라도 시간이 늘어나지 않는다.
public int algorithm(int[] arr, int index) {
return arr[index];
}
int[] arr = {1, 2, 3, 4, 5};
int index = 1;
int result = algorithm(arr, index);
System.out.println(result);arr의 길이가 아무리 커져도 해당 index에 접근해 값을 즉시 반환할 수 있다.
O(n)
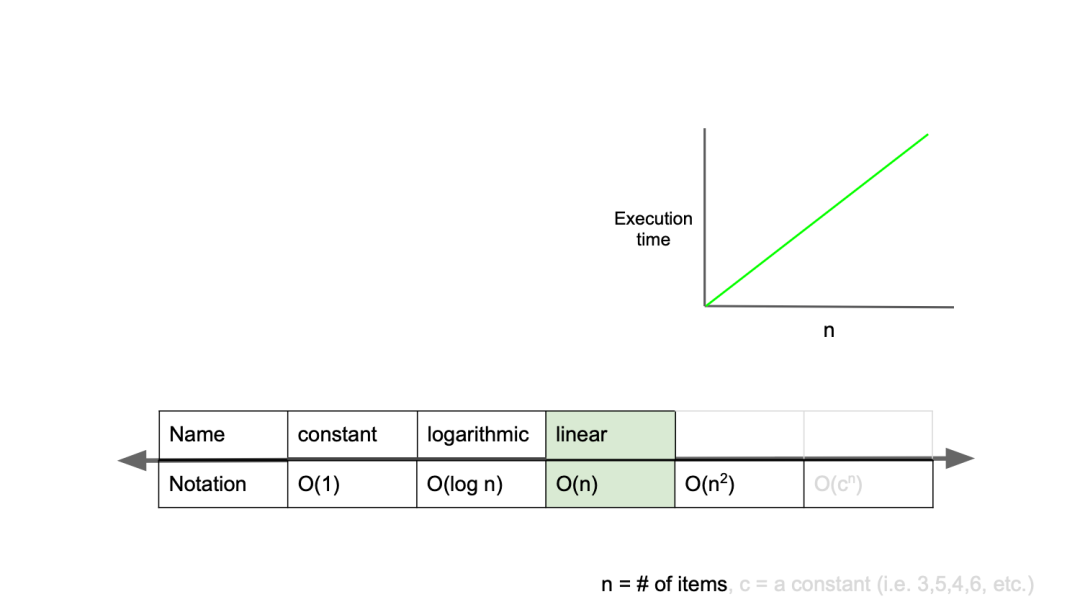
선형 복잡도라고 하며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가한다.
public void algorithm(int n) {
for(int i = 0; i < n; i++) {
// do something for 1 second
}
}
public void algorithm2(int n) {
for(int i = 0; i < n * 2; i++) {
//do something for 1 second
}algorithm 메서드에서는 입력값이 1 증가할 때마다 실행시간이 1초씩 증가한다.
algorithm2 메서드에서는 1 증가할 때마다 2초씩 증가한다.
입력값이 커질수록 n앞의 계수의 의미가 퇴색되기 때문에 계수를 생략해 O(n)으로 표기한다.
O(log n)
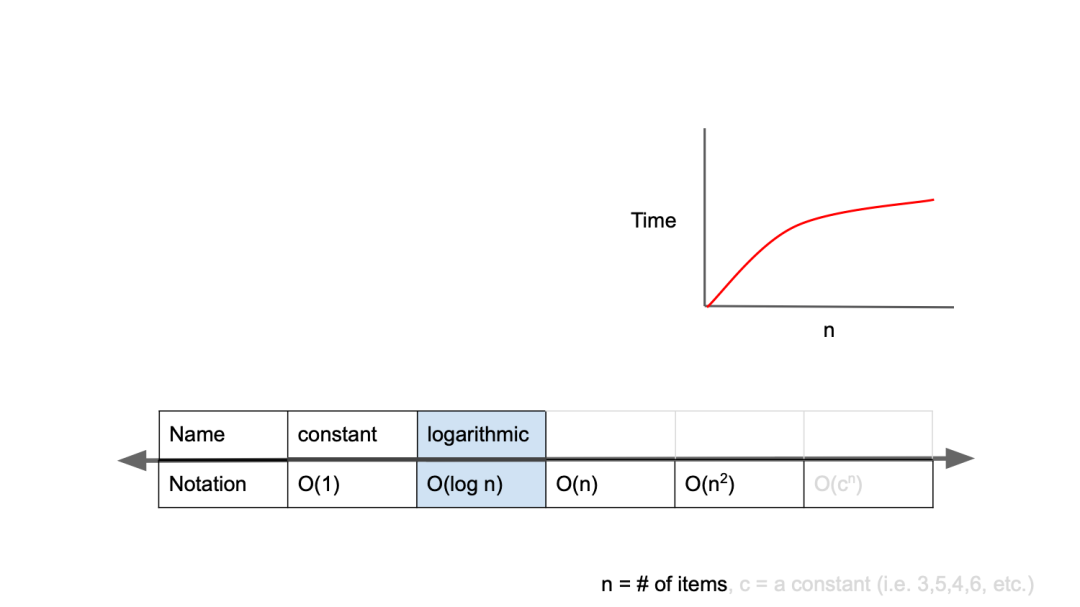
로그 복잡도라고 하며, O(1) 다음으로 빠르다.
public static int binarySearch(int[] arr, int target) {
int start = 0;
int end = arr.length - 1;
while (start <= end) {
int mid = (start + end) / 2;
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
start = mid + 1; // 오른쪽 부분 탐색
} else {
end = mid - 1; // 왼쪽 부분 탐색
}
}
return -1; //탐색 실패
}위 코드는 이분 탐색 알고리즘으로 탐색 범위가 반씩 줄어드는 대표적인 O(log n)의 시간복잡도를 갖는 알고리즘이다.
탐색 범위가 반씩 줄어들기 때문에 범위 n이 주어졌을때, 탐색 횟수를 k라고 한다면,
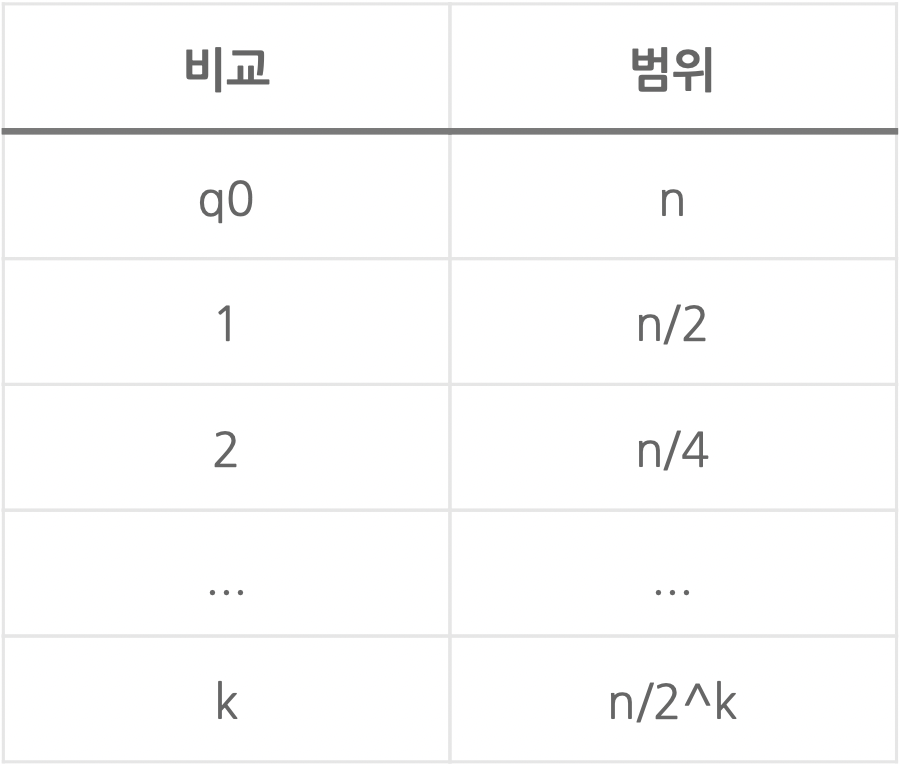
탐색 범위가 더 이상 줄일 수 없는 1이 되었을때 n/2^k = 1 이기 때문에 k = log2n이다.
따라서 이분 탐색의 시간 복잡도는 O(log n)이 된다.
컴퓨터가 이진수 시스템을 사용하기 때문에, 로그는 밑을 대부분 2로 사용한다. 즉, log2n, 때때로는 log n 이라고 쓰임. (위키백과)
O(n^2)
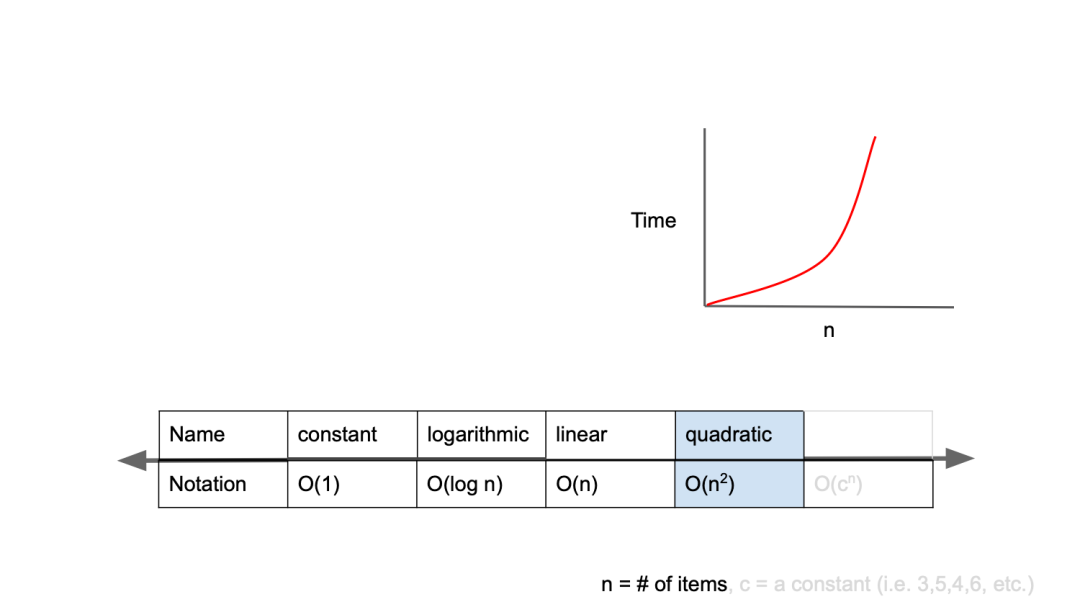
2차 복잡도라고 하며, 입력값이 증가함에 따라 시간의 n의 제곱의 비율로 증가한다.
public void algorithm(int n) {
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
//do something for 1 second
}
}
}
public void algorithm2(int n) {
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
for(int k = 0; k < n; k++) {
//do something for 1 second
}
}
}
}O(n)과 같이 n이 커질수록 지수의 영향력이 퇴색되기 때문에 O(n^2)로 표기한다.
O(2^n)
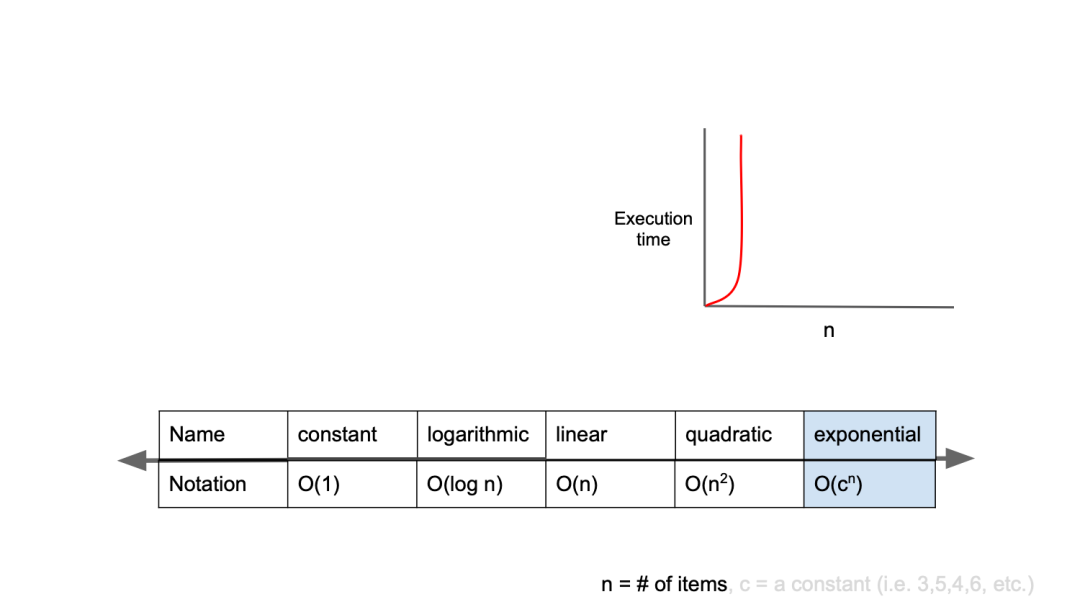
기하급수적 복잡도라고 하며, 가장 느린 시간 복잡도를 가진다.
public int fibonacci(int n) {
if(n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}재귀함수로 구현된 피보나치 수열로 O(2^n)의 대표적인 알고리즘이다.
공간 복잡도
프로그램을 실행 및 완료하는데 필요한 저장공간의 양
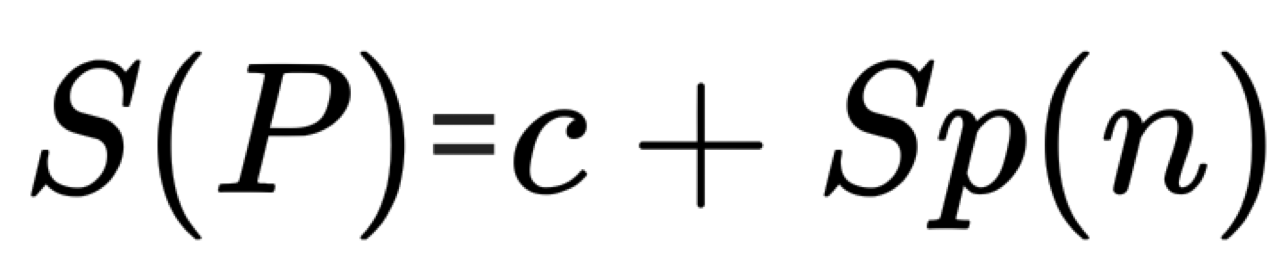
총 필요 저장공간(S(P)) = 고정 공간(c) + 가변 공간(Sp(n))
고정 공간(c)는 상수이기 때문에 공간 복잡도는 가변 공간에 의해서 좌우된다.
- 고정 공간 - 코드 저장 공간(단순 변수 및 상수)
- 가변 공간 - 실행 중 동적으로 필요한 공간
O(1)
public int factorial(int n) {
int fac = 1;
for(int i = 1; i <= n; i++) {
fac = fac * i;
}
return fac;
}n의 값에 상관없이 변수 n, fac, i만 필요하기 때문에 고정적인 메모리를 사용한다.
따라서 공간복잡도 O(1)를 갖는다.
O(n)
public int factorial(int n) {
if (n > 1) {
return n * factorial(n - 1);
} else {
return 1;
}
}재귀함수로 구현된 펙토리얼로 변수 n이 n개 만들어진다.
따라서 메모리에 n부터 1까지 쌓여 공간 복잡도 O(n)을 가진다.
