복잡도

1. 시간 복잡도

1-1. 정의

Time Complexity

알고리즘이 입력 크기에 따라 얼마나 많은 연산을 수행하는지 나타내는 척도다.
알고리즘의 성능과 효율을 평가하는 데 사용된다.

1-2. 빅오(Big O)표기법

알고리즘의 시간 복잡도는 보통 빅오 표기법으로 나타낸다.

빅오 표기법이란, 입력된 N의 크기가 매우 큰 경우 해당하는 알고리즘의 실행 시간의 상한을 나타낸다.

다음과 같은 코드를 예시로 보면 N이 주어졌을 때 알고리즘 실행시간은 10N2 + N이며, 빅오표기법으로 나타내면 O(n2 )이다.

시간의 증가 속도를 고려했을 때 가장 영향을 많이 끼치는 항만 고려해 표기한 것이다. n2에 비해 n이 증가하는 속도는 비교가 되지 않기 때문이다.

for i in range(10):
    for j in range(N):
        for k in range(N):
            print(i, j, k)
            
for m in range(N):
    print(m)

1-3. 시간 복잡도 속도

다음은 시간 복잡도의 속도를 비교한 그래프다.

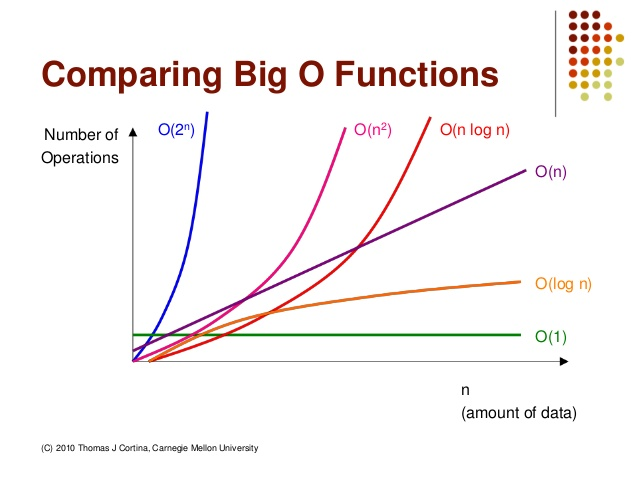
그래프만 보더라도 시간 복잡도에 따른 속도의 차이를 실감할 수 있다. 이처럼 알고리즘의 성능과 효율을 위해서는 시간복잡도를 충분히 고려하는 것이 필요하다.

2. 공간 복잡도

Space Complexity

2-1. 정의

알고리즘이 실행될 때 메모리 공간이 얼마나 필요한지 나타내는 것이다.

즉, 입력된 데이터를 기반으로 알고리즘을 실행할 때 필요한 메모리 양을 분석하는 것이다. 공간복잡도도 보통 빅오 표기법을 사용해 표현된다.

2-2. 공간 복잡도 분석

공간 복잡도를 아주 정확하게 분석을 위해서는 다음과 같이 세 가지를 고려해야 한다.

1. 입력 데이터

• 입력 데이터를 저장하기 위한 메모리 공간

2. 추가적인 데이터 구조

• 알고리즘을 수행하는 동안 생성되는 추가적인 데이터 구조

3. 재귀 호출

• 재귀 함수를 호출하는 경우 재귀 호출 스택에 필요한 메모리 공간

2-3. 공간 복잡도 빅오 표기법

공간복잡도도 시간복잡도와 마찬가지로 빅오 표기법을 사용한다. 깊이 들어가면 끝도 없으니 아주 간단한 예시만 살펴보자.

def sum_of_array(arr):
    total_sum = 0
    for num in arr:
        total_sum += num
    return total_sum

위 알고리즘의 공간 복잡도는 O(1)이다. 배열의 원소를 하나씩 훑어가며 알고리즘 내에서는 total_sum이라는 변수 하나에 값을 누적하기 때문에 공간 복잡도는 입력된 배열의 크기와 관계 없이 일정하다.

만약 크기가 N인 배열을 입력받아 알고리즘 내부에서 N*N인 배열을 생성한다면, 이 알고리즘의 공간 복잡도는 O(n2 )이 될 것이다.

3. 마무리

시간 복잡도와 공간 복잡도는 반비례적인 경향이 있으며, 현재 대용량 시스템이 보편화되면서 시간복잡도를 더 우선시하고 있다.