[프로그래머스] 땅따먹기

🔗 문제 링크

https://programmers.co.kr/learn/courses/30/lessons/12913

🤔 문제

땅따먹기 게임을 하려고 합니다. 땅따먹기 게임의 땅(land)은 총 N행 4열로 이루어져 있고, 모든 칸에는 점수가 쓰여 있습니다. 1행부터 땅을 밟으며 한 행씩 내려올 때, 각 행의 4칸 중 한 칸만 밟으면서 내려와야 합니다. 단, 땅따먹기 게임에는 한 행씩 내려올 때, 같은 열을 연속해서 밟을 수 없는 특수 규칙이 있습니다.

예를 들면,

| 1 | 2 | 3 | 5 |

| 5 | 6 | 7 | 8 |

| 4 | 3 | 2 | 1 |

로 땅이 주어졌다면, 1행에서 네번째 칸 (5)를 밟았으면, 2행의 네번째 칸 (8)은 밟을 수 없습니다.

마지막 행까지 모두 내려왔을 때, 얻을 수 있는 점수의 최대값을 return하는 solution 함수를 완성해 주세요. 위 예의 경우, 1행의 네번째 칸 (5), 2행의 세번째 칸 (7), 3행의 첫번째 칸 (4) 땅을 밟아 16점이 최고점이 되므로 16을 return 하면 됩니다.

📌 제한사항

• 행의 개수 N : 100,000 이하의 자연수
• 열의 개수는 4개이고, 땅(land)은 2차원 배열로 주어집니다.
• 점수 : 100 이하의 자연수

😮 문제 해결 방법

한 행씩 내려올 때마다 같은 열을 연속해서 밟을 수 없기 때문에 내려온 열의 최댓값은 내려오기 전 행의 다른 인덱스의 값과 내려온 열의 인덱스를 더해 최댓값이 된다.

내려간 행의 값을 메모해놓기 위해 DP 2차원 배열을 선언한다.

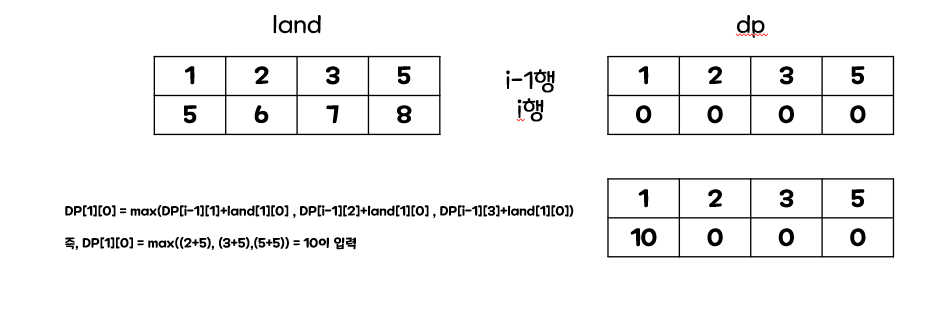
입력 예제를 보면, 1,2,3,5행을 i-1행이라하고 5,6,7,8 내려갈 행(현재 행)을 i행이라하자.

그렇다면 i행의 첫번째 인덱스가 될 수 있는 최댓값은 i-1행의 첫번째 인덱스를 제외한 값과 i행의 첫번째 인덱스의 값을 더한 값중 최댓값이다. 따라서 구한 최댓값을 dp배열의 i행 첫번째 인덱스에 넣어주면 된다. 이러한 작업을 나머지 인덱스에 반복하고, land의 사이즈만큼 반복해준 후 마지막열의 최댓값을 뽑아오면 문제가 해결된다.

🚩 Java 코드

package com.algorithm.Programmers.Lv2;

public class Solution_12913 {

    public static void main(String[] args) {
        int[][] land = {{1,2,3,5},{5,6,7,8},{4,3,2,1}};
        System.out.println(solution(land));
    }
    static int solution(int[][] land) {

        int[][] dp = new int[land.length][4];
        int idx = dp.length-1;
        
        //첫 dp부분에 첫번째 행 값 넣어주기
        for(int i=0;i<4;i++)
            dp[0][i] = land[0][i];

        for(int i=1;i<land.length;i++){
            for(int j=0;j<4;j++){
                int max = 0;
                //점화식 max(memo한 부분과 현재 값을 더해 최대값)
                for(int k=0;k<4;k++){
                    if(j!=k)
                        max = Math.max(max, land[i][j] + dp[i-1][k]);
                }
                dp[i][j] = max;
            }
        }
        
        //마지막열 최댓값 뽑아오기
        return Math.max(Math.max(dp[idx][0],dp[idx][1]),Math.max(dp[idx][2],dp[idx][3]));
    }
}

💬 코멘트

처음에 메모할 DP배열을 1차원 배열로 선언하고 문제를 접근해서 풀이에 애를 먹었다. 결국 2차원 배열로 선언하고 풀이하였다. 동적 프로그래밍(Dynamic Programming)이 아직 많이 서툴어서 시간을 많이 잡아먹고 생각도 많이 한 것 같다.