[Algorithm] 백준 1004

ZEDY·2024년 3월 13일

백준 코딩테스트 파이썬

[코딩테스트] 알고리즘 문제풀이

목록 보기

10/46

나는 왜 이렇게 어렵게 문제를 접근하는 걸까......... 🥹
울고 싶다................

문제

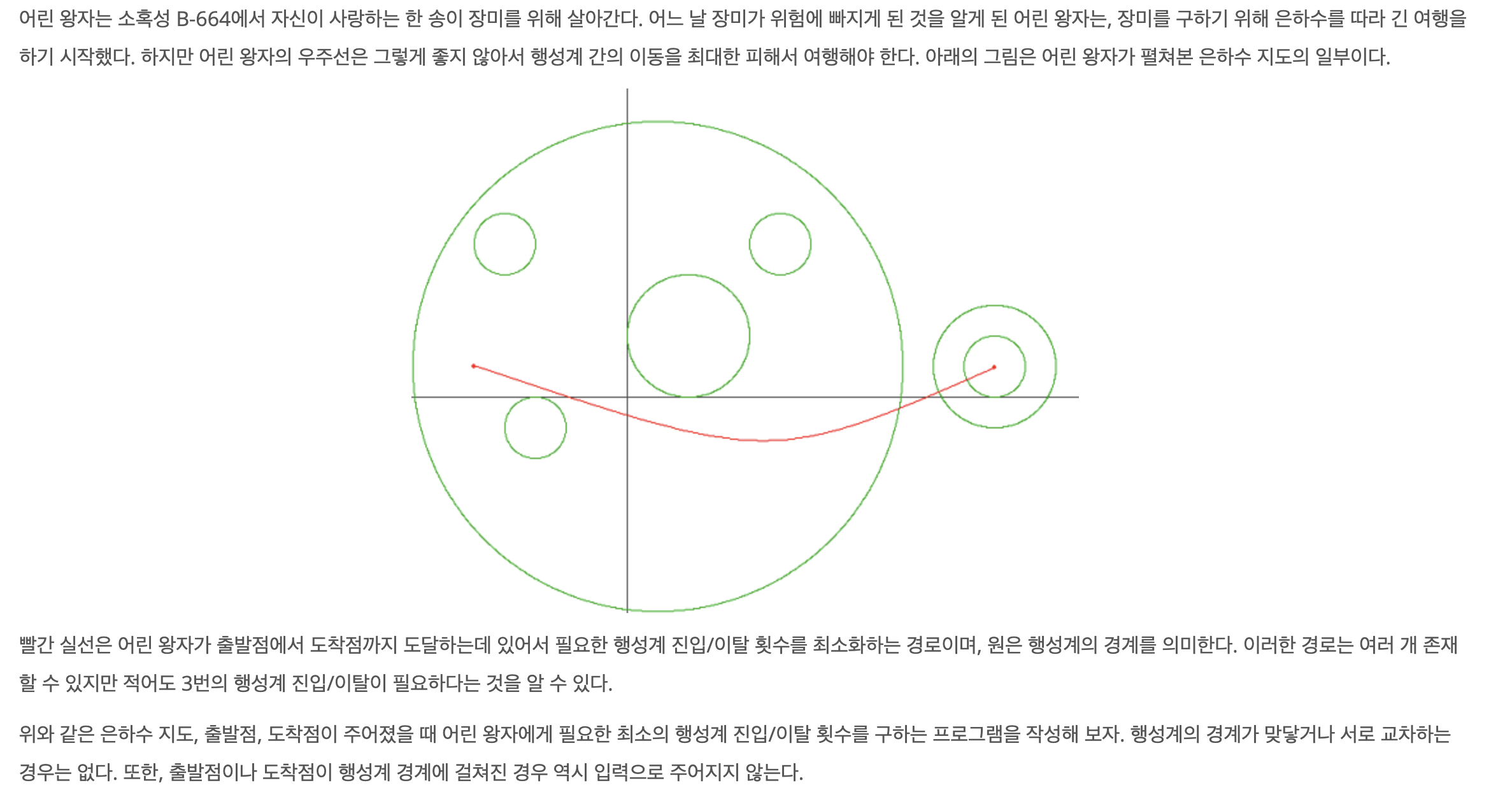
처음엔 이게 뭔 소린가 했다.

풀이

첫번째 접근법 : 삽질 1

출발점에서부터 8방으로 이동하며, 경계가 가장 적은 점을 선택해 방문하는 방법
1. 방문한 경로 기록할 테이블 필요
2. 방문하지 않았다면 방문 후 , 방문 테이블에 표시

자.. 이 알고리즘의 문제점은 도착 정점에 도달하지 않을 가능성도 있다는 것이다. 물론 -1000 <-> -1000이라는 제한이 있지만, 절대 효율적이지 않다.
모든 경우의 수를 다 방문하고 그 중에서 최소값만 취하는 것이기 때문에 경로가 진짜 이상하게 나올 것이다.
구현하다가 탈락..

두번째 접근법 : 삽질 2

행성 경계선을 미리 그래프에 그리고 회피하면서 선택해서 가려고 했음
어떻게 그리지..? 에-바

그리고 회피하며 선택하는데 갇힐 확률이 존재한다.

세번째 접근법 : 정답

1. 경계선을 넘나드는 횟수 count의 기준

출발점이 행성 A 안에 있고 and 도착점이 행성 A 안에 있는 경우 -> 0
출발점이 행성 A 안에 있고 and 도착점이 행성 A 밖에 있는 경우 -> 1
출발점이 행성 A 밖에 있고 and 도착점이 행성 A 안에 있는 경우 -> 1
출발점이 행성 A 밖에 있고 and 도착점이 행성 A 밖에 있는 경우 -> 0

우주선은 알아서 행성을 잘 피해 가겠지,, 라는 생각으로 이 문제를 접근했어야 한다.

모든 행성에 대해 loop를 돌면서 카운팅을 한다.

정답 코드

import math

n = int(input())

for i in range(0, n):
    start_x, start_y, end_x, end_y = map(int, input().split(' '))
    num = int(input())
    cnt = 0
    planet = []
    for j in range(0, num):
        x = list(map(int, input().split(' ')))
        planet.append(x)
    for j in range(0, num):
        if (math.sqrt((start_x - planet[j][0])**2 + (start_y - planet[j][1])**2) < planet[j][2] and math.sqrt((end_x - planet[j][0])**2 + (end_y - planet[j][1])**2) > planet[j][2]) or(
        math.sqrt((start_x - planet[j][0])**2 + (start_y - planet[j][1])**2) > planet[j][2] and math.sqrt((end_x - planet[j][0])**2 + (end_y - planet[j][1])**2) < planet[j][2]):
            cnt += 1
    print(cnt)