[백준] 11057

문제 개요

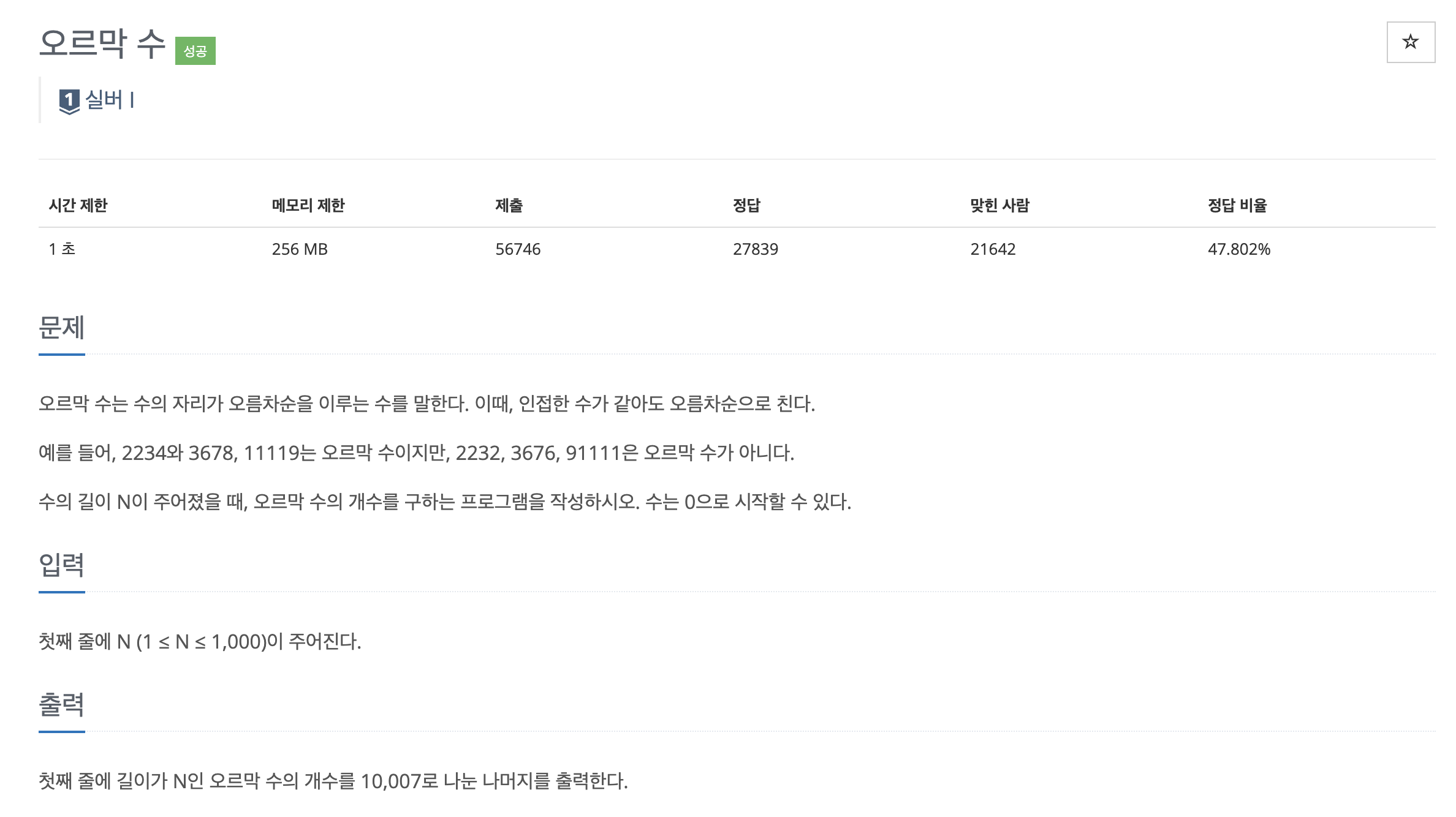
주어진 문제는 수의 자리가 오름차순을 이루는 경우의 수를 구하는 것입니다. 수는 0으로 시작할 수 있으며, 길이가 N인 오르막 수의 개수를 계산해야 합니다.

접근 방법

이 문제는 동적 계획법(Dynamic Programming)을 활용하여 해결할 수 있습니다. 각 자리에서 가능한 오르막 수의 개수를 계산하는 방법을 설명하겠습니다.

1. 기본 아이디어:
   각 자리에서 오르막 수를 이루기 위해 가능한 수의 개수를 저장합니다. 앞자리의 수가 뒤 자리보다 작거나 같은 경우 오르막 수가 됩니다.

2. 점화식 유도:

   • dp[i][j]는 길이가 i이고 마지막 자리가 j인 오르막 수의 개수를 의미합니다.
   • dp[i][j] = dp[i][j-1] + dp[i-1][j]
   • 이는 마지막 자리가 j인 오르막 수는 마지막 자리가 j-1인 오르막 수에 현재 자리 j를 추가하거나, i-1 길이에서 j인 경우를 추가하는 두 가지 경우의 수를 의미합니다.

3. 초기 조건 설정:

   • dp[0][j] = 1: 길이가 0인 경우는 모든 자리에서 1가지 경우만 있습니다.

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class P11057 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        int[][] dp = new int[n+1][10];
        
        for(int i = 0; i < 10; i++){
            dp[0][i] = 1;
        }

        for(int i = 1; i < n + 1; i++){
            dp[i][0] = 1;
            for(int j = 1; j < 10; j++){
                dp[i][j] = (dp[i][j-1] + dp[i-1][j]) % 10007;
            }
        }
        
        System.out.println(dp[n][9]);
    }
}

사고 과정 설명

1. 문제 이해:
   오르막 수는 각 자리의 숫자가 같거나 커지는 수를 의미합니다. 문제에서 요구하는 것은 길이가 N인 오르막 수의 총 개수를 구하는 것입니다.

2. 동적 계획법 배열 정의:

   • dp[i][j]는 길이가 i이고 마지막 자리가 j인 오르막 수의 개수를 저장합니다.

3. 점화식 유도:

   • dp[i][j] = dp[i][j-1] + dp[i-1][j]로 점화식을 설정합니다. 이 점화식은 현재 자리의 수가 j일 때, 이전 자리의 수가 j 이하인 모든 경우를 더해줍니다.

4. 초기 조건 설정:

   • dp[0][j] = 1로 설정하여, 길이가 0인 경우를 모두 1로 초기화합니다.

5. 결과 출력:

   • 최종적으로 dp[n][9]를 출력하여 길이가 N인 모든 오르막 수의 개수를 계산합니다.

결론

이 접근 방법은 동적 계획법을 활용하여 효율적으로 오르막 수의 개수를 계산합니다. 점화식을 통해 문제를 단계적으로 해결하며, 큰 문제를 작은 부분 문제로 나누어 해결하는 방법을 배울 수 있는 좋은 예제입니다.

알고리즘 구현보다 사고과정이 어려웠던 문제이다.