문제
K개의 소수가 있다. 이때, 이 소수들 중에서 몇 개를 곱해서 얻게 되는 수들이 있을 것이다. 소수들을 선택할 때에는 같은 수를 선택해도 되며, 주어지는 소수 자체도 포함시키자.
예를 들어 세 소수가 2, 5, 7이었다면, 이러한 곱들을 오름차순으로 나타내 보면, 2, 4, 5, 7, 8, 10, 14, 16, 20, 25, 28, 32, 35, 등이 된다.
K개의 소수가 주어졌을 때, 이러한 소수의 곱들 중에서 N번째 수를 구해 보자. 단 정답은 231보다 작은 자연수이다.
입력
첫째 줄에 K(1 ≤ K ≤ 100), N(1 ≤ N ≤ 100,000)이 주어진다. 다음 줄에는 K개의 소수가 오름차순으로 주어진다. 같은 소수가 여러 번 주어지는 경우는 없으며, 주어지는 소수는 모두 541보다 작거나 같은 자연수이다.
출력
첫째 줄에 문제에서 설명한 대로 소수의 곱을 나열했을 때, N번째 오는 것을 출력한다.
접근
예를 들어, 4개의 소수 2,3,5,7이 있다고 가정해보자.
1. 2,3,5,7의 소수를 우선순위 큐 (오름차순 정렬)에 넣어준다.
2. 우선순위 큐에서 2를 빼내고, 2,3,5,7 각각을 곱해준 값을 우선순위 큐에 넣어준다. (2x2, 2x3, 2x5, 2x7)
3. 2번 과정을 N번 반복 후, 우선순위 큐에서 N번째 뺀 값이 정답으로 출력.
하지만, 이 과정은 중복된 수를 넣을 수 있기 때문에 예외처리를 해줘야 한다.
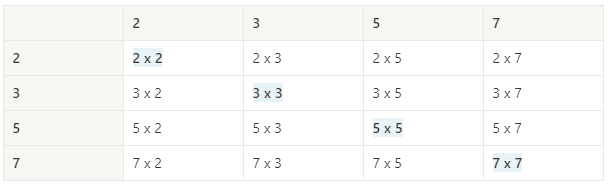
위는 2,3,5,7을 서로 각각 한번씩만 곱한 경우이다.
파란색으로 표시된 부분을 기점으로, 양방향의 수들이 중복된다는 것을 알 수 있다.
따라서, 각 과정에서 중복되는 수를 저장하지 않기 위해 우선순위 큐에서 꺼낸 값을 입력받은 K개의 소수들과 나누어 보면서, 나누어 떨어지지 않는 수 까지 저장하다가, 나누어 떨어지는 수가 발견되면 그 수 까지 우선순위 큐에 저장한 후 반복문을 종료하면 된다.
import java.io.*;
import java.util.*;
public class Main {
static int K, N;
static long ans;
static long[] arr;
static PriorityQueue<Long> pq;
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
K = Integer.parseInt(st.nextToken());
arr = new long[K];
N = Integer.parseInt(st.nextToken());
pq = new PriorityQueue<>();
st = new StringTokenizer(br.readLine());
for(int i=0;i<K;i++) {
arr[i] = Integer.parseInt(st.nextToken());
pq.add(arr[i]);
}
ans = 0;
while(N-- > 0) {
ans = pq.poll();
for(int i=0;i<K;i++) {
// 정답이 2^31보다 작아야함
if ((ans * arr[i]) >= ((long) 2 << 30)) break;
pq.offer(ans * arr[i]);
// 현재 소수로 나누어 떨어지는 수가 발견되면 종료
// 중복된 값을 배제하기 위함
if (ans % arr[i] == 0) break;
}
}
System.out.println(ans);
}
}- 참고 블로그 : https://steady-coding.tistory.com/89
