📋 그래프 정점 표현 학습
📌 정점 표현 학습
- 정점 표현 학습 간단히 정점 임베딩(Node Embedding)은 그래프의 정점들을 벡터 형태로 표현하는 것
- 정점 임베딩 결과로, 벡터 형태의 데이터를 위한 도구들을 그래프에도 적용할 수 있다. ex) 로지스틱 회귀분석, 다층 퍼셉트론, K-Means
- 정점 표현 학습의 목표는
그래프에서 정점간 유사도를 임베딩 공간에서도 '보존' 하는것
- 임베딩 공간에서의 유사도는 내적(Inner Product)를 사용한다
1) 그래프에서의 정점 유사도를 정의
2) 정의한 유사도를 보존하도록 정점 임베딩을 학습한다.
📌 인접성 기반 접근법
- 인접성 기반 접근법에서는 두 정점이 인접할 때 유사하다고 간주
- 다음 손실함수가 최소가 되는 정점 임베딩을 찾는 것을 목표로 한다
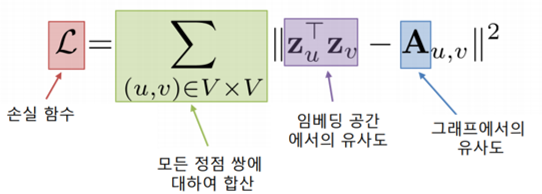
- 그러나 인접성만으로 유사도를 판단하는 것은 한계가 있다.
📌 거리/경로/중첩 기반 접근법
- 거리 기반 접근법에서는 두 정점 사이의 거리가 충분히 가까운 경우 유사하다고 간주
- 경로 기반 접근법에서는 두 정점 사이의 경로가 많을 수록 유사하다고 간주
- 중접 기반 접근법에서는 두 정점이 많은 이웃을 공유할 수록 유사하다고 간주
📌 임의보행 기반 접근법
- 임의보행 기반 접근법에서는 한 정점에서 시작하여 임의보행 할 때 다른 정점에 도달할 확률을 유사도로 간주한다.
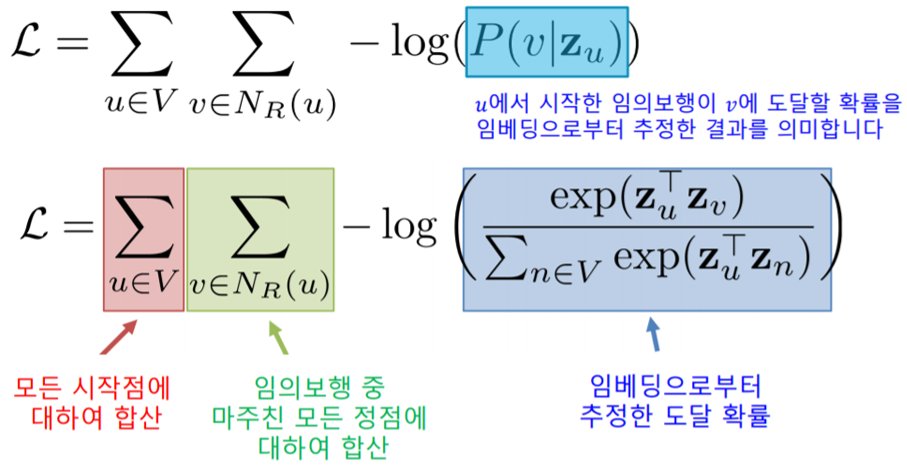
- Node2Vec은 2차 치우친 임의보행을 사용한다.
현재 정점과 직전에 머물렀던 정점을 모두 고려하여 다음 정점을 선택
📌 변환식 정점 표현 학습의 한계
- 변환식(Transductive) 방법은 학습의 결과로 정점의 임베딩 자체를 얻는다는 특성
정점을 임베딩으로 변화시키는 함수 즉 인코더를 얻는 귀납식(Inductive) 방법과 대조

