알고리즘을 풀이할 때 그래프를 탐색할 때 사용하는 방법이다.
공통적으로 이 두 방법은 모두 모든 노드를 방문하는 목적으로 사용된다.
간단하게 용어를 정의하고 가려고 한다.
그래프의 기본적인 용어
- 노드(정점): 데이터를 담는 지점
- 간선: 노드들을 연결하는 선. 노드간의 관계
- 인접 노드: 하나의 노드에 연결된 다른 노드(간선으로 연결되어진 노드)
- 차수: 하나의 노드에 연결된 간선의 수. 방향그래프의 경우 나가는 차수와 들어오는 차수로 나눈다.
- 경로: 그래프에서 A 노드에서 B 노드로 이동하는데 사용된 간선들의 순서
- 사이클: 시작 노드와 끝 노드가 동일한 경로
- 연결성: 그래프 내에서 노드들 간의 연결 상태
그래프에 대해서 이해하기 위해서 참조한 개발자 소들이 블로그 이다.(자주 도움이 되는 곳이라 꾸준히 방문하게 되는 것 같다.)
깊이 우선 탐색 (DFS, Depth First Search)
- 시작 노드로부터 한 방향으로 깊이 탐색하고, 더 이상 탐색할 것이 없을 때 시작노드에서 다른 방향으로 탐색한다.
- 스택 또는 재귀함수를 사용한다.
- 장점
- 메모리 사용이 좋다. (스택으로 LIFO, Last In First Out)
- 깊은 경로를 빠르게 찾을 수 있다.
- 단점
- 최단 경로를 보장하지 않는다.
- 무한 루프에 빠질 수 있다. (순환 구조에서 만약에 이미 방문한 노드를 다시 방문하지 않게 설정하지 않는다면 무한 루프에 빠질 수 있다. 이러한 내용은 BFS에서도 동일하게 작용할 수 도있다.)
- 깊은 경로를 우선적으로 탐색하기 때문에, 목표 지점이 깊은 곳에 있을 경우 비효율적이다. (탐색의 순서가 없고 목표 지점을 찾기 전에 현재의 경로의 최대한의 깊이를 탐색하므로 최단 경로를 찾는것이 보장되지 않는다.)
너비 우선 탐색 (BFS, Breadth First Search)
- 시작 노드로부터 인접한 노드를 먼저 탐색하는 방법
- 큐를 사용한다.
- 탐색할 수 없을 때까지 같은 레벨의 모든 노드를 방문한 후, 다음 레벨의 노드를 탐색한다.
- 장점
- 최단 경로를 보장. (목표 지점에 가장 먼저 도달하는 경로를 찾음)
- 단점
- 메모리 사용이 많다. (큐로 FIFO, First In First Out. 데이터가 나갈 때마다 한칸씩 데이터가 이동해야하므로 이러한 이동 작업으로 메모리 사용량이 늘어난다.)
- 깊은 경로를 먼저 탐색하지 못할 수 있다. (레벨 순서대로 내려가기 때문에)
DFS와 BFS의 예시
'개발자 소들이님의 블로그'의 예시를 통해서 사용하였습니다.
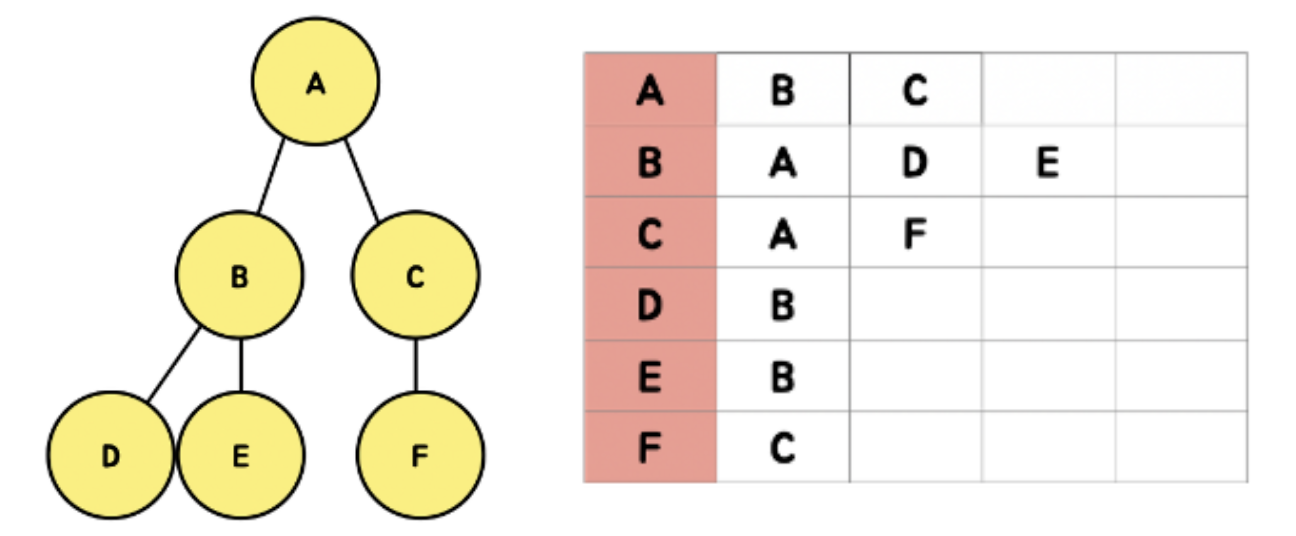
DFS
- 방문을 해야하는 노드를 Stack에 저장
- 이미 방문한 노드를 Queue에 저장
예시 코드
func DFS(graph: [String: [String]], start: String) -> [String] {
var visitedQueue: [String] = []
var needVisitStack: [String] = [start]
while !needVisitStack.isEmpty {
let node: String = needVisitStack.removeLast()
if visitedQueue.contains(node) { continue }
visitedQueue.append(node)
needVisitStack += graph[node] ?? []
}
return visitedQueue
}1. A부터 탐색을 진행
처음에는 방문해야할 노드에만 A가 존재한다.
방문한 노드: []
방문해야할 노드: ["A"]2. A는 탐색 완료
A는 이미 방문을 하였고, 인접 리스트를 통해서 앞으로 방문해야할 노드는 B와 C가 있다.
방문한 노드: ["A"]
방문해야할 노드: ["B", "C"]3. 방문해야할 노드는 스택으로 이루어져있으므로 마지막 노드부터 탐색
DFS의 경우 Stack으로 구성되어있기 때문에, LIFO 마지막으로 들어온 값을 먼저 추출하게된다. 그리하여 C의 노드를 방문하고, 앞으로 방문해야할 노드는 B와 C의 인접 노드인 A와 F가 들어오게 된다.
이 때, 순서는 상관이 없기 때문에 C가 아닌 B가 먼저 탐색할 수도 있다. 대신 그때 2단계에서 방문해야할 노드가 ["C", "B"] 의 형태로 저장되어 있어야한다.
방문한 노드: ["A", "C"]
방문해야할 노드: ["B", "A", "F"]4. 방문해야할 노드에서 마지막 노드를 탐색
위와 동일하게 방문해야할 노드에서 마지막 F를 탐색하고, 인접 노드인 C를 방문해야할 노드에 추가한다.
방문한 노드: ["A", "C", "F"]
방문해야할 노드: ["B", "A", "C"]5. 이미 방문을 했었던 노드의 경우 방문한 노드에 추가되지 않는다.
4단계에서 방문해야할 노드를 확인하였을 때, 앞으로 방문해야할 노드는 C가 된다. 하지만 이는 이미 방문한 노드가 된다. 그리하여 이때의 노드는 방문한 노드에 추가되지 않는다.
한번 더 진행하더라도 A의 노드는 이미 방문이 완료되었기 때문에 추가되지 않고 다음 단계로 넘어가게된다.
방문한 노드: ["A", "C", "F"]
방문해야할 노드: ["B", "A"]
방문한 노드: ["A", "C", "F"]
방문해야할 노드: ["B"]6. 방문해야할 노드가 없어질 때까지 작업을 진행
5단계에서 방문해야할 노드 B를 방문하면서 인접 노드 A, D, E가 방문해야할 노드에 추가가 된다. 그리고 다음 작업을 진행하게되면 마지막 노드인 E를 방문과 동시에 방문해야할 노드에 B가 추가되고, 이는 이미 방문하였기에 제외된다.
마지막으로 D를 방문한 후 방문해야할 노드에 남은 노드들은 이미 방문을 했었던 곳이다. 그리하여 단계가 진행되더라도 방문한 노드에는 추가되지 않고, 방문해야할 노드에서 사라진다.
결과적으로 방문해야할 노드가 비어있게 된다면 모든 과정이 끝이난다.
방문한 노드: ["A", "C", "F", "B"]
방문해야할 노드: ["A", "D", "E"]
방문한 노드: ["A", "C", "F", "B", "E"]
방문해야할 노드: ["A", "D", "B"]
방문한 노드: ["A", "C", "F", "B", "E"]
방문해야할 노드: ["A", "D"]
방문한 노드: ["A", "C", "F", "B", "E", "D"]
방문해야할 노드: ["A", "B"]
방문한 노드: ["A", "C", "F", "B", "E", "D"]
방문해야할 노드: ["A"]
방문한 노드: ["A", "C", "F", "B", "E", "D"]
방문해야할 노드: []BFS
- 방문을 해야하는 노드를 Queue에 저장
- 이미 방문한 노드를 Queue에 저장
예시 코드
func BFS(graph: [String: [String]], start: String) -> [String] {
var visitedQueue: [String] = []
var needVisitQueue: [String] = [start]
while !needVisitQueue.isEmpty {
let node: String = needVisitQueue.removeFirst()
if visitedQueue.contains(node) { continue }
visitedQueue.append(node)
needVisitQueue += graph[node] ?? []
}
return visitedQueue
}1. A부터 탐색을 진행
처음에는 방문해야할 노드에만 A가 존재한다.
방문한 노드: []
방문해야할 노드: ["A"]2. A는 탐색 완료
A는 이미 방문을 하였고, 인접 리스트를 통해서 앞으로 방문해야할 노드는 B와 C가 있다.
방문한 노드: ["A"]
방문해야할 노드: ["B", "C"]3. 방문해야할 노드는 큐로 이루어져있으므로 첫번째 노드부터 탐색
DFS의 경우 Queue으로 구성되어있기 때문에, FIFO 첫번째로 들어온 값을 먼저 추출하게된다. 그리하여 B의 노드를 방문하고, 앞으로 방문해야할 노드는 C와 B의 인접 노드인 A와 D, E가 들어오게 된다.
방문한 노드: ["A", "B"]
방문해야할 노드: ["C", "A", "D", "E"]4. 방문해야할 노드에서 첫번째 노드를 탐색
위와 동일하게 방문해야할 노드에서 첫번째 C를 탐색하고, 인접 노드인 A와 F를 방문해야할 노드에 추가한다.
방문한 노드: ["A", "B", "C"]
방문해야할 노드: ["A", "D", "E", "A", "F"]5. 이미 방문을 했었던 노드의 경우 방문한 노드에 추가되지 않는다.
4단계에서 방문해야할 노드를 확인하였을 때, 앞으로 방문해야할 노드는 A가 된다. 하지만 이는 이미 방문한 노드가 된다. 그리하여 이때의 노드는 방문한 노드에 추가되지 않는다.
방문한 노드: ["A", "B", "C"]
방문해야할 노드: ["D", "E", "A", "F"]6. 방문해야할 노드가 없어질 때까지 작업을 진행
4단계와 5단계에서 했었던 방법을 참조하여 방문해야할 노드가 없어질 때까지 진행한다.
방문한 노드: ["A", "B", "C", "D"]
방문해야할 노드: ["E", "A", "F", "B"]
방문한 노드: ["A", "B", "C", "D", "E"]
방문해야할 노드: ["A", "F", "B", "B"]
방문한 노드: ["A", "B", "C", "D", "E"]
방문해야할 노드: ["F", "B", "B"]
방문한 노드: ["A", "B", "C", "D", "E", "F"]
방문해야할 노드: ["B", "B", "C"]
방문한 노드: ["A", "B", "C", "D", "E", "F"]
방문해야할 노드: ["B", "C"]
방문한 노드: ["A", "B", "C", "D", "E", "F"]
방문해야할 노드: ["C"]
방문한 노드: ["A", "B", "C", "D", "E", "F"]
방문해야할 노드: []