[백준] 2003 수들의 합 2

🌭 문제 설명

• N개의 수로 된 수열 A[1], A[2], …, A[N] 이 있다. 이 수열의 i번째 수부터 j번째 수까지의 합 A[i] + A[i+1] + … + A[j-1] + A[j]가 M이 되는 경우의 수를 구하는 프로그램을 작성하시오.

---

🍗 제한 사항

---

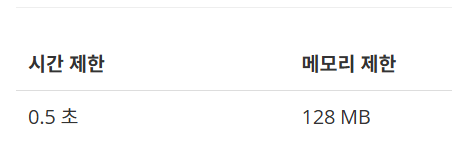
🎁 입출력 예시

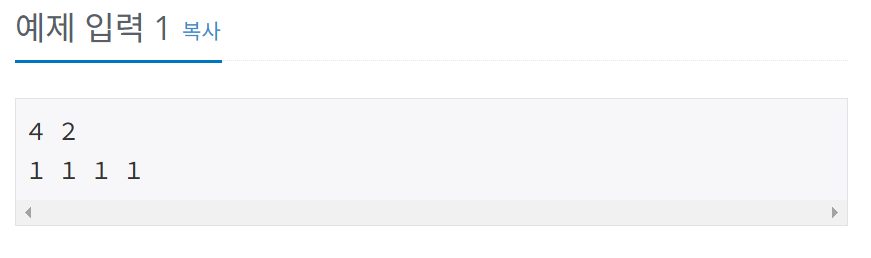
• 첫째 줄에 N(1 ≤ N ≤ 10,000), M(1 ≤ M ≤ 300,000,000)이 주어진다.
• 다음 줄에는 A[1], A[2], …, A[N]이 공백으로 분리되어 주어진다. 각각의 A[x]는 30,000을 넘지 않는 자연수이다.

• 첫째 줄에 경우의 수를 출력한다.

---

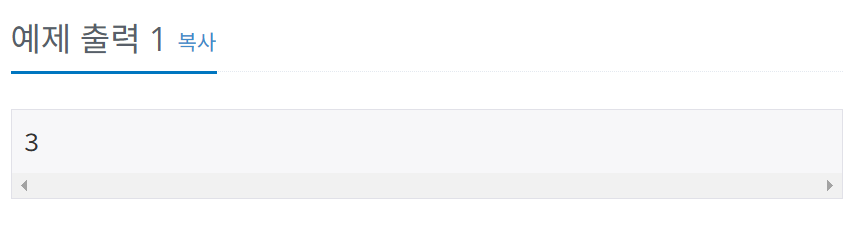
😎 나의 풀이

N, M = list(map(int, input().split()))
A = list(map(int, input().split()))

start = 0
end = 0
sum = A[0]

count = 0
while True:
  if sum == M:
    count += 1
  if sum >= M:
    start += 1
    sum -= A[start - 1]
  else:
    if end == N -1:
      break
    end += 1
    sum += A[end]
  
print(count)

1. 투 포인터 알고리즘을 이용해서 풀었다.
2. start 와 end , count 그리고 구간 합을 저장할 sum을 초기화 해준다. sum의 초기 값은 A의 0번 인덱스와 같기 때문에 A[0]으로 초기화
3. 구간 합 sum 이 M과 같으면 count를 1 더 해주고, sum이 M 보다 크거나 같으면 시작점인 start를 한칸 옮겨 주고 , A의 앞의 값을 구간합에서 빼준다.
4. sum이 M 보다 작으면 끝점인 end를 옮겨주고 sum에 구간합을 더해 준다.
5. end가 배열에 끝에 왔으면 break로 반복문 탈출

---

🧵 다른 풀이

N, M = map(int, input().split())
lst = list(map(int, input().split()))

end = 0
cnt = 0
summ = 0

for i in range(N):
	while summ < M and end < N:
		summ += lst[end]
		end += 1
	if summ == M:
		cnt += 1
	summ -= lst[i]

print(cnt)

1. 나랑 비슷한 투포인터 풀이가 가장 많았다.

---

• 투 포인터 알고리즘을 이번 기회에 제대로 알게 되었다.