데이터 과학 기초

Sampling (샘플 추출)

sample = 표본
population = 전체, 원본, 모집단
distribution = 분포

확률

전체가 100명일때 (릭과 모티 포함) 두 사람을 추출한다.

• 릭과 모티를 추출 안하는 확률

  • 98/100 * 97/99

• 릭과 모티 둘다 추출될 경우

  • (1/100)(1/99)+(1/100)(1/99)

몬티홀 문제

• 문을 옮기는 것이 확률이 더 높아

랜덤 추출 (Random Samples)

Deterministic sample(결정된 샘플)

• 확률이라는 개념이 없는 추출
  • 그냥 정해진 추출이라 생각하면 된다.

Random sample(랜덤 샘플)

• 표본을 추출하기 전에 모집단의 모든 그룹의 선택 확률을 알아야 한다.
  • 정확히 어떤 값이 얼마나 뽑히는지 알아야한다.
• 모든 개인/그룹이 선발될 수 있는 동등한 기회를 가질 필요는 없다.
  • 선택될 확률이 달라도 된다.

---

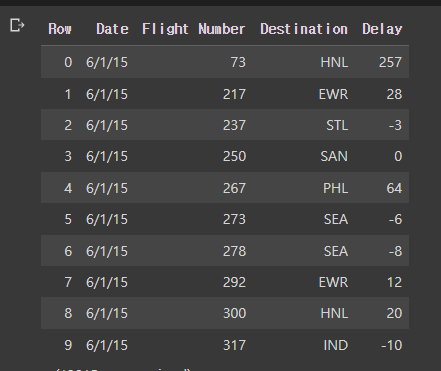
• 이러한 테이블이 있다

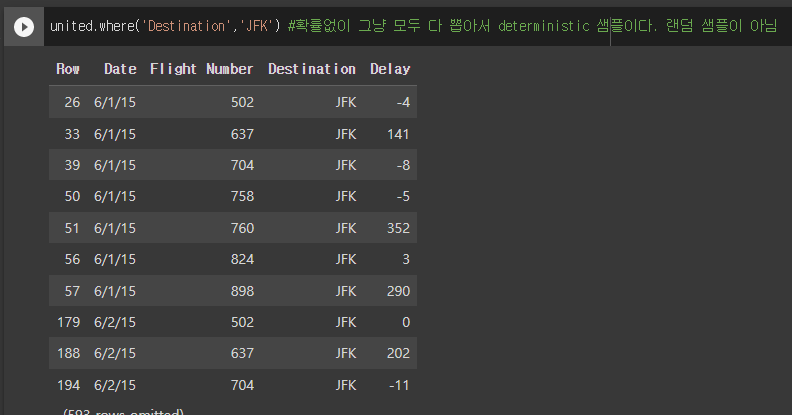
• 랜덤하게 값을 뽑는 것이 아닌, 특정한 값을 가지는 값들을 추출한다.
  • 그래서 deterministic sample이다.

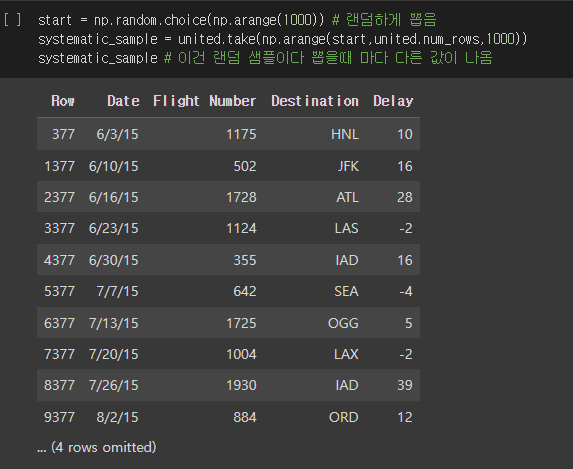
• 반면에 이는, 랜덤한 숫자를 뽑아 테이블에서 값을 추출한다
  • Random sample이다

Sample of Convenience 편리함의 표본

ex) 지나가는 사람을 대상으로한 추출

무작위로 표본을 추출했다고 해서 random sample을 추출한 것은 아니다.

• 미리 전체 polulation 얼마나되는지 알 수 없다면
• population에서 각 그룹이 선택될 경우, 확률을 모른다면

random sample이라고 할 수 없다.
그냥 편의상 랜덤 샘플이라고 하는 것이다.

distribution 분포

Probability Distribution 확률 분포

• 가능한 값이 정의된 다양한 값들??
  • 음.. 어떠한 값을 뽑을 수 있는 경우의 분포라 생각하자
• 확률 분포
  • 특정 양에 대한 가능한 값
    • 가능한 값이 정의가 되어야한다.
      • 특정 경우를 뽑는 경우의 값이 있어야 한다
        • ex) 안경을 낀, 안경을 안 낀
  • 각 값의 확률
    • 특정 값에 대한 확률이 정의되어야한다.
      • ex) 안경낀 학생을 고르는 경우는 1/6이다.
• 수학적으로 계산할 수 있다면, 시뮬레이션을 하지 않고 확률분포를 구할 수 있다.
• 그치만 시뮬레이션이 더 쉬운 경우가 있다.
  • 시뮬을 통해 생성된 distribution을 empirical distribution이라고 한다

Empirical Distribution 경험적 분포

(random sample 뽑기)실험을 토대로 나타낸 확률 분포

• Empirical: 관찰된 결과를 기반으로 한다.
• 관찰은 실험의 반복이다.
• 경험적 분포
  • 모든 값은 관찰마다 다른 값을 지닌다.
  • 각 값이 나타날때마다 비율이 정해진다..
    • 100 번했을 때 이 값이 몇번 나왔는가에 따라 비율이 정해진다

---

• 주사위가 가지는 값이다.
• 이걸로 주사위를 굴리겠다.

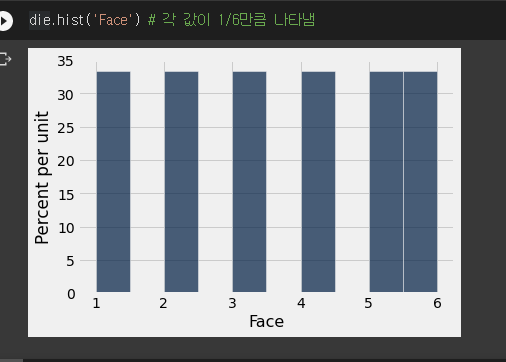
• 각 값은 1/6의 만큼 비율을 차지한다.

• 주사위에서 10번 무작위로 어떠한 값이 나왔는지 본다

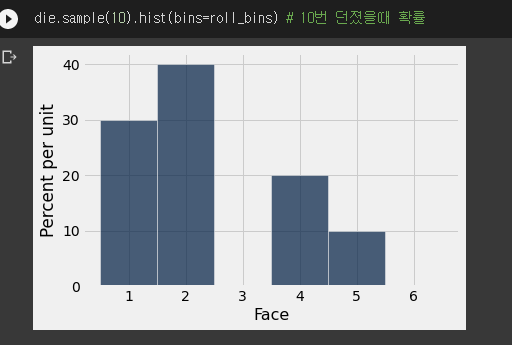
• 주사위를 10번 던졌을 때 각 값의 확률은 이렇게 나왔다.
  • 랜덤임

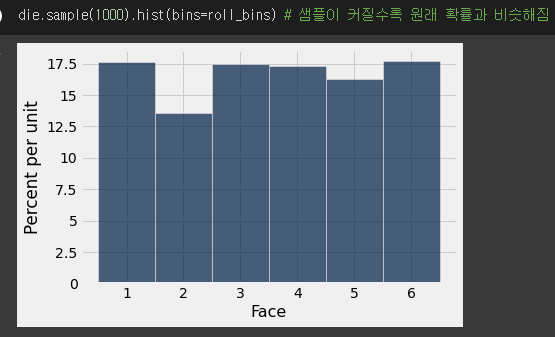
• 많은 실험을 할 수록 원래의 값과 비슷해진다.

• empirical distribution을 통해 진행했다...!!
  • 진행하는 횟수가 많을 수록 원래의 값과 비슷해지는 것을 발견했다!!

Large Random Samples

Law of Averages/ law of Large Numbers

우연한 실험이 여러 번, 독립적으로 그리고 동일한 조건에서 반복된다면 사건이 발생하는 시간의 비율은 사건의 이론적 확률에 더 가까워진다.

• 주사위를 굴리는 수를 늘리면 5가 나올 비율이 1/6에 가까워진다.

Empirical Distribution of a sample

표본 크기가 크면 균일한 랜덤 표본의 경험적 분포는 population의 분포와 유사하다.

• 샘플이 많으면 원래의 값과 같아진다.

---

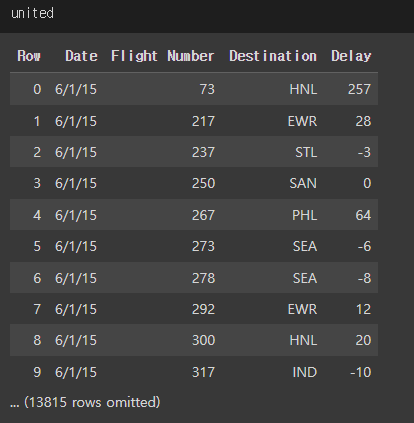
• 이런 테이블이 있다.

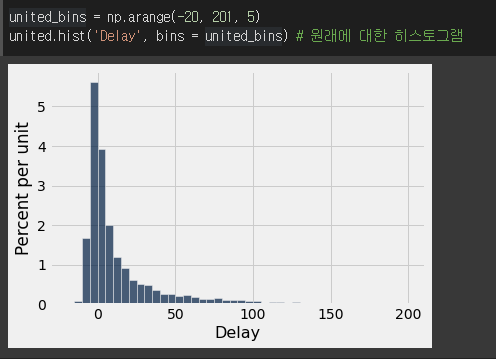
• 이 테이블 Delay 칼럼에 대한 히스토그램이다.

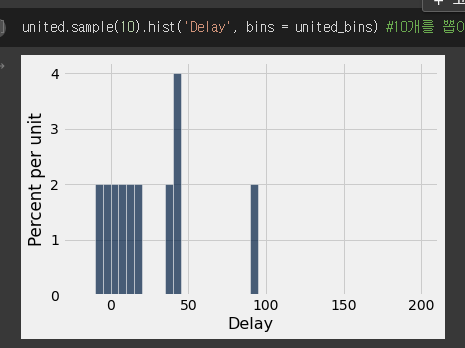
• 테이블에서 10개의 값을 랜덤하게 뽑아와서 히스토그램을 그려봤다.
  • 랜덤 샘플

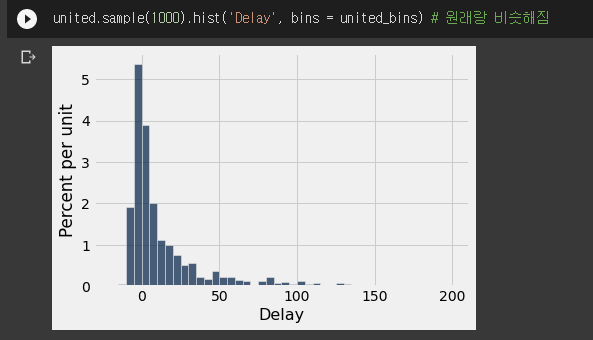
• 1000번 랜덤하게 뽑으니 원래의 값과 비슷해졌다..
  • large random samples.. law of average에 따라 샘플의 크기가 크니 원래의 값과 비슷해졌다

Statics 통계치

추론

Statistical Inference 통계적 추론

• 랜덤 표본의 데이터를 기반으로 결론을 내린다.

ex)

• 데이터를 사용하여 알수 없는(고정된,평균의) 숫자의 값을 예측한다.
• random sample을 근거로 알 수 없는 양에 대한 값을 추정

용어

Parameter

• population에 대해 계산된 값이다.

Statistic

• 샘플에 대해 계산된 값이다.

Statistic은 Parameter의 추정치로 사용할 수 있다.

---

• Large Random Samples에서 사용한 테이블이다.

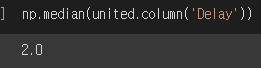
• Parameter이다.

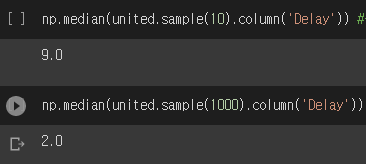
• statistic이다.
• 샘플을 많이할 수록 parameter와 가까워지는 것을 볼 수 있다.
  • 물론 이 값들도 다 랜덤이다
    • 랜덤이지만 값들이 parameter와 가깝다는 것을 뜻한다.

Probability Distribution of a statistic 통계의 확률 분포

그냥 통계치의 값은 다양하다 라는 걸 의미

• 통계의 값은 다양하다

  • 랜덤 표본이 달라지기 때문이다.
    • 샘플이 계속 바뀌니...

• 통계의 "표본 분포" 또는 "확률 분포":

  • 통계의 모든 가능한 값과 이에 상응하는 모든 확률값이 있다.
  • 샘플링을 할때마다 나오는 값들에 대해서 분포를 만들 수 있다.

• 어떻게 구하는가

  • 수학적으로 계산을 하거나
    • 너무 경우가 많아!
  • 표본(샘플)을 생성하고 각 표본을 기반으로 통계를 계산해야 한다.

Empirical Distribution of a statistic 통계의 경험적 분포

그럼 통계치를 여러번 구해서(경험적 분포)그래서 확률 분포를 만들 수 있다

• 통계량의 경험적 분포

  • 통계의 시뮬레이션된 값을 기반으로
  • 통계의 모든 관측값으로 구성
  • 각 값이 나타난 횟수의 비율로
    • 값이 얼마나 자주 나오는가에 따라서

• 시뮬레이션의 반복 횟수가 클 경우 statistic의 확률분포에 가까워 진다

  • 많이 시뮬을 할 경우에 그 값들이 나오는 비율을 모아 분포를 만들 수 있다

---

앞에서 사용한 테이블을 그대로 사용하겠다.

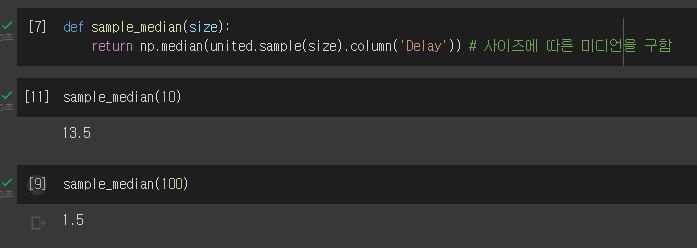
• 테이블 Delay 칼럼에서 중간값을 뽑는 함수를 생성했다.
  • 샘플을 뽑아서 중간값을 계산한다.

population 대해서는 값이 2.0이었다.

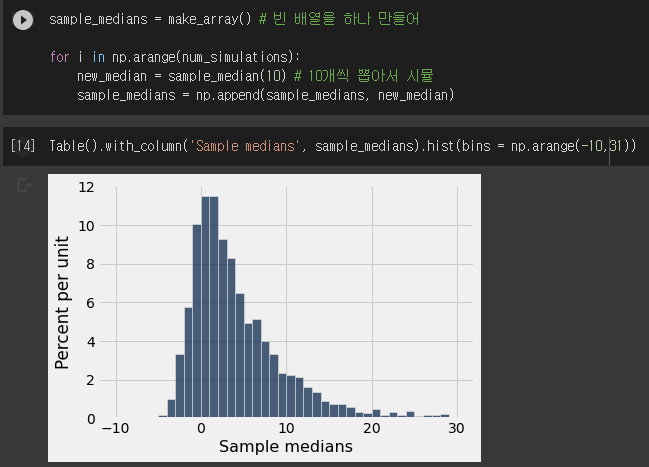
• 10개씩 뽑아 중간값을 구하는 통계를 2000번 반복해 히스토그램(경험적분포로 만든 확률분포)을 그렸다.
  • 2에 가까운 값의 분포가 젤 많다,

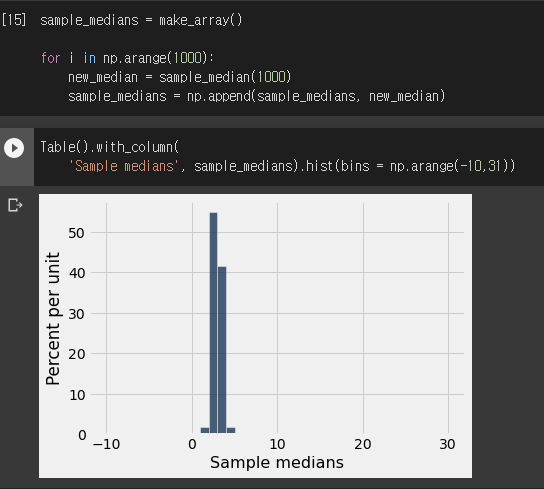
• 1000개씩 뽑아 1000번 시뮬레이션을 했다.
  • 더욱 가까운 분포를 그린다.

모델

• 모델은 데이터에 대한 가정의 집합이다.
  • 데이터는 어떠할 것이다! 라는 가정
• 데이터 과학에서 많은 모델은 랜덤성을 포함하는 프로세스에 대한 가정을 포함한다.
  • Chance model이라고 한다.
    • 랜덤성이 있기 때문에

주요 관점: 모델이 데이터에 적합한가?

Approach to Assessment 모델 평가 방법

• 모델의 가정에 따라 데이터를 시뮬레이션할 수 있다면 모델을 통해 예측할 수 있다.
  • 그런 다음 예측을 데이터와 비교할 수 있다.
• 데이터와 모델의 예측이 일치하지 않으면 모델은 잘못 되었다는 것을 뜻한다.

한번 모델을 통해 예측해보자

categorical 범주에서 무작위 추출을 한다.

sample_proportions(샘플 크기,비율)

• 모집단에서 랜덤하게 샘플을 추출한다.
  • 샘플에 있는 범주의 empirical 분포를 포함하는 배열을 반환한다.

이게 무슨 함수지..? 할 수 있다...

한번 실행 해보자

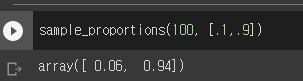
• 일단 0.1과 0.9의 비율을 가지는 값을 100번 추출해봤다.
  • 저러한 결과가 나왔다

그럼 한번 10000번 추출해보자

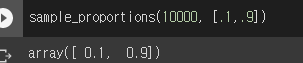
• 오호...

그래서 sample_proportions는 해당 비율을 주면 이를 주어진 횟수만큼 샘플링해준다고 할 수 있다.

1. 문제를 파악
2. population에서 샘플했을 때에 비율을 구해
3. 현재 나타나는 문제의 비율을 구해
4. 이를 비교해봐

한번 5퍼센트 안에 오는지 체크 해보자 낼
오 된다