데이터 과학 기초

Testing Hypothesis

observed statistic: 모집단으로 부터 관측된 값

Model and Alternative 모델 및 대안

배심원 문제

• 모델
  • 배심원들은 랜덤하게 구성되었다.
• 대안 관점
  • 아니다 흑인에 대한 편견이 있다.

유전 문제

• 모델
  • 각 식물은 75퍼센트의 확률로 보라 꽃을 피운다.
• 대안 관점
  • 아니다

모델을 평가하는 단계

모델이 불일치하는가? 를 판단하기 위해서

1. 모형과 데이터 사이의 차이를 측정할 통계치를 선택
2. 모형의 가정에 의해 통계 시뮬레이션을 한다.
3. 실제 데이터를 모형의 예측 통계치와 비교한다.
   • 히스토그램 그리기
     • 히스토그램안에 observed statistic이 어디있느냐를 본다

observed statistic이 히스토그램에서 멀리 떨어져 있으면 모형이 잘못 되었다는 것이다.

관점에 대한 접근

관점에 따라 통계를 어떻게 측정할 것인지 나뉘어진다.
아래 A와 B는 서로 다른 주장을 한다.

상황 : 동전을 400번 던진 결과에 대해.. 의견이 나뉜다.

A. 동전을 던지는데 한쪽만 나온다.

• 의견: 코인은 공정하게 던져진다.
  • 이를 검증하기 위해선 앞이 나올 확률, 뒤가 나올 확률 모두 계산해야한다.
    • 왜냐면 어떠한 면이 나오는 것이 치중되었는지 모르기 때문
• 의견: 아니다.

B. 동전을 던지는데 앞면만 나온다.

• 의견: 코인은 공정하게 던져진다.
  • 이름 검증하려면 앞면의 확률만 계산하면 된다.
• 의견: 아니다, 앞면만 나온다.

statistic을 앞면이 나오는 비율로 정했을 때,
A와 B에 대해서 앞면의 비율이 50퍼로 측정되면 공정하다 할 수 있다.

A

• 앞면의 비율이 너무 크거나 너무 작으면 공정하지 않다고 할 수 있다.
  • 앞면의 비율이 크다 = 앞면에 치중
  • 앞면의 비율이 작다 = 뒷면에 치중
  • 50%와 앞면의 비율 사이의 차이가 key이다
    • 통계치 = |앞면의 비율 - 50|
      • 통계치값이 크면 공정하지 않다..

B

• 앞면의 비율이 크면 앞면에 치우쳤다는 것을 의미한다.
  • 통계치 = 앞면의 비율
    • 이 통계치가 큰지 살펴본다

Comparing Distributions 분포 비교

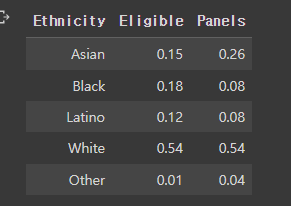
• 이러한 테이블이 있다.

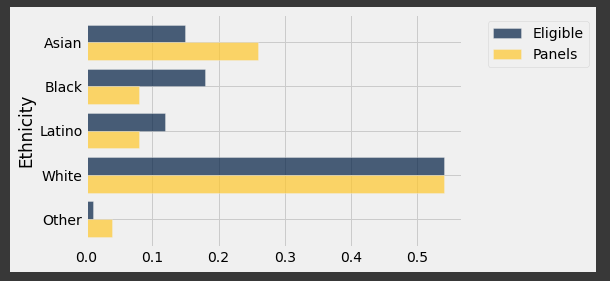
• 아시안은 원래 비율보다 많고 흑인과 라틴은 비율보다 적다.
• 이러한 결과가 나오는지 시뮬레이션 해보자

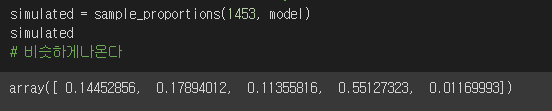
• 비슷하게 나온다.

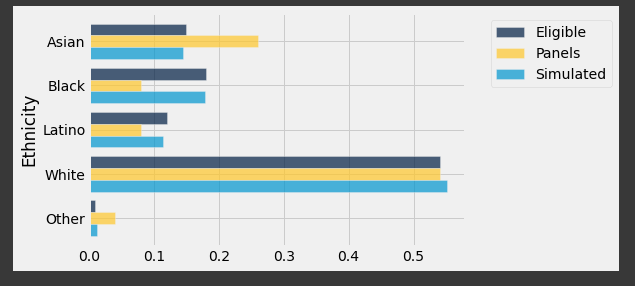
• 그래프를 그리면 이러하다.

New Statistic

그렇다면 여러가지 범주가 있을 때는 statistic을 어떻게 정할 것인가?
원래는 하나의 범주에 대해서만 통계치를 설정했으면 되었다. 하지만 여러 값이 있다면 이 범주의 차이를 이용해 통계치를 설정해야할 것 같다.. 한번 알아보자

지금 패널과 패널 적격의 차이를 이용해 통계치를 정하려고 한다 이때 쓰는 값에 대해 알아보는거임!!

Distance between distributions

위의 테이블에서

• 패널에 있는 사람들은 여러 민족을 가지고 있다.
• 민족 분포는 categorical이다.
• 패널들의 민족 분포가 eligible 배심원들의 민족 분포와 가까운지 확인하기 위해, 두 범주 분포 사이의 차이를 측정해야 한다.

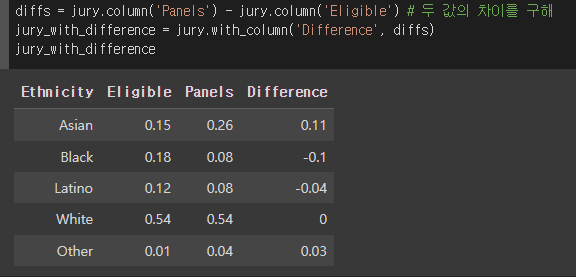
• Panel과 Eligible의 차이를 측정했다.

Total Variation Distance 총 변동 거리

각 차이에 맞는 계산법이 있다.

Total Variation Distance TVD

1. 각 카테고리 값에 대해 두 비율의 차이를 구한다.(배열에 각 카테고리 값에 대한 차이가 있음)
2. 1의 값의 절대값을 구한다.
3. 2의 배열 값을 다 더해 2로 나눈다.

• tvd를 구하는 함수이다.

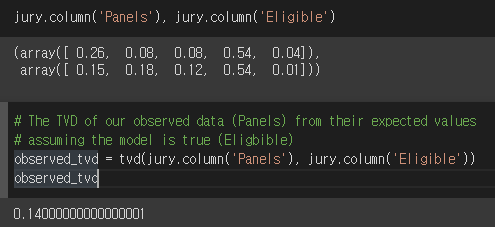
• 테이블의 해당 칼럼에 대해 tvd를 구해보겠다
  • categorical한 값에 대해
  • 이 tvd는 관측된 데이터에 의한 tvd이다.

이제 모델을 시뮬레이션해 tvd를 구해보자

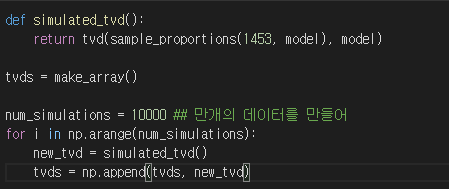
• 10000번 시뮬레이션해 시뮬레이션 마다 tvd를 구하였다.

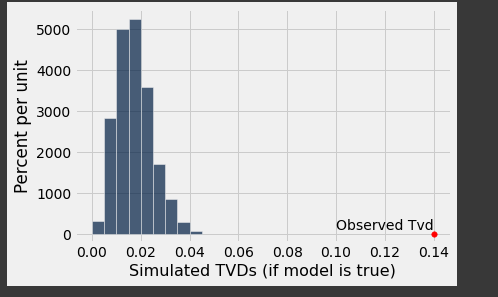
• 이를 히스토그램으로 나타내고, 관찰된 데이터의 tvd를 점으로 찍어보았다.
  • 차이가 정말 많이 난다.
• 시뮬레이션의 분포와 관찰된 statistic의 차이가 정말 많이 난다.

모델에 근거한 분포의 값과 실제의 값의 차이가 많이나는 것으로 보아 모델은 잘못되었다

요약

categorical 분포에서 랜덤하게 표본을 추출했는지 여부를 평가하려면:

• TVD는 두개의 categorical 분포 간의 거리를 통계치로 사용하기 위해 사용한다,
• population에서 무작위로 표본을 추출하고 무작위 표본에서 TVD를 계산한다.
  • 여러 번 반복한다.
    • 즉, 여러번 모집단에서 여러번 관찰을 하고 이 각각의 관찰 값에 대한 tvd를 계산해라란 뜻이다
• 밑의 두 값을 비교해 랜덤한지의 여부를 판단하자
  • 시뮬레이션 TVD에 대한 empirical distribution과
  • observed된 실제 TVD를 비교

Testing Hypotheses 가설 검증

• 현재 데이터가 어떻게 생성되었는지 두가지 관점(가설)으로 볼 수 있다.
  • null
  • alternative
• 그 관점들을 가설이라고 한다.
• 관측된 데이터를 통해 제일 좋은 가설을 선택한다.

Null and Alternative

Null 가설

• 데이터가 생성되는 방식에 대해 잘 정의된 chance 모델
  • 모델이 데이터와 일치한다.
• 이 모델 가정에 의해 데이터를 시뮬레이션할 수 있다.

Alternative 가설

• null 가설과 반대되는 가설
  • 모델이 데이터와 일치하지 않는다.

Test Statistic

• 두 가설 중 무엇이 맞는지 알기 위해 정의하는 통계치

통계치를 선택 전 고려해야하는 점

• 통계의 어떤 값들이 null 가설로 기울게 만들 것인가?
• 어떤 값들이 alternative 쪽으로 기울게 만들 것인가?
  • 특정한 값이 높으면 alternative라고 가정해라

Prediction under null hypothesis

null 가설에 따라 test statistic을 시뮬레이션하고 시뮬레이션된 값의 히스토그램을 그린다

• null 가설 하의 통계의 empirical 분포이다.
• 시뮬레이션을 한 결과!

null 가설에 의해 만들어진 통계에 대한 예측이다.

• 통계의 가능한 모든 값을 표시한.
• 확률(null 가설이 참인 경우)도 표시돤다.

가능한 랜덤 표본을 모두 생성할 수 없기 때문에 확률은 근사치로 나타난다.

Conclusion of the Test

null 가설과 alternative 가설 사이의 선택

• observed test statistic과 null가설에 따른 empirical distribution을 비교한다.
• 관측된 값이 분포와 일치하지 않으면 alternative를 증명하는 것이다
  • 데이터가 alternative와 더 일치한다

값이 분포와 일치하는지 여부:

• 시각화만으로도 충분할 수 있다.
• 그렇지 않은 경우 "일관성"에 대한 규칙이 있다.

---

한번 해보자!

Statistical Significance

얼마나 통계적으로 의미가 있는가?

Tail Areas

시뮬레이션된 분포와 관측된 값이 얼마나 먼가

• 시뮬레이션 된 분포의 꼬리에서부터 측정한다

Conventions About Inconsistency

null가설과 불일치

• test statistic이 null 가설에 따라 얻은 분포 값의 꼬리 부분에 얼마나 있는가에 따라서

• 꼬리의 면적이 5% 미만일 때

  • inconsist하다
  • 통계적으로 의미가 있다 정도

• 꼬리의 면적이 1% 미만일 때

  • inconsist하다
  • 통계적으로 매우 의미가 있다 정도

불일치 확인 방법

P value 계산법

• 분포의 영역이 관찰된 값보다 멀리 있는 확률

• 시뮬레이션한 statistic의 값이 관찰된 값보다 얼마나 있는지 파악 후 이를 퍼센트로 나타낸다.

개수/시뮬 횟수 * 100

ex)

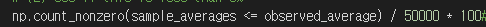
• 시뮬레이션한 값이 관찰 값보다 작은 경우가 몇개인지 센 후
• 이를 전체 시뮬한 개수에 나눠 퍼센트를 구한다.

시뮬레이션한 statistic 값 중 n퍼센트에 해당하는 값과 관찰 값을 비교한다.

• 해당 값이 관찰 값보다 작으면 꼬리의 면적이 5퍼센트보다 크다는 것을 의미한다.

여기선 5퍼센트로 정하였다.

ex)

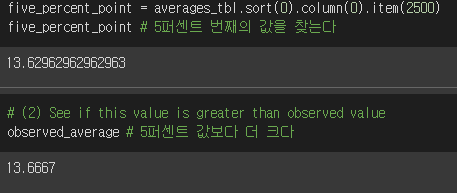
• 총 50000번 시뮬했으니 2500번째가 5퍼센트를 의미한다.

  • 값을 소팅해 2500번째 값을 선택해 비교를 하자!

시각적으로 해결한다.

• 시뮬레이션한 statistic의 확률분포 히스토그램에서 관찰된 값을 찍어보자

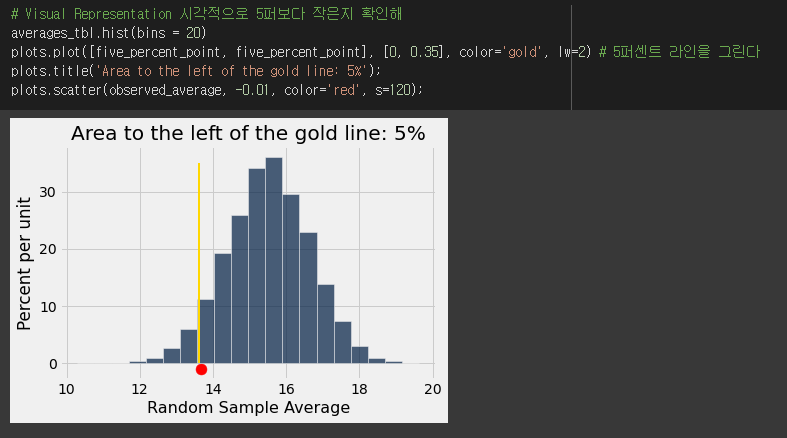
• 5퍼센트에 해당되는 값을 찾아 이를 그림에 그리자

Definition of the P value

정식 이름: observed significance level

P-value

• null 가설 하에서 test statistic이 시뮬레이션한 값과 같거나 alternative 방향으로 갈때의 확률 값
  • alternative 방향
    • 크다면 큰 방향으로
    • 작다면 작은 방향으로

걍 이게 얼마나 속하냐 확률값 ㅇㅇ