• https://www.geeksforgeeks.org/red-black-tree-set-1-introduction-2/

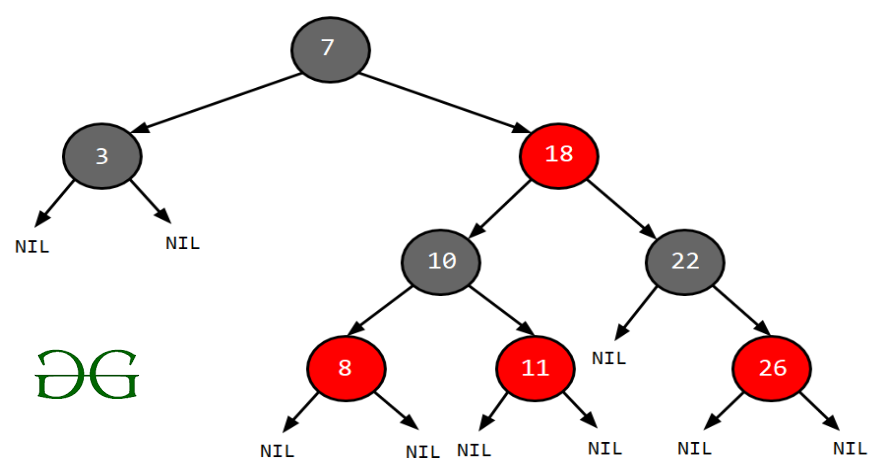
BST

• binary search tree
• 이진 탐색 트리
• 이진탐색의 장점과 연결리스트의 장점을 결합
• 나를 기준으로 왼쪽 subtree는 나보다 모두 작은 값이어야 하고 오른쪽 subtree는 모두 큰 값이어야 함

Red-Black Tree

• balanced BST의 일종.
• 일정한 규칙에 따라 트리를 balance하게 유지.
• BST는 복잡도가 트리의 height에 따라 O(n)
• Red-Black Tree는 트리의 높이를 log n 으로 일정하게 유지하여 SEARCH, INSERT, DELETE와 같은 작업이 O(log n) 이 되게끔 한다. (n은 노드의 개수)

Red-Black Tree의 규칙

1. Root Property : root node는 Black
2. External Property : 모든 external node는 Black
3. Internal Property : Red 노드의 자식은 모두 Black
4. Depth Property : 모든 leaf node에서 root 노드까지 Black 노드의 개수는 같다.

AVL Tree와 비교

• AVL tree는 RB tree에 비해 균형이 더 잘 잡혀 있지만 insertion과 deletion에서 더 많은 rotation이 발생할 수 있음. (avl tree는 높이 차이가 1보다 커지면 rotation 시켜서 균형 유지)
• 따라서 빈번한 삽입 삭제가 발생하는 경우 Red-Black tree가 더 낫다. (삽입 삭제 할 땐 규칙이 덜 빡센 Red Black tree가 더 빠를 수 있기 때문에)
• 대신 삽입 삭제보다 검색이 더 빈번한 작업이라면 AVL tree가 더 나음 (검색은 균형이 더 잘 잡힌 AVL tree가 더 빠를 수 있기 때문에)

ex)

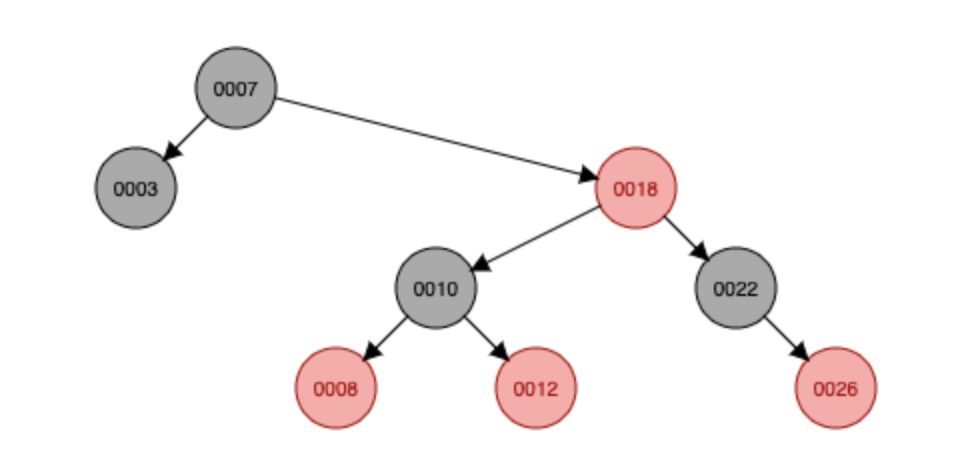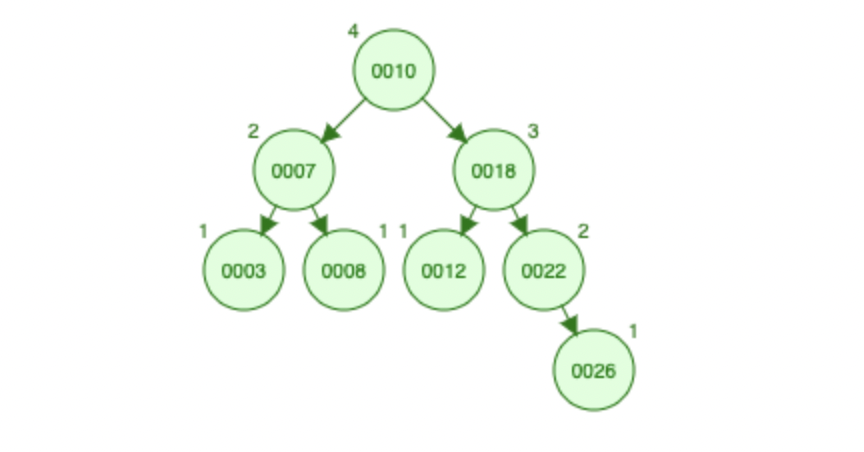Red-Black tree O(log n) 증명

• https://iq.opengenus.org/time-and-space-complexity-of-red-black-tree/
• Red-Black tree의 규칙(모든 leaf node까지의 black node 개수는 같다)에 의해 black depth는 $O(\log{n_b})$ (nb는 black node의 개수)
• black depth가 $O(\log{n_b})$ 로 제한일 때, 전체 tree height의 최악의 시나리오는
  (black-red-black-red-..-red-black)
• 즉 $O(2\log{n_b})$
• 즉 Red-Black tree의 height의 복잡도는 $O(\log{n})$

Red-Black tree 연습해보기

• https://www.cs.usfca.edu/~galles/visualization/RedBlack.html

Insertion & Insertion fix

• https://zeddios.tistory.com/237

0. 삽입되는 노드는 모두 Red 노드이다.
1. 삽입된 노드의 uncle이 Red인 경우 -> Recoloring
   1-1. parent와 uncle을 Black으로 바꾸고 grand parent를 Red로 바꾼다.
2. 삽입된 노드의 uncle이 Black인 경우 -> Restructuring
   2-1. 나, parent, grandparent의 중간 값을 구한다.
   2-2. 중간 값이 parent자리에 가고, 나머지 값이 중간 값의 왼쪽 오른쪽 child가 되게 rotate한다.
   2-3. parent를 Black으로 설정하고 나머지 두 자식을 Red로 설정한다.

• Recoloroing의 경우 한 번으로 끝나지 않을 수 있다. grand parent의 parent가 Red였을 경우, Recoloring 이후 또 double red가 발생하게 되기 때문에 다시 케이스에 따라 Recoloring 또는 Restructuring을 해준다.
• Restructuring의 경우 한 번에 끝나게 된다. 새로 삽입한 노드의 parent의 서브트리 모양을 바꾸게 되는 건데, parent를 Black으로 만들고 서브트리는 규칙에 맞게 Restructuring 되는 것이기 때문에 double red가 발생하지 않는다.

Deletion

• https://www.youtube.com/watch?v=6drLl777k-E

0. 트리에서 노드를 삭제할 때 없어지는 색을 y_origin_color 라고 한다. 이 origin_color에 따라 fix up 여부가 달라짐. (origin_color가 Black일 때만 fix up이 필요하다. -> 이 때만 Black height이 달라지므로.)

1. 삭제하려는 노드를 z라고 할 때
   1-1. z의 자식이 두 명이 아니라면 없어지는 y_color는 z color.
   존재하는 z의 자식(둘 다 존재하지 않는다면 leaf node)를 z 자리에 이식. z는 해제
   1-2. z의 자식이 두 명이라면 없어지는 y_color는 minimum(z->right) color.
   minimum(z->right)을 z자리에 이식하기 때문에 결국 사라지는 색은 minimum의 색. (z 자리에 이식할 때 노드색을 z 것으로 물려받는다.)

2. fix up에 사용할 노드를 x라고 할 때
   2-1. z의 왼쪽 자식이 없다면 x는 z->right. z의 오른쪽 자식이 없다면 x는 z->left.
   2-2. z의 자식이 두 명이라면 x는 minimum(z->right)->right.
   minimum은 subtree의 가장 왼쪽 노드이므로 왼쪽 자식이 없음. right가 당연함.

Deletion fix

Case 4. s는 Black. s->right가 Red.

1. s의 color = s->parent color.
2. s->parent, s->right color = Black.
3. s를 기준으로 rotate.

Case 3. s는 Black. s->left는 Red. s->right는 Black.
s->right를 Red가 되게 만든 다음 Case4를 적용한다.

1. s와 s->left의 color를 바꾼다. (s는 Red로, s->left는 Black으로 바뀜)
2. s->parent를 기준으로 right rotate. (s->parent, 즉 Red가 right child가 된다.)

Case 2. s는 Black. s->left도 Black. s->right도 Black.
s를 Red로 바꾸고 x->parent에 fix up을 위임. (x = x->parent로 한 다음 다시 x->parent 입장에서 fix up 진행.)

1. s->color = Red
2. x = x->parent
이후 Case 1, Case 2, Case 3, Case 4를 업데이트된 x 입장에서 다시 검사하여 fix up 진행

Case 1. s가 Red. s를 Black으로 바꾼 다음 Case 2, Case 3, Case 4를 검사.

1. s->color = Black
Case 2, Case 3, Case 4 (s가 Black인 케이스들) 차례로 검사하면서 fix up 진행

구현 설명

• https://gowoonsori.com/data-structure/tree/redblacktree/ 👍
• https://code-lab1.tistory.com/62 👍
• https://eat2go.tistory.com/37 👍
• https://zeddios.tistory.com/237 👍👍👍