✏️ 문제
세 명의 수포자가 각자 자신만의 특정한 순서에 따라 문제의 정답을 찍으면
누가 더 많은 문제를 맞혔는지 알아내기

🧩 풀이
첫 번째 시도 : 시간복잡도 O(n)
- 수포자 1,2,3의 점수를 기록하기 위해 answer_one, answer_two, answer_three 변수에 기록
- answers 배열의 각 요소를 순차적으로 확인하며, 각 수포자의 답안 패턴과 비교
- 각 수포자가 맞힌 문제의 개수에 따라 answer_one,two,three 값을 증가시킴
- 조건문을 통해 각 수포자의 점수를 비교하여, 해당 수포자가 다른 수포자보다
높은 점수를 가진 경우 그 수포자의 번호를 answer 리스트에 추가
def solution(answers) :
one = [1, 2, 3, 4, 5]
two = [2, 1, 2, 3, 2]
three = [3, 3, 1, 1, 2]
answer_one=0
answer_two=0
answer_three=0
answer=[]
for i in range(len(answers)) :
if one[i] == answers[i] :
answer_one += 1
elif two[i] == answers[i] :
answer_two += 1
elif three[i] == answers[i] :
answer_three += 1
if (answer_one > answer_two) or (answer_one > answer_three):
answer.append(1)
if (answer_two > answer_one) or (answer_two > answer_three) :
answer.append(2)
if (answer_three > answer_one) or (answer_three > answer_two) :
answer.append(3)
return answer
두 번째 시도 : 시간복잡도 O(n^2)
- answer 배열을 순회하면서 pop(i)를 사용해 수포자의 패턴에서
i번째 요소를 제거하면서 해당 값이 answer[i]와 일치하는지 확인
- 패턴의 답이 맞으면 answer 리스트에 해당 수포자의 번호(1,2,3 중 하나)를 추가
- 리스트가 비어 pop을 사용할 수 없어 오류가 발생하면 프로그램이 멈추지 않도록 try-except블록 사용
- answer 리스트에 추가된 수포자의 번호들을 중복 없이 리스트로 반환
def solution(answers) :
answer = []
one = [1, 2, 3, 4, 5]
two = [2, 1, 2, 3, 2]
three = [3, 3, 1, 1, 2]
try :
for i in range(len(answers)) :
if one.pop(i) == answers[i]:
answer.append(1)
if two.pop(i) == answers[i]:
answer.append(2)
if three.pop(i) == answer[i] :
answer.append(3)
else :
pass
except :
pass
return list(set(answer))
세 번째 시도 : 시간복잡도 O(n)
- 수포자의 맞힌 문제 수를 기록하기 위해 score 리스트 생성 후 초기화
- answers를 순회하면서 각 수포자의 패턴과 주어진 정답을 비교
- 수포자가 정답을 맞히면, 해당 수포자의 점수를 score 리스트에 증가시킴
- max_score를 사용하여 score리스트에서 가장 높은 점수를 찾기
- score 리스트를 순회하면서 각 수포자의 점수가 max_score와 같으면
그 수포자의 번호(1,2,3)를 result 리스트에 추가하여 반환
def solution(answers) :
one = [1, 2, 3, 4, 5]
two = [2, 1, 2, 3, 2, 4, 2, 5]
three = [3, 3, 1, 1, 2, 2, 4, 4, 5, 5]
score = [0, 0, 0]
for i in range(len(answers)):
if answers[i] == one[i] :
score[0] +=1
if answers[i] == two[i] :
score[1] +=1
if answers[i] == three[i] :
score[2] +=1
result = []
max_score = max(score)
for i in range(3) :
if score[i] == max_score :
result.append(i+1)
return result
❗️ 결과
첫 번째 시도 결과
- one, two, three 배열은 모두 짧은 길이를 가지며, answer 배열의 길이가 더 길 경우 인덱스 에러가 발생
- elif 대신 if를 사용해서 모든 조건을 독립적으로 처리
- 수포자 간 점수 비교를 제대로 수행하지 않아 모든 수포자가 추가 될 가능성이 있음
- 결정적으로, 오답일 뿐더러 런타임 에러 발생
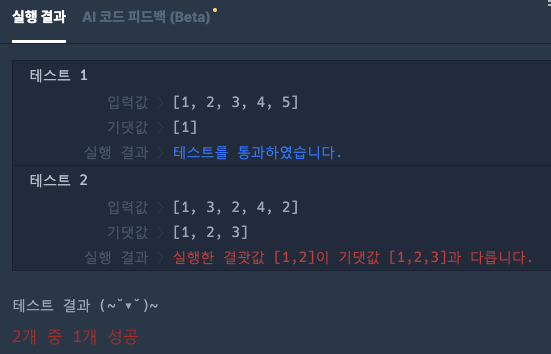
두 번째 시도 결과
- 메모리 절약하기 위해 pop 메소드 이용하려고 했지만 리스트의 길이를 줄이고,
결과적으로 다음 인덱스의 요소에 접근할 대 문제가 발생하며, 답안 패턴이 유지되지 않음!!
- 오류가 발생하는 부분을 try-except로 대비했지만 오류를 감추는 것 밖에 안됐음
- 각 수포자가 맞힌 문제의 개수를 확인하고, 최고 점수를 가진 수포자들을 반환하는 논리가 잘못됨
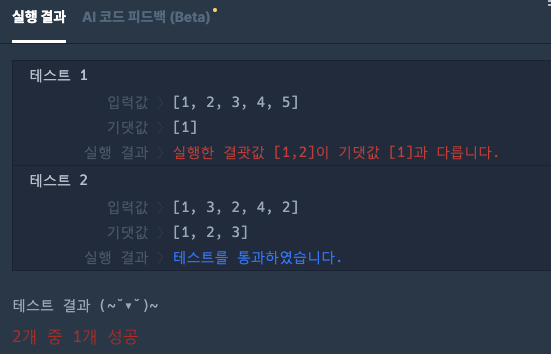
세 번째 시도 결과
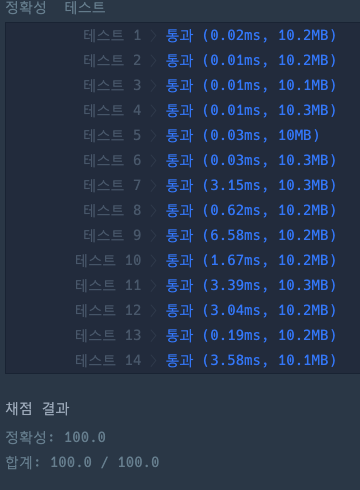
💡회고
- 잘했던 점
횟수가 3번밖에 되지 않지만 시간은 1시간이 넘도록 시도했었다.
포기하지 않고 내가 생각해낼 수 있는 것들은 다 생각하면서 시도했다.
결국 마지막엔 GPT의 힘을 조금 빌렸지만, 접근 방식은 아예 다른길이 아니라 다행이다.
- 고쳐야 할 점
너무 쉽게 가려고 하지 말고 일단 구현하는 것을 목적으로 두는 것이 좋겠다.
코테 스터디 처음에는 쉬운것도 어렵게 생각해서 함수부터 생각하기로 했었는데..
역시 많은 문제를 풀어봐야 내가 아는 것이 많아지는 것 같다.
항상 GPT의 힘을 빌리면 아예 모르는 것이 아니었는데, 내가 할 수 있을 것 같았는데,
너무 어렵고 답답한 마음에 물어보면 답이 간단해서 황당했던 적이 많았다.
오늘처럼 끝까지 포기하지 않고 계속 시도해보며 잘못된 부분을 깨닫고 고치는 것이 좋겠다.
- 새롭게 알게된 점
✔️ 완전탐색
- 가능한 모든 경우의 수를 전부 탐색하여 답을 찾는 방법
- 시간복잡도가 높을 수 있음
- 경우의 수가 많아지면 비효율적일 수 있지만, 정답을 보장할 수 있음
(모든 가능성을 탐색하기 때문에)
✔️ 장점
- 다양한 문제에 적용 가능
- 모든 경우를 다 체크하기 때문에 정확성이 높음
✔️ 단점
- 복잡도가 높아져서 실행 시간이 매우 길어질 수 있음
- 입력 크기가 커지면 현실적으로 사용하기 어려움
✔️ 활용부문
- 모든 조합을 찾아야 할 때 (n개의 아이템에서 k개를 선택)
- 최적의 해를 찾아야 할 때 (다른 알고리즘이 없거나 생각이 안날 때)
- 입력 크기가 작아서 모든 경우의 수를 다 탐색해도 무방할 때
✔️ 단순한 완전탐색 예제
- 1부터 100까지 모든 숫자를 탐색하여 특정 조건을 만족하는 숫자 찾기
for i in range(1,101):
if i가 조건을 만족하는지 확인 :
print(i)
✔️ 조합을 이용한 완전탐색 예제
- 4개의 원소에서 2개를 뽑는 모든 조합 생성
from itertools import combinations
items = ['a','b','c','d']
for combo in combinations(items,2):
print(combo)
('a', 'b')
('a', 'c')
('a', 'd')
('b', 'c')
('b', 'd')
('c', 'd')





