역시 문제를 잘 이해해야하는군요
문제에서 주어진 조건의 특성을 아주 잘 이해해야합니다.
이 문제에서 요구하는 기대값은 시작 정점과 도넛 형태 그래프의 수 , 막대 형태 그래프의 수, 8형태 그래프의 수 이다.
이 문제에선 여러 간선들만이 입력으로 주어지는데 따라서 간선들만으로 답을 유도해야 합니다.
상호 베타적 집합 (Union Find)
시작 정점 구하기
문제에선 다음과 같이 조건을 추가했습니다.
도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프의 수의 합은 2이상입니다.
따라서 간선들을 종합해 indegree 가 0 이고 outdegree 가 2 개 이상인 정점이 시작 정점입니다.
indegree : 현재 정점으로 들어오는 간선의 수
outdegree : 현재 정점에서 나가는 간선의 수
int startVertex = -1;
int[] ods = new int[1000005];
int[] ids = new int[1000005];
{
for (int[] e : edges) {
int od = e[0];
int id = e[1];
ods[od]++;
ids[id]++;
}
for (int i = 0; i < 1000005; i++) {
if (ods[i] > 1 && ids[i] == 0) startVertex = i;
}
}그래프 수 구하기
기본적으로 그래프들은 간선으로 이어져있기에 간선을 통해 정점들을 union 해준 뒤 HashMap 을 통해 각 집합 별 정점의 수와 간선의 수를 저장하여 그래프의 수를 구합니다.
int[] unionArr= new int[1000005];
{
for (int i = 0; i < 1000005; i++) {
unionArr[i] = i;
}
for (int[] e : edges) {
int od = e[0];
int id = e[1];
if (od == startVertex) continue;
union(od, id, unionArr);
}
}
public static int find(int n, int[] unionArr) {
if (unionArr[n] == n) return n;
return find(unionArr[n], unionArr);
}
public static void union(int a, int b, int[] unionArr) {
int aR = find(a, unionArr);
int bR = find(b, unionArr);
if (aR == bR) return;
unionArr[aR] =bR;
}그래프 별 정점의 수와 간선의 수는 다음 관계를 따릅니다.
도넛 그래프 = (정점 수 - 간선 수) = 0
막대 그래프 = (정점 수 - 간선 수) > 0
8 그래프 = (정점 수 - 간선 수) < 0
class Info {
public Set<Integer> set; // 정점들
public Integer cnt; // 간선의 수
public Info() {
set = new HashSet<>();
cnt = 0;
};
}
int[] answer = {startVertex, 0, 0, 0};
// 각 집합 별 정점의 수와 간선의 수를 저장
Map<Integer, Info> m = new HashMap<>();
for (int[] e : edges) {
int od = e[0];
int id = e[1];
if (od == startVertex) continue;
int root = find(od, unionArr);
if (!m.containsKey(root)) {
m.put(root, new Info());
}
Info info = m.get(root);
info.set.add(od);
info.set.add(id);
info.cnt++;
}
// 모든 집합들의 정보를 통해 그래프의 수를 종합한다.
for (int key : m.keySet()) {
Info info = m.get(key);
int vCnt = info.set.size();
int eCnt = info.cnt;
if ((vCnt - eCnt) == 0) {
answer[1]++;
} else if ((vCnt - eCnt) > 0) {
answer[2]++;
} else {
answer[3]++;
}
}한 가지 예외는 막대 그래프의 겨우 size 가 1인 경우 간선이 존재하지 않아 입력된 간선만으로는 size 가 1인 막대 그래프는 다룰 수 없습니다.
따라서 따로 관리를 해줘야 합니다. 이 때의 조건은 시작 정점을 제외하고 indegree 가 없으며 outdegree 가 없는 정점입니다.
이를 구하기 위해 간선을 통해 모든 정점의 시작 정점을 제외한 indegree 정보를 구한 배열과 outdegree 정보를 구한 배열을 만듭니다.
그리고 위에 언급한 조건에 해당되는 만큼 막대 그래프의 수를 증가시킵니다.
// ods 는 startVertex 를 구할 때 만들걸 재사용
int[] idsNotFromStart = new int[1000005];
for (int i = 0; i < 1000005; i++) {
idsNotFromStart[i] = -1;
}
{
for (int[] e : edges) {
int od = e[0];
int id = e[1];
if (idsNotFromStart[id] == -1) idsNotFromStart[id] = 0;
if (od == startVertex) continue;
idsNotFromStart[id]++;
}
}
for (int i = 0; i < 1000005; i++) {
if (ods[i] == 0 && idsNotFromStart[i] == 0) answer[2]++;
}24/12/15 기준 현재 코드는 유효하지만 간선의 개수와 간선의 최대 크기가 1,000,000 라는 점에서 현재 코드는 TLE 를 발생할 수 있다 생각합니다.
일단 Union Find 를 구현하면서 경로 압축이나 union-by-rank 를 사용하지 않아 간선의 순서에 따라 O(n * m) 의 시간이 사용될 수 있습니다.
Union Find 고도화
union-by-rank
이는 union 시 깊이가 더 깊은 집합 트리 A 가 덜 깊은 집합 트리 B 에 속하게 될 때 A 의 깊이가 더 커지는 문제를 가지고 있습니다.
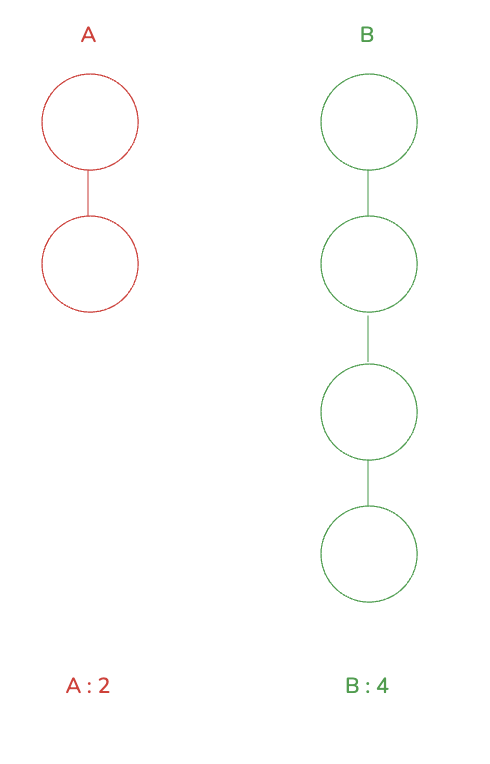
여기서 상대적으로 깊이가 낮은 A 에 B 가 붙을 경우 다음과 같이 A 의 깊이가 5 가 됨을 볼 수 있습니다.
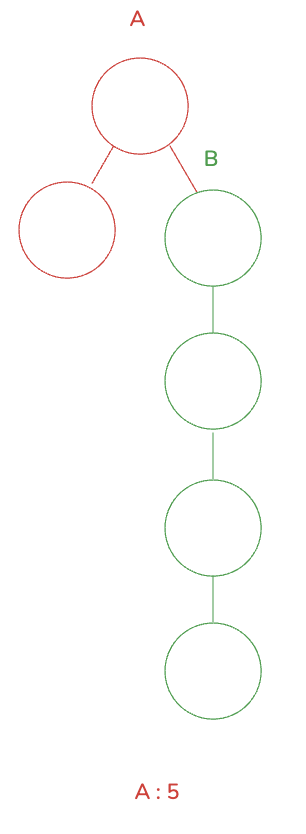
반대로 깊이가 더 깊은 B 에 A 가 붙을 경우 깊이가 4 로 기존 B 의 높이로 유지가 됩니다.
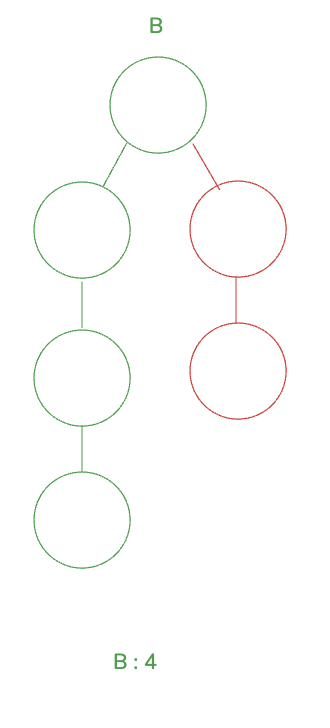
static int[] ranks = new int[1000005];
for (int i = 0; i < 1000005; i++) {
ranks[i] = 1;
}
public static void union(int a, int b, int[] unionArr) {
int aR = find(a, unionArr);
int bR = find(b, unionArr);
if (aR == bR) return;
if (ranks[aR] == ranks[bR]) {
unionArr[aR] = bR;
ranks[bR]++;
} else if (ranks[aR] < ranks[bR]) {
unionArr[aR] =bR;
} else {
unionArr[bR] = aR;
}
}경로 압축
조회 시 모든 경로의 값에 집합의 루트 정점을 적용해 한 번 조회를 한 경우 union 이 적용되지 않았단 가정하에 깊이가 2에서 관리되게 만들어줍니다. 일종의 평탄화
public static int find(int n, int[] unionArr) {
if (unionArr[n] == n) return n;
// 재귀의 기저 케이스로 반환된 루트 정점을 반영합니다.
unionArr[n] = find(unionArr[n], unionArr);
return unionArr[n];
}이렇게 최적화 과정을 거치면 Union Find 는 애커만 함수의 시간복잡도를 가집니다.
상수 시간대로 생각해도 좋을 정도로 상당히 빠른 시간복잡도입니다.
소스 코드
import java.util.*;
class Solution {
static int[] ranks = new int[1000005];
public int[] solution(int[][] edges) {
int startVertex = -1;
int[] ods = new int[1000005];
int[] ids = new int[1000005];
{
for (int[] e : edges) {
int od = e[0];
int id = e[1];
ods[od]++;
ids[id]++;
}
for (int i = 0; i < 1000005; i++) {
if (ods[i] > 1 && ids[i] == 0) startVertex = i;
}
}
int[] unionArr= new int[1000005];
{
for (int i = 0; i < 1000005; i++) {
unionArr[i] = i;
ranks[i] = 1;
}
for (int[] e : edges) {
int od = e[0];
int id = e[1];
if (od == startVertex) continue;
union(od, id, unionArr);
}
}
class Info {
public Set<Integer> set;
public Integer cnt;
public Info() {
set = new HashSet<>();
cnt = 0;
};
}
int[] answer = {startVertex, 0, 0, 0};
// 각 집합 별 정점의 수와 간선의 수를 저장
Map<Integer, Info> m = new HashMap<>();
for (int[] e : edges) {
int od = e[0];
int id = e[1];
if (od == startVertex) continue;
int root = find(od, unionArr);
if (!m.containsKey(root)) {
m.put(root, new Info());
}
Info info = m.get(root);
info.set.add(od);
info.set.add(id);
info.cnt++;
}
for (int key : m.keySet()) {
Info info = m.get(key);
int vCnt = info.set.size();
int eCnt = info.cnt;
if ((vCnt - eCnt) == 0) {
answer[1]++;
} else if ((vCnt - eCnt) > 0) {
answer[2]++;
} else {
answer[3]++;
}
}
int[] idsNotFromStart = new int[1000005];
for (int i = 0; i < 1000005; i++) {
idsNotFromStart[i] = -1;
}
{
for (int[] e : edges) {
int od = e[0];
int id = e[1];
if (idsNotFromStart[id] == -1) idsNotFromStart[id] = 0;
if (od == startVertex) continue;
idsNotFromStart[id]++;
}
}
for (int i = 0; i < 1000005; i++) {
if (ods[i] == 0 && idsNotFromStart[i] == 0) answer[2]++;
}
return answer;
}
public static int find(int n, int[] unionArr) {
if (unionArr[n] == n) return n;
unionArr[n] = find(unionArr[n], unionArr);
return unionArr[n];
}
public static void union(int a, int b, int[] unionArr) {
int aR = find(a, unionArr);
int bR = find(b, unionArr);
if (aR == bR) return;
if (ranks[aR] == ranks[bR]) {
unionArr[aR] = bR;
ranks[bR]++;
} else if (ranks[aR] < ranks[bR]) {
unionArr[aR] =bR;
} else {
unionArr[bR] = aR;
}
}
}늘 그랬듯 더 좋은 코드는 존재한다.
상호 베타적 집합 관점으로 볼 필요 없이 입력으로 주어진 간선의 정보 만으로 구할 수 있습니다.
각 그래프에는 식별자 정점이 존재합니다. 그러니 이 정점을 제외한 그래프의 다른 정점은 무시해도 됩니다.
도넛 그래프는 식별자가 존재하지 않지만 그 외는 존재합니다.
막대 그래프의 경우 맨 끝에 indegree 가 1 개 이상 존재하고 outdegree 는 존재하지 않는 정점이 유일하게 있습니다. (indegree 는 막대 그래프의 이전 정점 또는 시작 정점이 가능합니다.)
8 그래프는 가운데 indegree 2 개 이상 존재하고 outdegree 로 정확하게 2 개가 존재합니다. (indegree 는 그래프 내의 정점 2 개가 필수적이며 시작 정점이 가능합니다.)
도넛 그래프는 모든 그래프의 수에서 막대 그래프의 수, 8 그래프의 수를 감하면 구할 수 있습니다.
모든 그래프의 수는 시작 정점의 outdegree 수 입니다.
따라서 이 과정에서 필요한 모든 수치들은 간선 정보만으로 구할 수 있습니다.
시작 정점을 구하는 법은 상호 베타적 집합을 사용했을 때와 같습니다.
import java.util.*;
class Solution {
public int[] solution(int[][] edges) {
int MAX = 1000005;
int[] indegrees = new int[MAX];
int[] outdegrees = new int[MAX];
for (int[] e : edges) {
int from = e[0];
int to = e[1];
indegrees[to]++;
outdegrees[from]++;
}
int origin = -1;
int stickCnt = 0;
int eightCnt = 0;
for (int i = 0; i < MAX; i++) {
if (indegrees[i] == 0 && outdegrees[i] >= 2) origin = i;
else if (indegrees[i] >= 1 && outdegrees[i] == 0) stickCnt++;
else if (indegrees[i] >= 2 && outdegrees[i] == 2) eightCnt++;
}
int donutCnt = outdegrees[origin] - stickCnt - eightCnt;
int[] answer = {origin, donutCnt, stickCnt, eightCnt};
return answer;
}
}왜 더 나은 방법을 생각하지 못했을까!
능! 지! 차! 이!
도 있겠지만 조금 더 긍정적이고 건설적으로 생각을 해보겠습니다.
한 번 봤을 때 Union Find 가 너무 적절해보여 이외에는 생각하지 않았습니다.
시야가 넘 좁아졌네요. 코드가 조금 길어졌을 때 더 나은 방법이 있음을 느꼈어야 했을까요?
일단은 문제를 더 잘 이해했으면 좋았을 거 같단 생각이 듭니다. 각 그래프에 식별자 정점이 있다는.. 정말 문제를 잘 이해하기 위해 시간을 투자해야겠습니다. 코드 5분 빨리 작성하겠다고 근시안적인 접근법을 사용하는건 살짝 중요한 상황에선 적절하지 않을 수도 있겠습니다.
하이고 잘하고 싶어라~