문제 설명
Greedy의 대표 문제 중 하나입니다.
검정 선이 미사일의 위치
초록 선이 미사일 격추를 위한 요격 미사일의 경우
주황 선은 수평축입니다.
이 문제를 요약하자면 미사일을 전부 요격하는데 드는 미사일(초록선)을 최소화하자는 문제입니다.
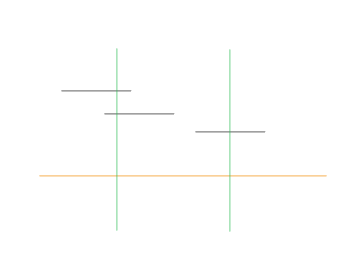
입력
targets
[[4,5],[4,8],[10,14],[11,13],[5,12],[3,7],[1,4]]
제약조건
1 ≤ |targets| ≤ 500,000
targets의 각 행은 [s,e] 형태
이는 한 폭격 미사일의 x 좌표 범위를 나타내며, 개구간 (s, e)에서 요격해야 합니다.
0 ≤ s < e ≤ 100,000,000
접근
어떻게 하면 요격 미사일의 수를 줄일 수 있을까요?
최대한 미사일이 많이 겹쳐진 구간에 요격을 하는 것입니다.
겹쳐진다라는 개념은 다음과 같이 설명할 수 있습니다.
- 일부 구간이 서로 겹친다.
- 한 구간이 다른 구간을 완전히 포함해버린다.
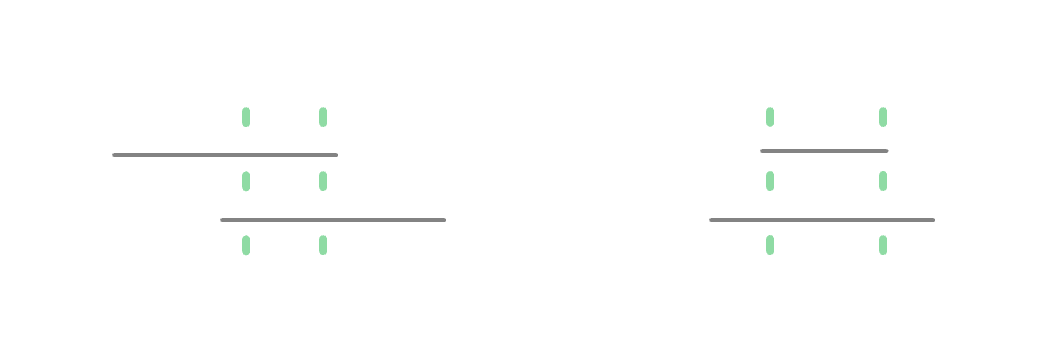
다르게 표현하자면
직선 a의 끝점이 직선 b의 시작점보다 크고
직선 b의 끝점이 직선 a의 시작점보다 커야합니다.
이러한 관점에서 정렬을 통해 더 효율적으로 겹치는 구간을 구할 수 있습니다.
시작점이나 끝점을 기준으로 정렬을 진행하여 할 수 있는데
끝점을 정렬하여 접근해보겠습니다.
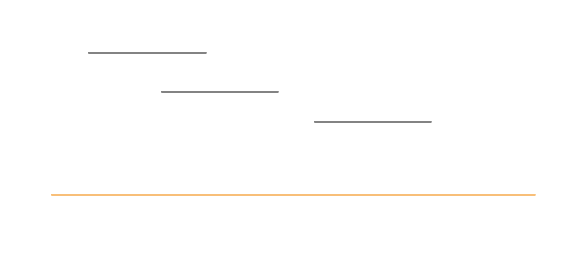
이제 끝점이 작은 구간부터 순차적으로 접근할 수 있습니다. 이러한 정렬로 인해 다음 구간의 끝점이 현재 구간의 시작점보다 반드시 크다는 보장을 받게 되었습니다. 그렇다면 이제 현재 구간의 끝점이 다음 구간의 시작점보다 큰지에 따라 겹침 여부를 알 수 있겠습니다.
정리하자면 최소한의 수를 구하기 위해선 겹침을 유도해야하고 겹침을 알아내기 위해선 두 가지 조건이 맞아야합니다. 이렇게 접근하면 문제를 해결할 수 있습니다.
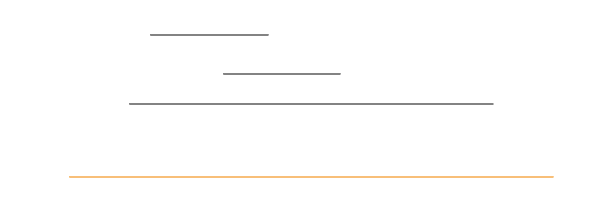
한 가지 마음에 걸리는건 위의 사진의 경우 오해하기가 좋습니다. 사진만 봐선 정렬되었는지를 알 수 없습니다.
코드 내에선 1차원 정렬 내에서 순서로 나타내기에 상관없지만 이러한 사진으로는 오해사기가 쉽습니다.
따라서 끝점이 작을 수록 상단에 존재하도록 그리는게 좋을 것 같습니다.
구현 코드
def solution(targets):
answer = 0
targets.sort(key=lambda x: x[1])
i = 0
while i < len(targets):
answer += 1
tEnd = targets[i][1]
while i < len(targets) and targets[i][0] < tEnd:
i += 1
return answer