최대 연속 부분 구간으로 배우는 PS 사고법

Brute Force

최대 연속 부분 구간을 구하는 문제가 있습니다.

nums = { -3, -2, 1, 2, 3, -4, -5 } 라는 배열이 주어졌을 때
최대 연속 부분 구간은 합 6의 {1, 2, 3} 이 될 것입니다.

구하는 방식에는 어떤게 있을까요?

저는 가장 기본적으로 2 중 For문으로 모든 경우를 비교하면 어떨까 생각했습니다.
그리고 이외의 방법은 없을 것이다 몰래 확언을 했습니다.
일반적으로는 그게 맞다고 생각했습니다.

ans = -float("inf")
for i in range(len(nums)):
	sum = 0
	for j in range(i, len(nums)):
    	sum += nums[j]
        ans = max(ans, sum)

시간복잡도는 O(N^2) 공간복잡도는 O(1) 이 됩니다.

하지만 다른 방법이 있네요. 그것도 성능이 개선된..

Devide and Conquer

여기서 subproblem으로 나누는 경험을 하게 됩니다.
이 문제는 어떻게 더 작은 문제로 나눌 수 있을까요?

최대 연속 부분 구간

이 문장에서 어떤 걸 캐치할 수 있을까요. 유동적인 범위를 가진 부분 구간을 보겠습니다.

현재 문제는 시작 인덱스부터 끝 인덱스까지 모든 원소를 보고있습니다. 이 구간의 범위를 최대한 나눌 수 없는 1까지 만들어보겠습니다. 이 때의 비용은 어떻게 될까요? O(lgN) 의 시간복잡도를 가집니다. merge sort, binary search 의 접근과 비슷합니다.

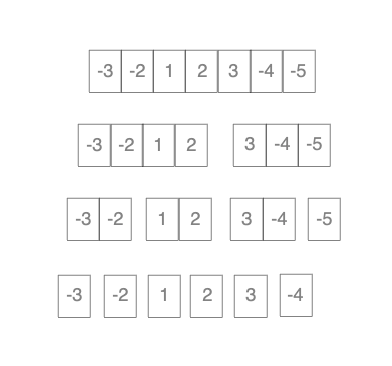
이렇게 나눈 부분 구간들에게 부분 구간의 그리디적 직관을 더합니다.
중간을 기준으로 좌측과 우측을 따로 순회합니다. 그 과정에서 연속적으로 가장 큰 좌측 부분 구간과 우측 부분 구간을 찾아 더하면 그 부분 구간에서의 최대값이 됩니다.

모든 부분 구간에서 최대값을 구했으니 이 값을 비교하면 정답을 구할 수 있습니다.

INF = -float("inf")

def rec(nums, st, ls):
	if st == ls: return nums[st]
    mid = (st + ls) // 2
    tSum = 0
    mxLSum = INF
    for i in range(mid, st - 1, -1):
    	tSum += nums[i]
        mxLSum = max(mxLSum, tSum)
        tSum = 0
    mxRSum = INF
    for i in range(mid + 1, ls):
    	tSum += nums[i]
        mxRSum = max(mxRSum, tSum)
    return max((mxLSum + mxRSum), rec(nums, st, mid), rec(nums, mid + 1, ls)    	

시간복잡도 O(N*lgN) 공간복잡도는 재귀함수에 사용된 스택공간을 의식해야겠지만 O(1)로 생각하겠습니다.
이 풀이를 보고 참 놀랬네요.

DP? Greedy?

하지만 시간복잡도 O(N) 의 더 재밌는 알고리즘이 있습니다.
DP를 사용합니다. 살짝 그리디 가기도..

연결 부분 구간이니 첫 원소부터 연속적으로 결합시키며 결합의 합이 0 이하라면
없느니만 못하니 지금까지의 연결은 무시하고 다시 시작합니다.

ans = MIN
sum = 0
for i in nums:
	sum = max(0, sum + i)
    ans = max(ans, sum)
return ans

---

평범히 생각하면 첫 번째 방법밖에 못 또올렸을것 같은데 두 번째 풀이는 정말 환상적인것 같습니다.