[자료구조] 재귀 함수

재귀 함수란?

---

• 자기 자신을 호출하는 함수

장점

• 반복문에 비해 코드가 간결하고 수정이 용이함

• 변수를 여러개 사용할 필요가 없음

단점

• 코드의 흐름을 직관적으로 파악하기 어려움

• 반복하여 메서드를 호출하기에 지역변수, 매개변수, 반환값을 process stack에 저장하여 메모리를 더 많이 사용

• 메서드를 호출하고 메서드가 종료된 이후에 복귀를 위한 컨텍스트 스위칭 비용이 발생

조건

• 문제의 크기를 작은 단위로 쪼갤 수 있어야 함

• 재귀 호출이 종료되는 시점이 존재해야 함

  • 그렇지 않으면 무한 루프로 인한 스택오버플로우 발생

재귀 함수를 쉽게 이해하는 방법

---

• 점화식을 작성해보기

• 베이스 조건을 작성하여 기초값을 명시해주기

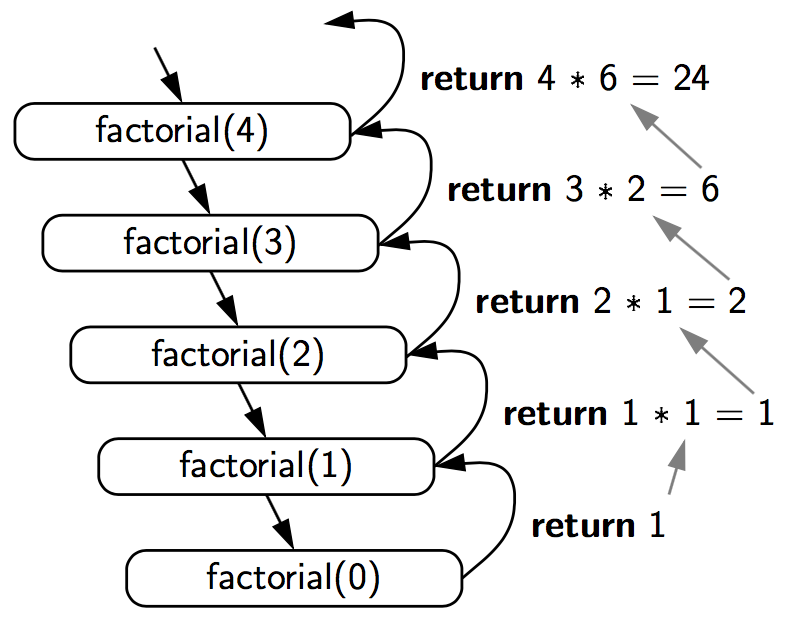
팩토리얼 구하기
f(x) = 1			if(x = 0)
     = x * f(x - 1) if(x >= 1)

• 해당 점화식을 바탕으로 재귀함수를 만들면 다음과 같음

public int Factorial(int num) {
  if(num == 0) {
    return 1;
  }
  return num * Factorial(num - 1);
}

피보나치 수의 경우
f(x) = 0				if(x = 0)
	 = 1				if(x = 1)
     = f(x-1) + f(x-2)	if(x > 1)

• 해당 점화식을 바탕으로 재귀함수를 만들면 다음과 같음

public int fibonacci(int num){
	// base case
	if(num == 0) return 0;
	if(num == 1) return 1;
    // recursive case
    return fibonacci(num - 1) + fibonacci(num - 2);
}

결론

재귀함수를 구현하기 위해서는 점화식을 세워 BaseCase와 Recursive Case를 나눠서 생각해보면 쉽게 이해할 수 있다.