[코딩테스트] 동전 교환 (DP)

문제

다음과 같이 여러 단위의 동전들이 주어져 있을때 거스름돈을 가장 적은 수의 동전으로 교환해주려면 어떻게 주면 되는가?
각 단위의 동전은 무한정 쓸 수 있다.

입력

첫 번째 줄에는 동전의 종류개수 N(1<=N<=50)이 주어진다.
두 번째 줄에는 N개의 동전의 종류가 주어지고, 그 다음줄에 거슬러 줄 금액 M(1<=M<=500)이 주어진다.

각 동전의 종류는 100원을 넘지 않는다.

출력

첫 번째 줄에 거슬러 줄 동전의 최소개수를 출력한다.

예시 입력 1

3
1 2 5
15

예시 출력 1

3

생각

• 이전에 BFS로 동일한 문제를 푼 적이 있었다: BFS를 사용한 동전 교환 문제 풀이 하지만 BFS로 문제를 풀면 중복이 지나치게 많이 일어나기 때문에 M이 클 수록 계산 시간이 많이 걸린다(타임 아웃이 날 수 있다)
• 그래서 DP로 동일한 문제를 다르게 풀어보았다!

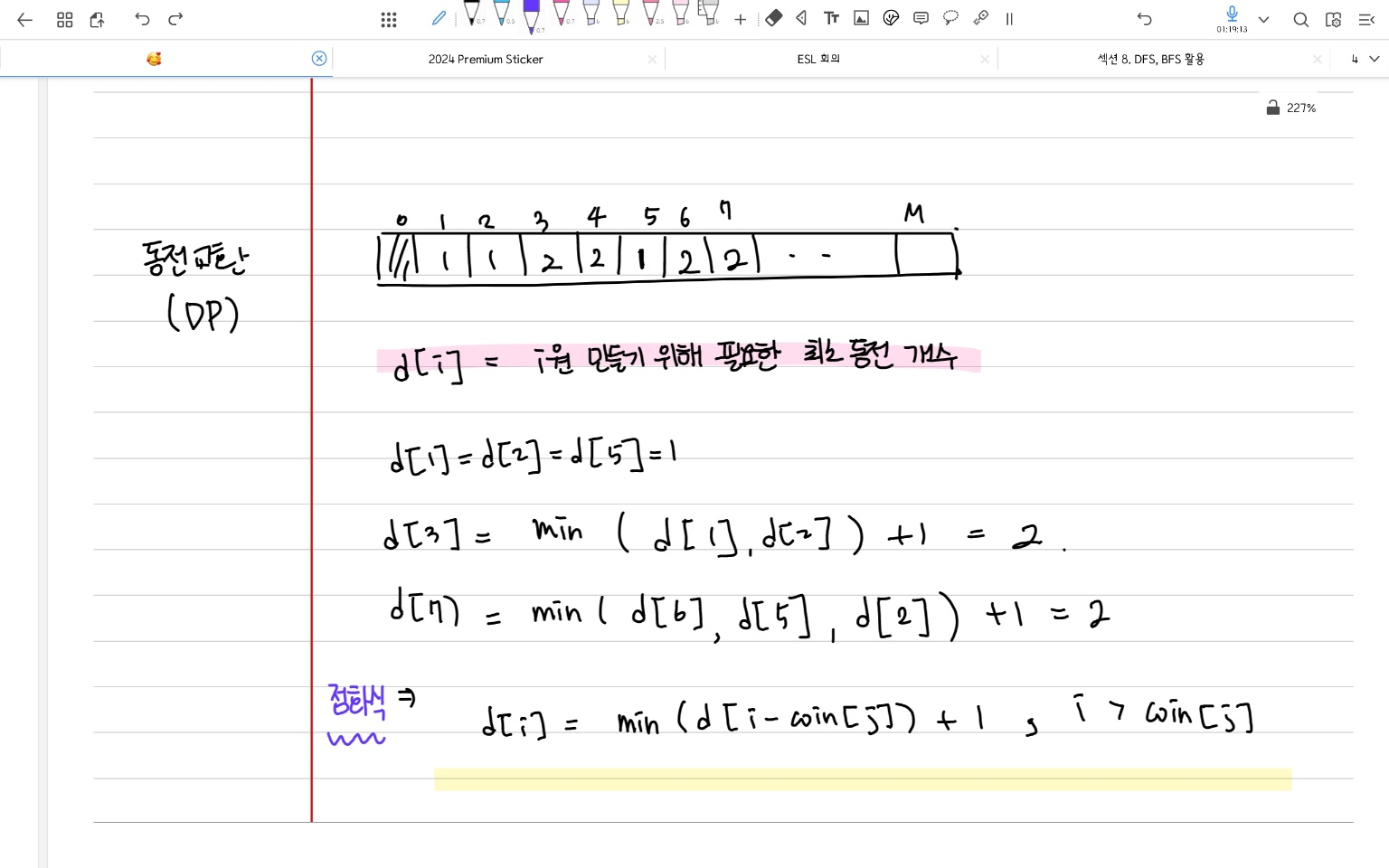
• d[i] = i원을 만들기 위해 필요한 최소 동전의 개수
• d[i원 - 동전 타입 1의 가격], d[i원 - 동전 타입 2의 가격], .. 중 가장 작은 값에다가 1을 더하면 i원을 만들기 위해 필요한 최소 동전의 개수가 된다 (min(d[i-coin[j]) + 1)

코드

import java.util.Arrays;
import java.util.Scanner;

public class ExchangeCoin {

    static int N;
    static int[] coin;
    static int[] d;

    public int dp(int M) {

        Arrays.fill(d, Integer.MAX_VALUE);

        for (int c : coin)
            d[c] = 1;

        for (int i = 1; i <= M; i++) {
            for (int j = 0; j < N; j++) {
                if (i > coin[j]) {
                    d[i] = Math.min(d[i], d[i - coin[j]] + 1);
                }
            }
        }
        return d[M];

    }

    public static void main(String[] args) {
        ExchangeCoin T = new ExchangeCoin();
        Scanner kb = new Scanner(System.in);

        N = kb.nextInt();
        coin = new int[N];

        for (int i = 0; i < N; i++) {
            coin[i] = kb.nextInt();
        }

        int M = kb.nextInt();
        d = new int[M + 1];

        System.out.println(T.dp(M));

        kb.close();
    }
}

• 또한 위 결과를 보면 배열의 크기를 이미 M으로 할당하고, 고정된 배열 사이즈를 사용하여 답을 구하기 때문에 테스트 케이스의 메모리 사용량이 다 일정한 것을 확인할 수 있었다

• 주어진 문제의 크기가 클 경우에는 DP 방식으로 풀 수 있는지를 먼저 확인해 봐야겠다 😀

문제 출처